机器学习之聚类算法——K-Means算法

Posted 2021-04-08 AI深入浅出

欢迎观临AI驿站～愿分享 共成长

前面的算法中的一个显著特征就是我的训练数据中包含了标签，训练出的模型可以对其他未知数据预测标签。在下面的算法中，训练数据都是不含标签的，而算法的目的则是通过训练，推测出这些数据的标签。这类算法有一个统称，即无监督算法(前面有标签的数据的算法则是有监督算法)。无监督算法中最典型的代表就是聚类算法。

让我们还是拿一个二维的数据来说，某一个数据包含两个特征。我希望通过聚类算法，给他们中不同的种类打上标签，我该怎么做呢？简单来说，聚类算法就是计算种群中的距离，根据距离的远近将数据划分为多个族群。

聚类算法中最典型的代表就是K-Means算法。

What is Clustering?
Clustering can be considered the most important unsupervised learning problem; so, as every other problem of this kind, it deals with finding a structure in a collection of unlabeled data.
A loose definition of clustering could be “the process of organizing objects into groups whose members are similar in some way”.
A cluster is therefore a collection of objects which are “similar” between them and are “dissimilar” to the objects belonging to other clusters.
We can show this with a simple graphical example:

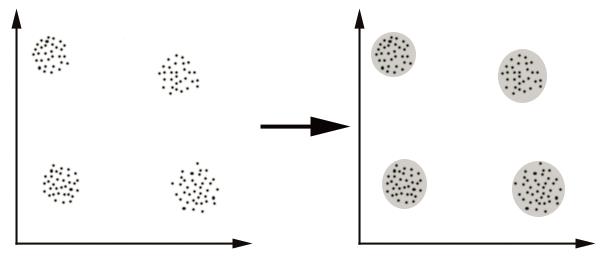
K-Means算法

k-means算法是一种简单的迭代型聚类算法，采用距离作为相似性指标，从而发现给定数据集中的K个类，且每个类的中心是根据类中所有值的均值得到，每个类用聚类中心来描述。

对于给定的一个包含n个d维数据点的数据集X以及要分得的类别K,选取欧式距离作为相似度指标，聚类目标是使得各类的聚类平方和最小，即最小化：

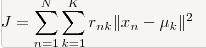
结合最小二乘法和拉格朗日原理，聚类中心为对应类别中各数据点的平均值，同时为了使得算法收敛，在迭代过程中，应使最终的聚类中心尽可能的不变。

算法流程

K-Means算法的具体步骤：

1、选定K个对象作为初始中心，每个对象代表一个聚类中心。这个过程通常是针对具体的问题有一些启发式的选取方法，或者大多数情况下采用随机选取的办法。因为前面说过 k-means 并不能保证全局最优，而是否能收敛到全局最优解其实和初值的选取有很大的关系，所以有时候我们会多次选取初值跑 k-means ，并取其中最好的一次结果。

2、将每个数据点归类到离它最近的那个中心点所代表的 cluster 中，可以通过欧式距离、曼哈顿距离或其他计算。

3、计算出每个 cluster 的新的中心点：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值。

4、判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回第二步。

如何评价一个聚类结果呢？我们计算所有观测点距离它对应的聚类中心的距离的平方和即可，我们称这个评价函数为evaluate(C)。它越小，说明聚类越好。

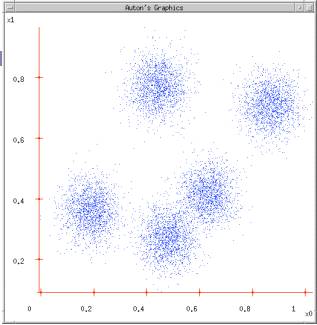
数据集

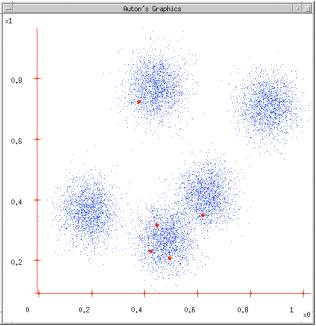
根据K = 5初始化聚类中心，保证聚类中心在数据空间内

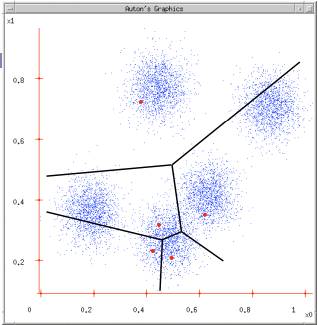
数据划分:根据计算类内对象和聚类中心之间的相似度指标

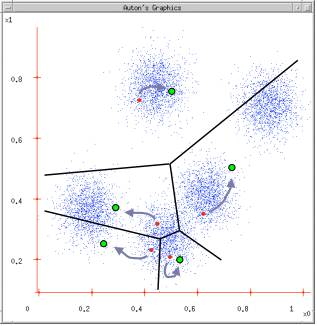
将类内之间数据的均值作为聚类中心，更新聚类中心

问题及方案

K-means算法非常简单，然而却也有许多问题。

1）首先，算法只能找到局部最优的聚类，而不是全局最优的聚类。而且算法的结果非常依赖于初始随机选择的聚类中心的位置。我们通过多次运行算法，使用不同的随机生成的聚类中心点运行算法，然后对各自结果C通过evaluate(C)函数进行评估，选择多次结果中evaluate(C)值最小的那一个。

2）关于初始k值选择的问题。首先的想法是，从一个起始值开始，到一个最大值，每一个值运行k-means算法聚类，通过一个评价函数计算出最好的一次聚类结果，这个k就是最优的k。我们首先想到了上面用到的evaluate(C)。然而，k越大，聚类中心越多，显然每个观测点距离其中心的距离的平方和会越小，这在实践中也得到了验证。第四节中的实验结果分析中将详细讨论这个问题。

3）关于性能问题。原始的算法，每一次迭代都要计算每一个观测点与所有聚类中心的距离。有没有方法能够提高效率呢？是有的，可以使用k-d tree或者ball tree这种数据结构来提高算法的效率。特定条件下，对于一定区域内的观测点，无需遍历每一个观测点，就可以把这个区域内所有的点放到距离最近的一个聚类中去。