数学建模算法学习之K-means聚类算法（建议收藏）

Posted 2021-08-07 数模乐园

K-means聚类算法

聚类是指将数据划分成多个组的任务，每一个组都叫做簇。聚类的目标就是要划分数据，使得每一个组里面的元素非常相似，但不同组里面的数据又非常不同，简单来说就是叫分类。我们通过聚类可以很方便地让我们对数据进行处理，把相似的数据分成一类，从而可以使得数据更加清晰。

K-means是聚类算法中最典型的一个，也是最简单、最常用的一个算法之一。这个算法主要的作用是将相似的样本自动归到一个类别中。通过设定合理的K KK值，能够决定不一样的聚类效果。

K-means算法原理与理解

01

基本原理

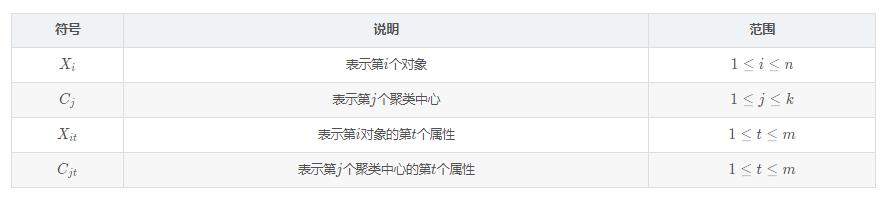
假定给定数据样本X ，包含了n 个对象

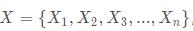
其中每个对象都具有m个维度的属性。Kmeans算法的目标是将n个对象依据对象间的相似性聚集到指定的k个类簇中，且每个对象到类簇中心距离最小。

02

算法流程

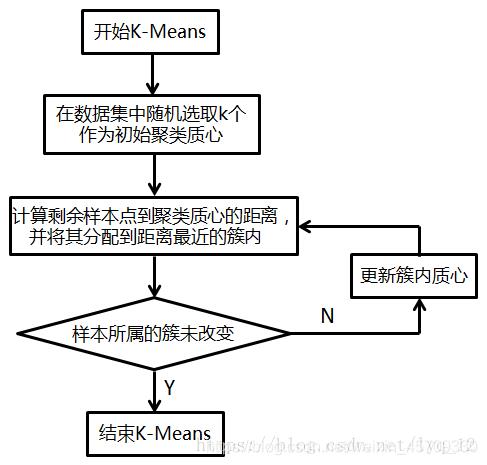
主要思想：在给定k值和k个初始类簇中心点的情况下，把每个点分到离最近的类簇中心点所代表的类簇中，所有点分配完毕之后，根据一个类簇内所有点的到类簇中心的距离的平均值，然后多次迭代进行点的分配和类簇中心点的更新。

那么，我们首先初始化k个聚类中心

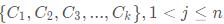
然后计算每一个对象到每一个聚类中心的欧氏距离

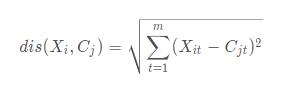
03

算法步骤

输入：样本集D，簇的数目k，最大迭代次数N；

输出：簇划分（k个簇，使平方误差最小）；

算法步骤：

（1）为每个聚类选择一个初始聚类中心；

（2）将样本集按照最小距离原则分配到最邻近聚类；

（3）使用每个聚类的样本均值更新聚类中心；

（4）重复步骤（2）、（3），直到聚类中心不再发生变化；

（5）输出最终的聚类中心和k个簇划分；

04

K-Means算法优缺点

优点
（1）原理易懂、易于实现；
（2）当簇间的区别较明显时，聚类效果较好；

缺点
（1）当样本集规模大时，收敛速度会变慢；
（2）对孤立点数据敏感，少量噪声就会对平均值造成较大影响；
（3）k的取值十分关键，对不同数据集，k选择没有参考性，需要大量实验

05

代码实现

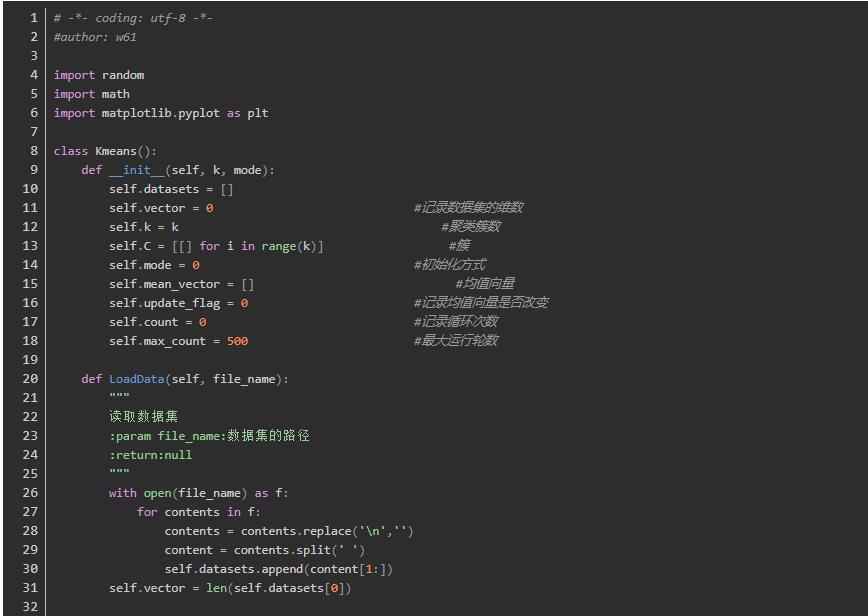
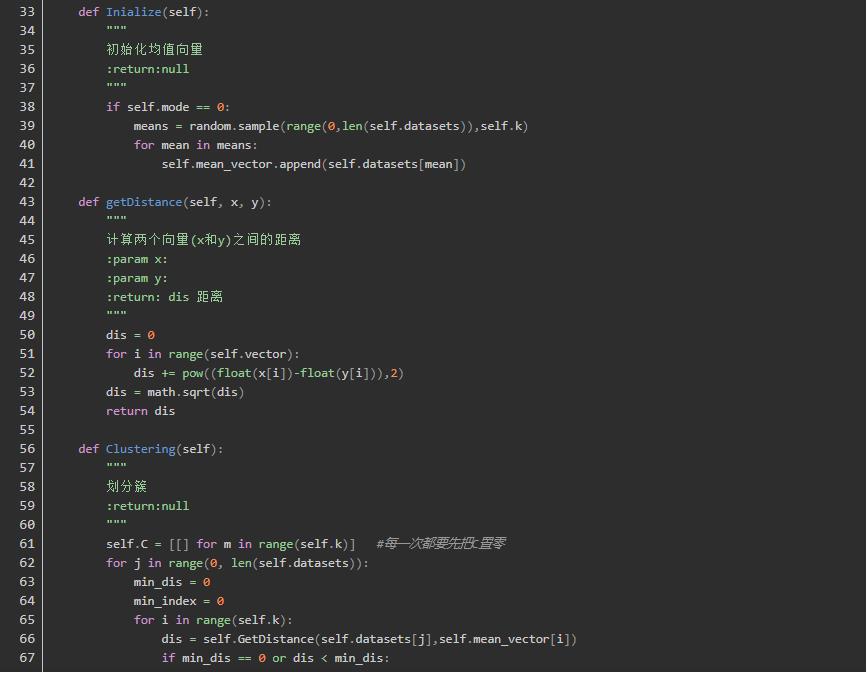
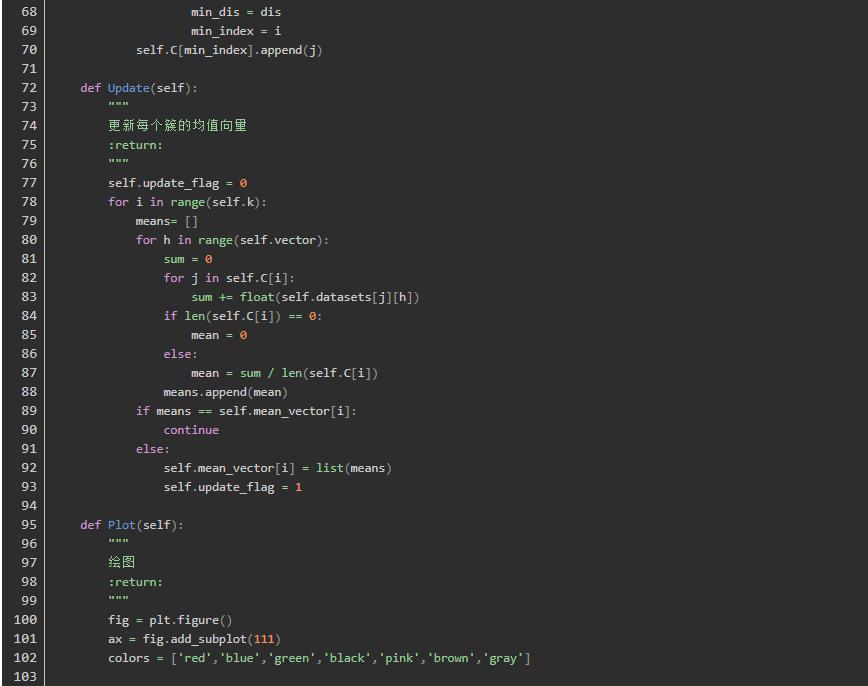
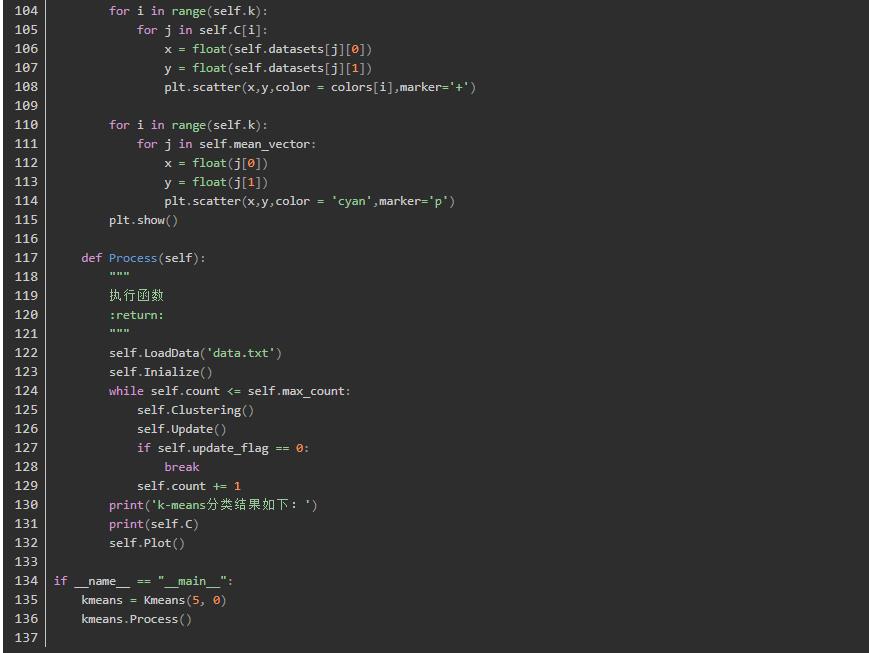
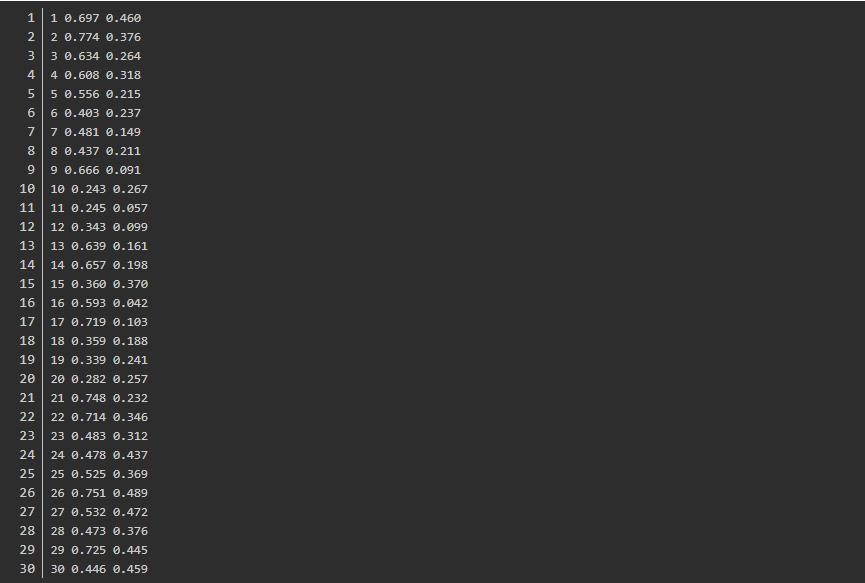
测试所用的数据

来源：CSDN

仅用于学术分享，版权属于原作者

“数模乐园”b站官方账号现已开通

大家可以在b站搜索数模乐园，观看“国赛专题讲座”

点击图片跳转，视频已上传b站，欢迎大家来学习

b站链接：https://www.bilibili.com/video/BV16o4y1Q7sc?share_source=copy_web

也可点击原文链接直接跳转

从“数模乐园”微信公众号菜单栏可直接添加

“数乐君”微信

添加后回复关键词【课件】

领取即可