使用启发式机器学习的方法进行流量预测

Posted 2021-04-03 山坡水文土壤前沿瞭望

学术简报

题目：Streamflow forecasting using heuristic machine learning methods

期刊/DOI:ResearchGate/

10.1109/ICCIS49240.2020.9257658

 01 

摘要

  流量预测对水资源系统的设计和管理至关重要。本研究利用Neelum和Kunhar河月径流数据，对人工神经网络遗传算法(ANN-GA)和自适应神经模糊推理系统-遗传算法(ANFIS-GA)两种启发式方法在径流预报中的精度进行了评价。利用统计指标检验了两种方法的预测能力，并与 M5回归树(M5RT)模型进行了比较。结果表明，ANN-GA 和 ANFIS-GA 比 M5RT 模型具有更高的预测精度。月数的增加表明周期性对模型预测精度有正向影响。

 02 

方法

A.混合人工神经网络-遗传算法(ANN-GA)模型

简单ANN模型的应用存在着（i）训练周期长、（ii）局部收敛而非全局最优解、（iii）参数数量大等缺点。因此，将遗传算法(GA)与人工神经网络(ANN)相结合的进化算法就是克服这些缺点，提高ANN性能的有效方法。图1展示了在本研究中实施的混合ANN-GA模型，用于Kunhar和Neelum河的月径流预报。遗传算法的参数选择(染色体初始种群的随机生成，每条染色体适应度函数的评价)，交叉，变异通过试错过程(图1)确定。近二十年来，混合ANN-GA模型在各个工程领域得到了广泛的应用。

全世界1/5的陆地为山地，分布在130多个国家和地区，1/10的人口生存在山地。山区提供了人类发展50%以上的物质文化需求，世界50%的人口直接或间接依赖山区而生存。我国是世界上最大的山地国家，山区占我国国土面积的近七成。我国山区人口占全国人口的一半以上，占全国农业人口的78%左右。

图1 混合ANN-GA模型的体系结构

B.混合自适应神经模糊推理系统-遗传算法(ANFIS-GA)模型

为了解决复杂问题，适当的集成人工智能系统是至关重要的。本研究采用混合自适应神经模糊推理系统(ANFIS)与遗传算法(ANFIS-GA)优化Kunhar和Neelum河的月径流预报。在图2中，混合 ANFIS-GA模型的结构由五个层次组成(即第一层: 输入层，第二层: 模糊化层，第三层: 规则层，第四层: 标准化层，第五层: 解模糊化层)。Jang将ANN和模糊推理系统(FIS)集成在一个框架中，利用两种技术的优点，提出了ANFIS的概念。IF-THEN 规则用于解释输入和输出变量之间的关系。最近，ANFIS-GA 模型在科学和工程领域得到了广泛的应用。

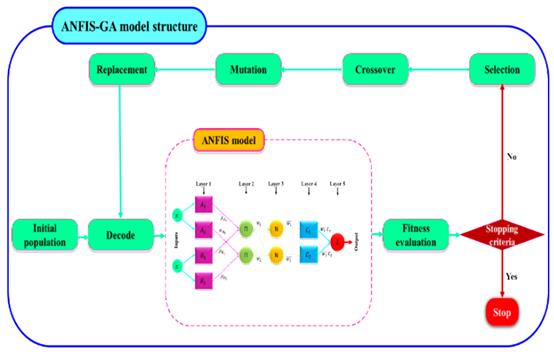
图2 典型混合ANFISA-GA模型

C.M5回归树（M5RT）模型

为了解决复杂问题，Quinlan { Formatting Citation }首次提出了M5回归树(M5RT)模型的概念，这是一个依赖于二进制决策框架的层次模型。它利用末端(叶)节点的线性回归原理，通过将参数空间拆分成子空间，构造出输入和输出参数之间的线性关系（图3）。M5RT 模型的生成需要经过两阶段：(i)第一阶段首先将输入/输出数据分解成子集，然后基于标准差缩减(SDR)建立决策树，(ii)第二阶段通过拟合线性回归函数{Formatting Citation}修剪过生长的树木(样本)。SDR使用以下表达式计算:

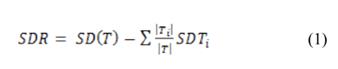
其中，T=到达节点的实例集，T_i= 具有该势集的第 i 个结果的示例子集，和SD = 标准差。目前，M5RT模型已经在工程水文学中得到了实际应用。

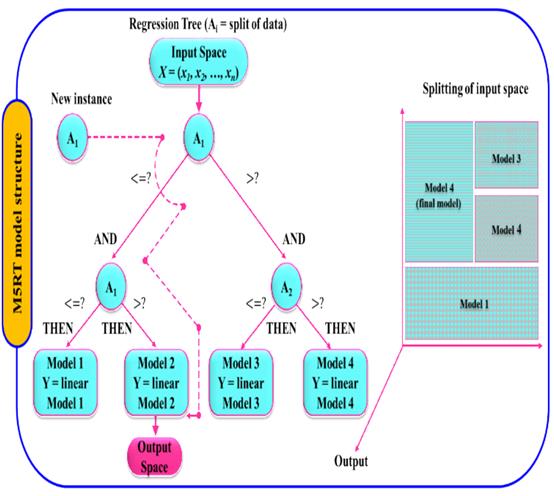
图3 案例研究范围及表现指标

在本研究中，使用了从Kunhar和Neelum获得的每月河流流量数据(图4)。表1总结了有关流量统计特性的简要信息。从表格中可以看出，Neelum河的水量比Kunhar河的水量要大(请参阅表格中提供的流量范围和偏度系数)。从表中还可以看出，在训练/验证阶段，流量的最小值高于测试阶段。这可能会给模型在试验阶段捕捉低流量带来困难。以前的流量值作为三种方法的输入，并考察了周期分量(输出月份数)的影响。应用统计学和测定系数(R2)评价所采用的方法。

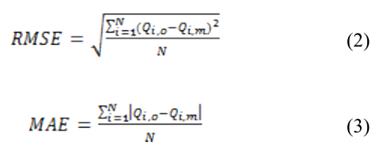
其中N是数据的个数，Q_i,o是观测到的流量，是模拟的流量。

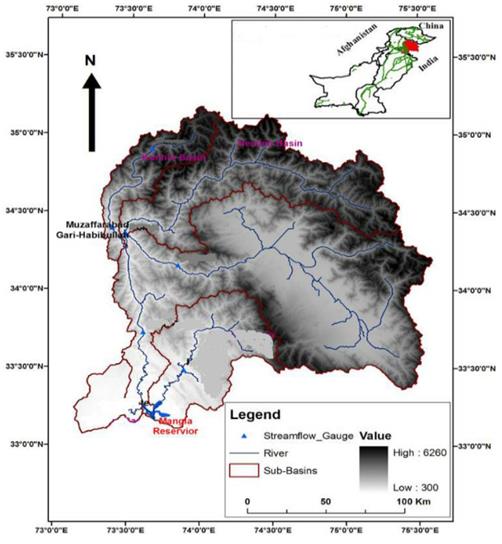
图4 Neelum和Neelum的位置图

 03 

结果与讨论

本文研究了ANN-GA、ANFIS-GA和M5RT三种模型在径流预报中的应用。在应用三种方法之前，将数据分为训练、验证和测试三部分。采用相同的进化算法(GA)对ANN模型和ANFIS模型进行校正，考察两者的效率差异。应用方法的验证和试验结果见表2。从表中可以看出，我们使用了包括1至3个滞后的流量输入，并且将周期值(α)加入到第三个输入组合中，以观察其对模型效率的影响。

表1 Neelum和Neelum的月径流量

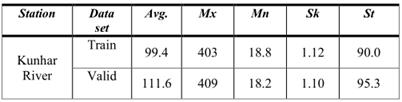
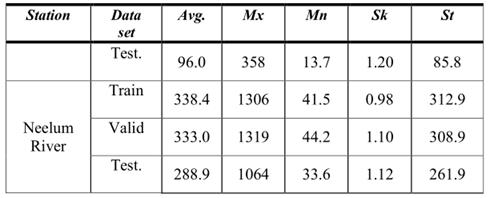
Avg，Mx，Mn，Sk 和 St 分别表示平均值，最大值，最小值，偏斜系数和标准差。

从表2可以明显看出，具有三种流量和周期性输入的ANN-GA (RMSE: 31.16 m³/s，MAE:18.67 m³/s 和 R2:0.891)和ANFIS-GA(RMSE: 30.57 m³/s，MAE: 19.99 m³/s 和 R2:0.884)具有几乎相同的精度，并且它们的性能优于M5RT模型(RMSE: 40.73 m³/s，MAE: 25.18 m³/s 和 R2:0.821)。M5RT模型的精度较低，应该是该模型采用的线性结构。从表中可以看出，ANN和ANFIS 方法的周期性在一定程度上提高了模型的效率，例如 ANN-GA的RMSE 从34.37 m³/s 提高到31.16 m³/s，ANFIS-GA从34.70 m³/s 提高到30.57 m³/s。

表2不同流量下ANN-GA、ANFIS-GA和M5RT模型的RMSE、MAE和R²统计量——KUNHAR河

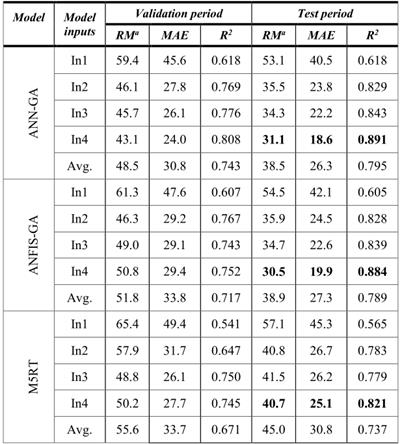
RM表示RMSE

表3列出 Neelum河使用的RMSE、MAE及R²方法的验证及检验统计。结果表明，具有三次流量和周期性输入的最优 ANN-GA 模型性能(RMSE: 114.4 m³/s，MAE: 72.45 m³/s，R²:0.870)优于 ANFIS-GA 模型(RMSE:118.6 m³/s，MAE: 74.01 m³/s，R²:0.837)和 M5RT 模型(RMSE:121.7 m³/s，MAE: 81.07 m³/s，R²:0.821)。

在该站，周期性输入提高了三种模型的精度，例如，ANN-GA的RMSE从120.6 m³/s 提高到114.4 m³/s，对于ANFIS-GA从122.3 m³/s 提高到118.6 m³/s，对于M5RT从137.0 m³/s提高到121.7 m³/s。ANN-GA和ANFIS-GA或ANFIS-GA与M5RT之间的差异对于这条河来说并不太大。对于这条河流可以说M5RT也是一个很好的径流预报替代方案。与ANN和ANFIS相比，该方法的主要优点是能够提供显式方程，便于实际应用。

表3不同河流输入组合下 ANN-GA、 ANFIS-GA 和 M5RT 模型的 RMSE、 MAE 和 R2统计量—— NEELUM 河

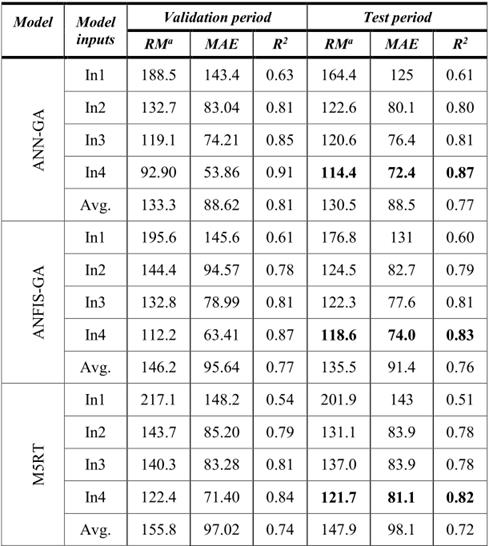
图5比较了Kunhar站模型估计的散点图，从图中可以明显看出，ANN和ANFIS模型都比M5RT模型具有更高的R²，但散点估计较少。图6显示了Neelum站三种机器学习方法观测和估计流量的时间散点图。

从这些数据中可以清楚地看出三种方法之间的差异，并且显然所有的 ANN-GA 和 ANFIS-GA 模型都比 M5RT 模型提供了更好的结果。其原因可能是 M5RT 模型是线性结构，而ANN-GA、ANFIS-GA 启发式模型捕捉非线性现象的能力较强。

另一个需要考虑的问题是 ANN-GA 和 ANFIS-GA 的学习过程比 M5RT 需要更多的时间和更多的内存，且它们没有明确的方程，这使得 M5RT 更有利于实际应用。ANFIS-GA与 ANN-GA 相比，其结构复杂、需要标定的参数多、训练时间长等。因此，后一种方法在实践中可能是首选的。

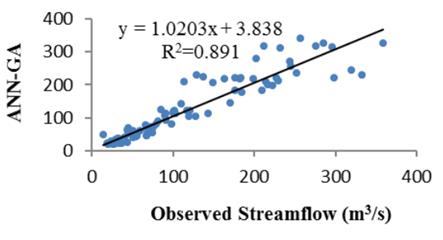
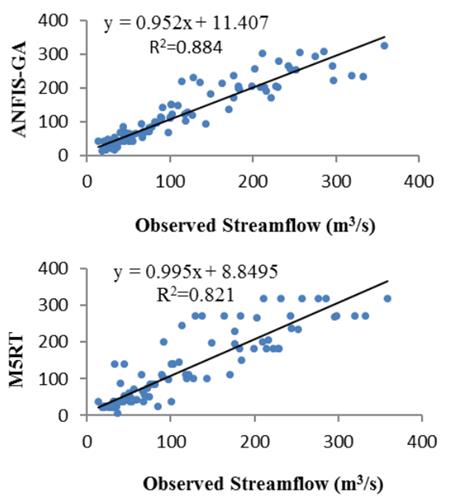
图5用 ANN-GA、ANFIS-GA和 M5RT 对Kunhar河试验期的河流流量进行了观测和预报

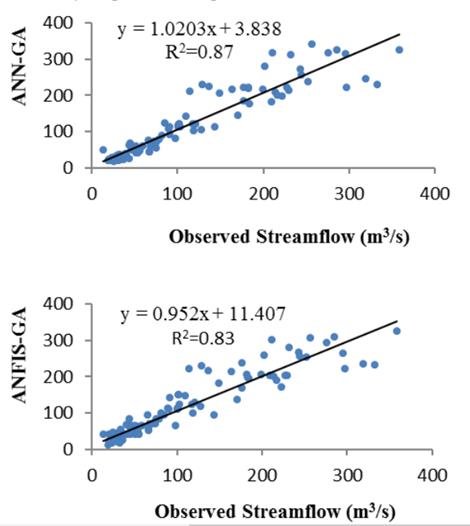
图6用 ANN-GA、 ANFIS-GA 和 M5RT 对Neelum河试验期的河流流量进行了观测和预报

 04 

结论

本文研究了ANN-GA和ANFIS-GA两种启发式方法对 Neelum 和Kunhar河流域月径流量的预测能力，并与传统线性模型 M5Tree进行了比较。采用四种不同的时间滞后输入组合(包括月数)对 ANN-GA、 ANFIS-GA 和 M5RT 模型进行了评估，以观察周期性对预测精度的影响。结果表明，两种启发式模型 ANFIS-GA 和 ANN-GA 都比 M5RT 模型提供了更准确的结果。研究还发现，周期性提高了模型的预测精度。在本研究中，只使用以前的流量值作为输入来预测流量。然而，对于未来的研究，除了流量值之外，还可以利用降水、温度和其他气象要素来预测流量。

 05 

参考文献

[1]Rezakazemi, M.; Dashti, A.; Asghari, M.; Shirazian, S. H2-selective mixedmatrix membranes modeling using ANFIS, PSO-ANFIS, GA-ANFIS. InternationalJournal of Hydrogen Energy 2017, 42, 15211-15225, doi:10.1016/j.ijhydene.2017.04.044.

[2]Yaghoubi, B.; Hosseini, S.A.; Nazif, S. Monthly prediction of streamflowusing data-driven models. Journal of Earth System Science 2019, 128,doi:10.1007/s12040-019-1170-1.

[3]Hadi, SJ, Tombul, M, Monthly streamflow forecasting using continuous  wavelet and  multi-gene  genetic programming combination, Journal of Hydrology, 561, 674–687, 2018.

文案吴沛珊

排版吴沛珊

校核倪飞宇

THE END