机器学习中的贝叶斯方法---先验概率似然函数后验概率的理解及如何使用贝叶斯进行模型预测

Posted 2020-09-07 hapjin

在 机器学习中的贝叶斯方法---先验概率、似然函数、后验概率的理解及如何使用贝叶斯进行模型预测（1） 文章中介绍了先验分布和似然函数，接下来，将重点介绍后验概率，即通过贝叶斯定理，如何根据先验分布和似然函数，求解后验概率。

 

在这篇文章中，我们通过最大化似然函数求得的参数 r 与硬币的抛掷次数(抛掷次数是10，求得的r=0.9)有关，为了更好地描述 参数 r 与 抛掷次数之间的关系，对下面符号作一些说明：

• 参数 r ：抛一次硬币出现正面的概率，显然 r 的取值范围为[0,1]
  
• y_N，在N次抛硬币实验中，出现正面的次数

那么，在N次抛硬币实验中，出现了y_N次正面，r 取何值比较合适呢？---我们就用概率密度p(r|y_N)来描述 参数 r 与 抛掷次数之间的关系。

根据 条件概率公式 和 全概率公式，有：

（公式1）

 根据上一篇文章，在这个公式中，p(r)是先验信息，准确地说应该叫先验概率密度。对于先验信息，有如下三种情况：

• 1：一无所知，我们不知道抛一次硬币出现正面的概率是大于 还是小于 还是等于 出现反面的概率
• 2：抛一次硬币出现正面的概率 等于 出现反面的概率
• 3：抛一次硬币出现正面的概率 大于 出现反面的概率

那么，先验概率密度p(r)如何描述呢？即它服从何种分布呢？这三种情况下的先验概率密度的图形形状如下：

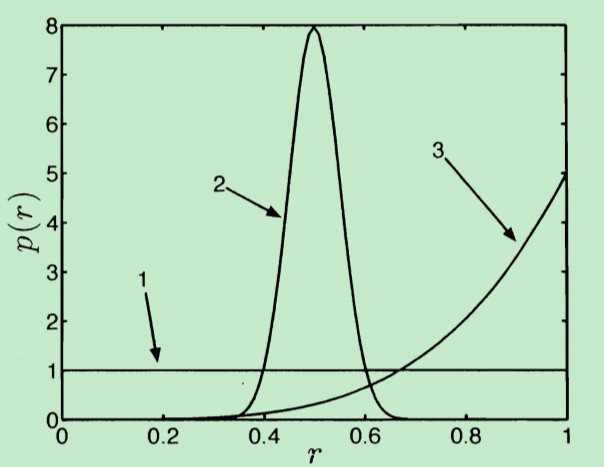
• 第1种情况 p(r)概率密度是均匀分布，因为我们对 r 一无所知，认为 r 在[0,1]范围内取值是等概率的。
• 第2种情况 p(r)表示：抛一次硬币出现正面的概率 等于 出现反面的概率，也即，在 r=0.5 是最可能的。因此在0.5处，概率密度最大。
• 第3种情况：硬币出现正面的概率r 大于 出现反面的概率。概率密度越大，表示 r 越可能取 接近于1的值。

总之，对于上述三种情况而言，它们其实可以统一用beta 分布来表示( beta density function)。beta概率密度带有两个参数α 和 β，它的表达式如下：

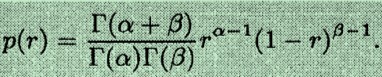
参数α 和 β 决定了beta概率密度的图形形状。在上图中的三个概率密度曲线中：

第一个曲线对应的参数α 和 β，α=1，β=1

第二个曲线对应的参数α 和 β，α=50，β=50

第三个曲线对应的参数α 和 β，α=5，β=1

 

p(y_N|r)是似然函数，它的解释如下：

how likely is it that we would observe our data(in this case, the data is y_N) for a particular value of r

 似然函数用来衡量：已观测到的数据发生的可能性。如果我们的 r 很合适，那么p(y_N|r)就应该很大---最大化似然函数，也表明观测到的数据y_N很合理。

在给定 r 的条件下，抛硬币是一个独立重复实验，故p(y_N|r)服从二项分布。

从上面描述可以看出：似然函数与实验过程中观测到的数据息息相关。下图给出了两个不同抛硬币次数的实验下的似然函数。其中一个抛了100次硬币，出现了70次正面；另一个抛了10次硬币，出现了6次正面。

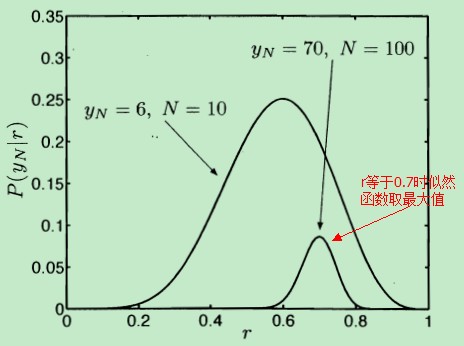
从上图中可以得知：①似然函数不是概率密度函数。因为概率密度函数的积分为1(曲线围成的面积为1)，而上图中两个似然函数曲线围成的面积显然不相等，抛100次出现70次正面的这次实验 所代表的似然函数的参数 r 的取值范围大约为[0.6,0.8]，而抛10次出现6次正面的实验 所代表的似然函数的参数 r 的取值范围约为[0.2,0.9]，其变化范围要大于前者。

这是因为：进行的实验次数越多，我们掌握的信息也就越多，关于先验信息 r 的不确定性也就越小。

根据上面的似然函数的图像，在给定一次实验数据的前提下，比如抛100次硬币，出现了70次正面，我们的目标就是寻找使得似然函数取最大值的r，比如图中的r=0.7

 

p(y_N)是边界似然函数(marginal distribution of y_N)

根据公式：

（公式1）

要想求后验概率p(r|y_N)，还得先求出p(y_N)，而p(y_N)是可由下式获得：

 

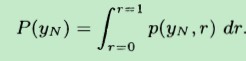
由条件概率公式，有：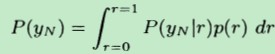

从上式可以看出，(marginal likelihood)边界似然函数p(y_N)，其实还是由似然函数p(y_N|r) 和 先验分布p(r) 来决定。

边界似然函数的作用是用来：选择最合适的先验信息。因为在上面我们讨论了三种先验信息，哪一种先验信息是最合理的呢？使p(y_N)取最大值的先验信息就是最合理的先验信息。

 

p(r|y_N)是后验分布(posterior distribution)

后验分布就是用来对未知数据进行预测的模型，为什么呢？

比如对于抛硬币而言，我们知道它就是一个二项分布B(N,r)，对于二项分布而言，它最重要的参数就是事件发生的概率r，即出现正面的概率r。

在后验分布p(r|y_N)中，我们基于已观测到的数据y_N(训练样本)，求出具体的最合适的模型参数 r^″，因而也就确定了一个具体的二项分布B(N,r^″)。那么对于下一轮试验，比如抛20次硬币，其中有8次正面向上的概率为：

从上面的公式1也可以看出：后验分布 tells us something about how much information we have about r after combing what we knew beforehand(the prior) and what we have seen(the likelihood)

这句话的通俗理解就是：贝叶斯后验分布就是利用，我们在实验前已经掌握了的信息(先验知识)，和做了若干次实验发现的一些规律(似然函数)，确定出合适的二项分布模型参数 r ，然后基于 r 来预测新的实验结果。 

 

这里还有2个疑问没有解决：

• 1，为什么先验分布 服从 beta 分布？
• 2，如何根据公式1 计算后验分布？

对于问题1而言，是概率论里面的一个理论知识：当似然函数服从二项分布时，选择服从beta概率密度函数来表示 先验分布 是一个很好的选择，这样似然函数与先验分布就构成了“共轭”关系。共轭关系的好处就是：不用计算边界似然函数(公式1中的分母)了，从而简化了后验分布p(r|y_N)的计算。

但具体原理我也不懂。

 

由于似然函数是二项分布形式，而我们又选择了Beta分布作为先验分布，根据上图中显示的共轭关系，那么：posterior is the same form as the prior（后验分布与先验分布具有相同的形式，服从相同的分布），也即后验分布也服从Beta分布了。

根据公式1，我们知道：

 

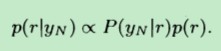
又由于后验分布服从beta分布，因此有：

 

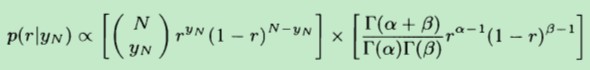
根据维基百科中关于beta分布的解释，beta分布主要由两个参数决定，因为对后验分布进一步简化得到：

 

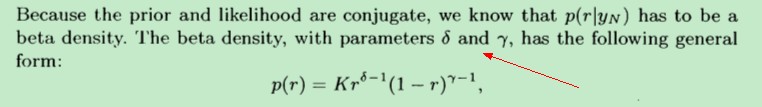
最终，求得的后验分布如下，具体推导过程可参考：《A First Course of Machine Learning》 第三章

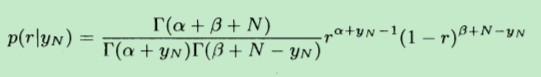
其中，α和β是先验分布中的两个参数，而r是似然函数中的参数，N表示实验的次数，y_N表示事件发生的次数(出现正面的次数)

从而后验分布 完美地 基于先验分布 和 似然函数 表示出来了。

 

现在，我们已经求得了后验分布的表达式，而我们前面提到，对于先验分布而言，一共有三种情况，这三种情况分别对应的α和β参数是不同的，至于采用哪种先验分布的参数α和β，是根据边界似然函数来决定的，这里就不具体介绍了。若想进一步地了解，请参考：《A First Course of Machine Learning》 第三章

 

原文：http://www.cnblogs.com/hapjin/p/6656642.html