采用支持向量回归（SVR）和随机森林回归预测两种机器学习方法对房价进行预测（附完整代码）

Posted 2023-03-09 带我去滑雪

       大家好，我是带我去滑雪，每天教你一个小技巧！  

       本文分别采用支持向量回归（SVR）和随机森林回归预测两种机器学习方法对房价进行预测。随机将数据分为训练集和测试集，比例为8:2，数据和代码均在文末。

1、数据展示

      本文利用Python爬取到的房价信息做数据可视化，爬取数据的文章见：

https://blog.csdn.net/qq_45856698/article/details/129367419?spm=1001.2014.3001.5501

       将x1 （房屋的卧室数量）、x2 （房屋的客厅数量）、x3 （房屋面积）、x4 （房屋装修情况）、x5 （有无电梯）、x6 （房屋所在楼层位置）、x7 （房屋附近有无地铁）、x8 （关注度）、x9 （看房次数）作为特征变量，分别预测y（每平方米价格）和y1 （房屋总价）。

2、支持向量回归（SVR）

2.1 基本原理

       SVR（Support Vector Regression，支持向量回归）在做拟合时采用了支持向量机的思想来对数据进行回归分析。给定训练数据集：

 2.2 支持向量回归（SVR）预测房价

       支持向量机的理论基础（凸二次规划）决定了它最终求得的为全局最优值而不是局部最优值，也保证了它对未知样本的良好泛化能力支持向量机是建立在统计学习理论基础之上的新一代机器学习算法，支持向量机的优势主要体现在解决线性不可分问题，它通过引入核函数，巧妙地解决了在高维空间中的内积运算，从而很好地解决了非线性分类问题。对于核函数的选择，本文分别对RBF核（径向基核）、POLY核（多项式核）、Sigmoid核进行了测试，测试结果发现 RBF核效果最好，故本文选取RBF核作为支持向量机的核函数。

（1）预测y（每平方米价格）

      支持向量回归（SVR）的部分预测结果见表1，模型预测值与真实值的比较见图1，模型的评价指标见表2，代码见附件。

表1 SVR部分预测结果表

真实值	预测值	真实值	预测值	真实值	预测值
43066	42154	33207	30524	32800	31980
25359	28207	53158	34241	25664	28511
41568	46833	34000	27752	25782	35538
26516	32545	46280	42385	39119	31872
36408	46340	23883	31611	50567	46447
59009	43743	23870	31312	30000	40338
47038	47569	47574	29933	30975	32763
51502	63952	74906	71099	28747	32352
40630	35673	58329	43405	30590	37024
38017	48810	56915	37197	42719	49262
28584	52414	24337	37558	30607	30393
58269	37492	41096	27468	28727	34081
22728	25701	25089	29508	53968	50215

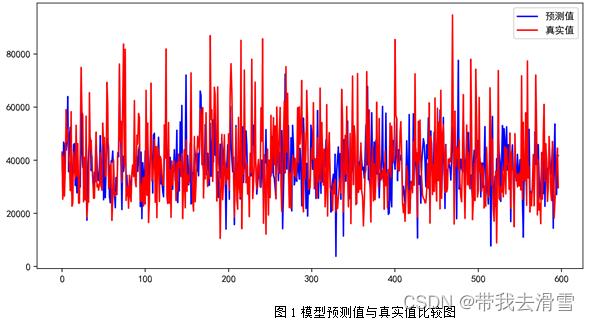
表2 模型预测效果评价指标

	RMSE	MAE
0.7492	14164.27	10469.42

      通过表6-2 可以看到，使用支持向量回归（SVR）预测y（每平方米价格），其预测效果较好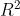，达到了0.7492。 

（2）预测 y1 （房屋总价）

       支持向量回归（SVR）的部分预测结果见表3，模型预测值与真实值的比较见图2，模型的评价指标见表4，代码见附件。

表3 SVR部分预测结果表

真实值	预测值	真实值	预测值	真实值	预测值
230	246	193	183	570	486
350	392	235	257	215	251
175	224	230	292	730	799
750	752	325	366	225	256
769	554	235	248	195	219
508	503	280	301	480	445
880	990	440	357	600	530
258	279	458	238	320	324
460	542	510	471	380	450
328	598	250	150	530	354
315	214	280	286	158	23
200	323	580	392	580	375
152	223	730	566	570	486

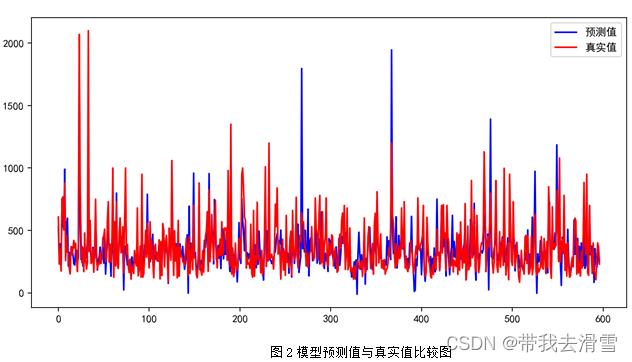
表4 模型预测效果评价指标

	RMSE	MAE
0.4465	172.41	110.89

       通过表4可以看到，使用支持向量回归（SVR）预测 y1 （房屋总价），其预测效果较差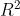， 只达到了0.4465。

 3、随机森林回归

3.1 基本原理

        随机森林回归算法（Random Forest Regression）是随机森林（Random Forest）的重要应用分支。随机森林回归模型通过随机抽取样本和特征，建立多棵相互不关联的决策树，通过并行的方式获得预测结果。每棵决策树都能通过抽取的样本和特征得出一个预测结果，通过综合所有树的结果取平均值，得到整个森林的回归预测结果。

3.2 随机森林回归预测房价

（1）预测y（每平方米价格）

        部分预测结果见表5，模型预测值与真实值的比较见图3，模型的评价指标见表6，特征变量重要性程度见图4。

表5 部分预测结果表

真实值	预测值	真实值	预测值	真实值	预测值
43066	41603	44095	48083	48572	49060
41568	44930	47538	40109	33885	33400
47038	49869	39167	43594	34039	33163
51502	53119	32800	38749	69263	47932
40630	38450	25664	33913	60798	50518
38017	35283	25782	32425	29289	47061
36527	38607	39119	30230	29771	44685
33207	35792	50567	46673	37479	33603
53158	36441	30000	38889	38937	43056
34000	34300	30975	42002	17390	33836
46280	38148	28747	38848	25376	38680
23883	34620	30590	38215	40141	33607
23870	30230	42719	47383	28667	27297

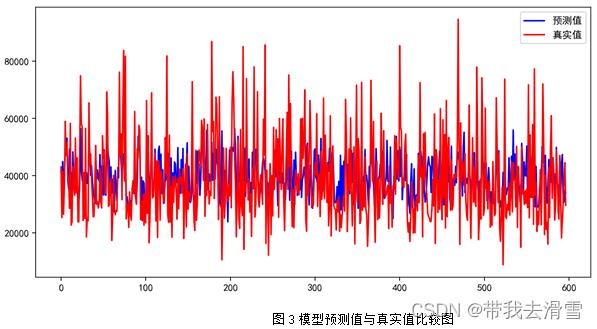
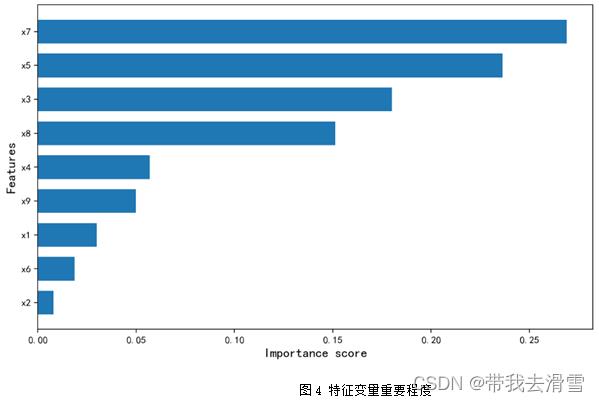
表6模型预测效果评价指标

	RMSE	MAE
0.792	12502.87	9700.34

       通过图4可以看到，使用随机森林回归预测y（每平方米价格），特征变量的重要程度从高到低依次是x7 （房屋附近有无地铁）、x5 （有无电梯）、x3 （房屋面积）、x8 （关注度）、x4 （房屋装修情况）、x9 （看房次数）、x1 （房屋的卧室数量）、x2 （房屋的客厅数量）。通过表6可以发现，使用随机森林回归预测y（每平方米价格），其预测效果较好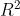， 达到了0.792。

（2）预测 y1 （房屋总价）

       随机森林回归部分预测结果见表7，模型预测值与真实值的比较见图5，模型的评价指标见表8。

表7 部分预测结果表

真实值	预测值	真实值	预测值	真实值	预测值
880	888	195	207	950	846
258	246	480	460	125	157
460	463	600	582	160	204
328	551	320	239	285	386
315	190	380	399	500	1371
200	394	530	465	285	324
152	204	158	176	560	882
370	398	580	409	323	269
305	324	270	263	200	227
350	363	110	154	570	331
420	293	193	168	270	323
357	393	215	296	415	368
398	327	155	196	250	589

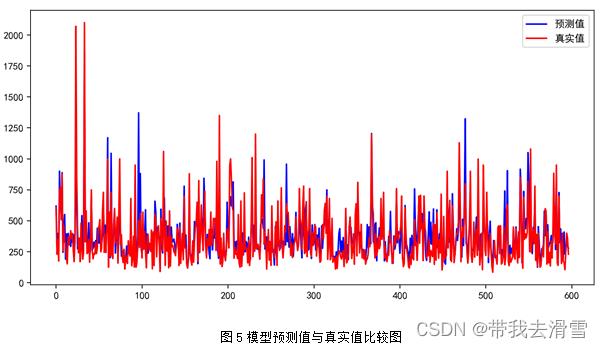
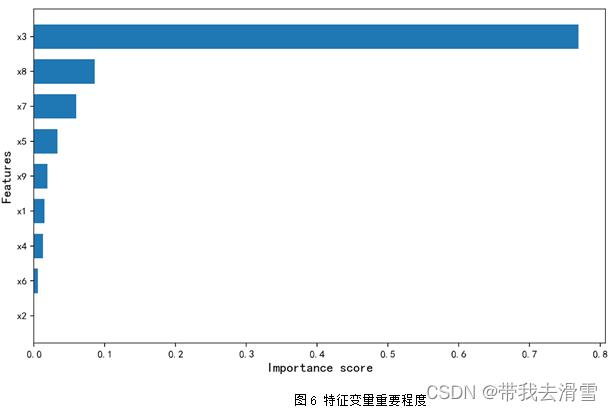
表8模型预测效果评价指标

	RMSE	MAE
0.7596	12502.87	9700.33

        通过图6可以看到，使用随机森林回归预测 y1 （房屋总价），特征变量的重要程度从高到低依次是x3 （房屋面积）、x8 （关注度）、x7 （房屋附近有无地铁）、x5 （有无电梯）、x9 （看房次数）、x1 （房屋的卧室数量）、x4 （房屋装修情况）、x6 （房屋所在楼层位置）、x2 （房屋的客厅数量）。通过表6-8可以发现，使用随机森林回归预测y1 （房屋总价），其预测效果较好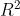，达到了0.7596。

（1）支持向量回归预测房价

import numpy as np

import pandas as pd

import matplotlib.pyplot as plt

import seaborn as sns

from sklearn import preprocessing

from sklearn.preprocessing import StandardScaler

# from sklearn.svm import LinearSVR

from sklearn.svm import SVR

from sklearn.ensemble import RandomForestRegressor

from sklearn.model_selection import train_test_split

from sklearn.metrics import mean_squared_error

from sklearn.metrics import mean_absolute_error

from sklearn.metrics import r2_score

get_ipython().run_line_magic('matplotlib', 'inline')

plt.rcParams['font.sans-serif'] = ['SimHei']

plt.rcParams['axes.unicode_minus'] = False

from IPython.core.interactiveshell import InteractiveShell

InteractiveShell.ast_node_interactivity = 'all'

import warnings

warnings.filterwarnings("ignore")

# # 数据集划分与数据标准化

data = pd.read_excel(r'E:\\工作\\硕士\\学习\\统计软件python\\期末作业\\清洗后数据.xlsx')

data

# X_train, X_valid, y_train, y_valid = train_test_split(X, y, test_size=0.2, random_state = 1234)

# 将数据随机划分成80%训练集和20%测试集

train, test = train_test_split(data, test_size=0.2, random_state = 1234)

train = train.reset_index(drop = True)

test = test.reset_index(drop = True)

train

test

X_train, X_test = train.iloc[:,:-2], test.iloc[:,:-2]

Y_train, Y_test = train.iloc[:,-2], test.iloc[:,-2]

Y1_train, Y1_test = train.iloc[:,-1], test.iloc[:,-1]

# 数据标准化（主要是为了构建支持向量机做准备）

scaler = StandardScaler()

x_scaler = scaler.fit(X_train)

x_train = x_scaler.fit_transform(X_train)

x_test = x_scaler.fit_transform(X_test)

y_scaler = scaler.fit(Y_train.values.reshape(-1,1))

y_train = y_scaler.fit_transform(Y_train.values.reshape(-1,1))

y_test = y_scaler.fit_transform(Y_test.values.reshape(-1,1))

y1_scaler = scaler.fit(Y1_train.values.reshape(-1,1))

y1_train = y1_scaler.fit_transform(Y1_train.values.reshape(-1,1))

y1_test = y1_scaler.fit_transform(Y1_test.values.reshape(-1,1))

# ## 支持向量机

# ### 对y

# #### RBF_SVR

rbf_svr = SVR(kernel = "rbf",  C = 100, epsilon = 0.1)

rbf_svr.fit(x_train, y_train)

# 预测

rbf_svr_pred = rbf_svr.predict(x_test)

y_scaler = scaler.fit(Y_train.values.reshape(-1,1))

y_scaler.fit_transform(Y_train.values.reshape(-1,1))

rbf_svr_pred = y_scaler.inverse_transform(rbf_svr_pred.reshape(-1,1))

# 模型评价

rbf_svr_rmse = np.sqrt(mean_squared_error(Y_test,rbf_svr_pred))    #RMSE

rbf_svr_mae = mean_absolute_error(Y_test,rbf_svr_pred)   #MAE

rbf_svr_r2 = r2_score(Y_test, rbf_svr_pred)  # R2

print("R^2 of RBF_SVR: ", rbf_svr_r2)

print("The RMSE of RBF_SVR: ", rbf_svr_rmse)

print("The MAE of RBF_SVR: ", rbf_svr_mae)

# 输出预测值和真实值矩阵

rbf_svr_pred_true = pd.concat([pd.DataFrame(rbf_svr_pred), pd.DataFrame(Y_test)], axis = 1)

rbf_svr_pred_true.columns = ['预测值', '真实值']

rbf_svr_pred_true.to_excel(r' E:\\工作\\硕士\\学习\\统计软件python\\期末作业\\径向基核支持向量机预测y.xlsx', index = False)

# 比较图

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(rbf_svr_pred, color = 'b', label = '预测值')

plt.plot(Y_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

# #### POLY_SVR

poly_svr = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")

poly_svr.fit(x_train, y_train)

# 预测y

poly_svr_pred = poly_svr.predict(x_test)

y_scaler = scaler.fit(Y_train.values.reshape(-1,1))

y_scaler.fit_transform(Y_train.values.reshape(-1,1))

poly_svr_pred = y_scaler.inverse_transform(poly_svr_pred.reshape(-1,1)) 

# 模型评价

poly_svr_rmse = np.sqrt(mean_squared_error(Y_test,poly_svr_pred))    #RMSE

poly_svr_mae = mean_absolute_error(Y_test,poly_svr_pred)   #MAE

poly_svr_r2 = r2_score(Y_test, poly_svr_pred)  # R2

print("R^2 of POLY_SVR: ", poly_svr_r2)

print("The RMSE of POLY_SVR: ", poly_svr_rmse)

print("The MAE of PLOY_SVR: ", poly_svr_mae)

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(poly_svr_pred, color = 'b', label = '预测值')

plt.plot(Y_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

# ### 对y1

# #### RBF_SVR

rbf1_svr = SVR(kernel = "rbf",  C = 100, epsilon = 0.1)

rbf1_svr.fit(x_train, y1_train)

# 预测y1

rbf1_svr_pred = rbf1_svr.predict(x_test)

y1_scaler = scaler.fit(Y1_train.values.reshape(-1,1))

y1_train = y1_scaler.fit_transform(Y1_train.values.reshape(-1,1))

rbf1_svr_pred = y1_scaler.inverse_transform(rbf1_svr_pred.reshape(-1,1))

# 模型评价

rbf1_svr_rmse = np.sqrt(mean_squared_error(Y1_test,rbf1_svr_pred))    #RMSE

rbf1_svr_mae = mean_absolute_error(Y1_test,rbf1_svr_pred)   #MAE

rbf1_svr_r2 = r2_score(Y1_test, rbf1_svr_pred)  # R2

print("R^2 of RBF_SVR: ", rbf1_svr_r2)

print("The RMSE of RBF_SVR: ", rbf1_svr_rmse)

print("The MAE of RBF_SVR: ", rbf1_svr_mae)

# 输出预测值和真实值矩阵

rbf1_svr_pred_true = pd.concat([pd.DataFrame(rbf1_svr_pred), pd.DataFrame(Y1_test)], axis = 1)

rbf1_svr_pred_true.columns = ['预测值', '真实值']

rbf1_svr_pred_true.to_excel(r' E:\\工作\\硕士\\学习\\统计软件python\\期末作业\\径向基核支持向量机预测y1.xlsx', index = False)

# 画图

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(rbf1_svr_pred, color = 'b', label = '预测值')

plt.plot(Y1_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

# #### POLY_SVR

poly1_svr = SVR(kernel="poly", degree=3, C=100, epsilon=0.1, gamma="scale")

poly1_svr.fit(x_train, y1_train)

# 预测

poly1_svr_pred = poly1_svr.predict(x_test)

y1_scaler = scaler.fit(Y1_train.values.reshape(-1,1))

y1_train = y1_scaler.fit_transform(Y1_train.values.reshape(-1,1))

poly1_svr_pred = y1_scaler.inverse_transform(poly1_svr_pred.reshape(-1,1))

# 模型评价

poly1_svr_rmse = np.sqrt(mean_squared_error(Y1_test,poly1_svr_pred))    #RMSE

poly1_svr_mae = mean_absolute_error(Y1_test,poly1_svr_pred)   #MAE

poly1_svr_r2 = r2_score(Y1_test, poly1_svr_pred)  # R2

print("R^2 of POLY_SVR: ", poly1_svr_r2)

print("The RMSE of POLY_SVR: ", poly1_svr_rmse)

print("The MAE of POLY_SVR: ", poly1_svr_mae)

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(poly1_svr_pred, color = 'b', label = '预测值')

plt.plot(Y1_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

（2）随机森林回归预测房价

## 模型建立与预测

### 随机森林

#### 对y

rf = RandomForestRegressor(n_estimators = 1000, max_depth = 6, random_state = 1234)

rf.fit(X_train, Y_train)

rf_pred = rf.predict(X_test)

# 模型评价

rf_rmse = np.sqrt(mean_squared_error(Y_test,rf_pred))    #RMSE

rf_mae = mean_absolute_error(Y_test,rf_pred)   #MAE

rf_r2 = r2_score(Y_test, rf_pred)  # R2

print("R^2 of RandomForest: ", rf_r2)

print("The RMSE of RandomForest: ", rf_rmse)

print("The MAE of RandomForest: ", rf_mae)

# 输出预测值和真实值矩阵

rf_pred_true = pd.concat([pd.DataFrame(rf_pred), pd.DataFrame(Y_test)], axis = 1)

rf_pred_true.columns = ['预测值', '真实值']

rf_pred_true.to_excel(r'E:\\工作\\硕士\\学习\\统计软件python\\期末作业\\ \\随机森林预测y.xlsx ', index = False)

# 比较图

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(rf_pred, color = 'b', label = '预测值')

plt.plot(Y_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

dic = dict(zip(X_train.columns, rf.feature_importances_))

dic = dict(sorted(dic.items(),key=lambda x:x[1]))

rf_fea_name = [key for key,value in dic.items() ]

rf_fea = [value for key,value in dic.items() ]

plt.figure(figsize = (10,6), dpi = 200)

plt.barh(rf_fea_name, rf_fea, height = 0.7)

plt.xlabel('Importance score', fontsize = 13)

plt.ylabel('Features', fontsize = 13)

# ### 对y1

rf1 = RandomForestRegressor(n_estimators = 1000, max_depth = 6, random_state = 1234)

rf1.fit(X_train, Y1_train)

rf1_pred = rf1.predict(X_test)

# 模型评价

rf1_rmse = np.sqrt(mean_squared_error(Y1_test,rf1_pred))    #RMSE

rf1_mae = mean_absolute_error(Y1_test,rf1_pred)   #MAE

rf1_r2 = r2_score(Y1_test, rf1_pred)  # R2

print("R^2 of RandomForest: ", rf1_r2)

print("The RMSE of RandomForest: ", rf1_rmse)

print("The MAE of RandomForest: ", rf1_mae)

# 输出预测值和真实值矩阵

rf1_pred_true = pd.concat([pd.DataFrame(rf1_pred), pd.DataFrame(Y1_test)], axis = 1)

rf1_pred_true.columns = ['预测值', '真实值']

rf1_pred_true.to_excel(r' E:\\工作\\硕士\\学习\\统计软件python\\期末作业\\随机森林预测y1', index = False)

# 比较图

plt.subplots(figsize=(10,5), dpi = 200)

plt.plot(rf1_pred, color = 'b', label = '预测值')

plt.plot(Y1_test, color = 'r', label = '真实值')

plt.legend(loc = 0)

dic = dict(zip(X_train.columns, rf1.feature_importances_))

dic = dict(sorted(dic.items(),key=lambda x:x[1]))

rf_fea_name = [key for key,value in dic.items() ]

rf_fea = [value for key,value in dic.items() ]

plt.figure(figsize = (10,6), dpi = 200)

plt.barh(rf_fea_name, rf_fea, height = 0.7)

plt.xlabel('Importance score', fontsize = 13)

plt.ylabel('Features', fontsize = 13)

需要数据集的家人们可以去百度网盘（永久有效）获取：

链接：https://pan.baidu.com/s/16GeXC9_f6KI4lS2wQ-Z1VQ?pwd=2138
提取码：2138 

---

更多优质内容持续发布中，请移步主页

   点赞+关注,下次不迷路！