机器学习中的贝叶斯方法---先验概率似然函数后验概率的理解及如何使用贝叶斯进行模型预测

Posted 2020-09-07 hapjin

一，本文将基于“独立重复试验---抛硬币”来解释贝叶斯理论中的先验概率、似然函数和后验概率的一些基础知识以及它们之间的关系。

本文是《A First Course of Machine Learning》的第三章的学习笔记，在使用贝叶斯方法构造模型并用它进行预测时，总体思路是：在已知的先验知识(先验概率分布)的条件下，根据实际观察到的数据(现有的训练样本)尽可能最大化似然函数，然后，使用边界似然函数(marginal likelihood)选择最合适的模型参数，将该模型参数代入后验概率分布中，使用后验概率分布的期望进行未知样本的预测。简洁地讲就是：

• ①先验知识 就是 我们预先对模型参数的一些了解
• ②在给定的样本数据下，找一个概率分布函数或者概率密度函数(似然函数)，使得这些已发生的事件(得到的样本数据)，出现的概率是最大的(参考：使用最大似然法来求解线性模型（2）-为什么是最大化似然函数？）。
• ③基于先验概率分布 和 似然函数 计算后验概率分布，再使用后验概率分布 来预测未知数据。

其实②很好理解，假设现在已经观测到了一批样本数据，我为这批数据选择了三个概率密度函数(概率分布函数)，p₁(data)，p₂(data)，p₃(data)

p₁(data)认为这批数据出现的概率是0.6，p₂(data)认为这批数据出现的概率是0.8，p₃(data)认为这批数据出现的概率是0.95

由于我们得到了这批样本数据，表示：这批数据所代表的事件已经实际发生了，显然p₃(data)是最合适的概率分布函数(密度函数)，那么使用p₃(data)中的参数来计算后验概率分布，并由此得到的预测模型是最”准确“的。

 

二，抛硬币示例

首先为抛硬币制定一个规则。押一块钱，抛10次硬币，出现正面的次数小于等于6次就额外赢得一块钱，否则就是输掉押的一块钱。定义随机变量X和Y如下：

随机变量Y表示，出现正面的次数，随机变量X表示抛10次硬币输赢的结果，当Y<=6时，X=1，表示赢了；当Y>6时，X=0表示输了。

 

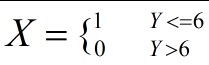
当赢了之后，一块钱就变成了2块钱。输了之后，一块钱就变成了0，定义函数f(X)表示赌博之后的结果：

 

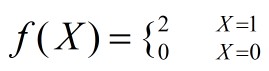
正常情况下，根据常识：

1. 抛硬币出现正面的概率等于出现反面的概率等于0.5，即p(正面)=p(反面)=0.5
2. 第一次抛硬币的结果 不会影响 第二次抛硬币的结果。假如我抛了10次硬币，即做了10次实验，这10次实验的结果是相互独立的
3. 我可以不断地重复地抛硬币，因此它是一个可重复的试验，结合上面第2点，也就是一个独立可重复试验。

根据概率论知识：上述抛硬币实验服从二项分布B(N,p)，N是进行的实验的次数，p是发生某种结果的概率，在这里p就是出现正面的概率，p=0.5

对于二项分布，所谓二项，即：做一次实验后，它只会出现二种结果，比如上面的抛硬币，要么 出现正面，要么出现反面，没有其他第三种结果。二项分布常用来对独立可重复实验进行概率建模。它的概率分布函数如下：一共抛了N次硬币，Y表示出现硬币正面的次数，r 表示抛一次硬币 出现 正面的概率

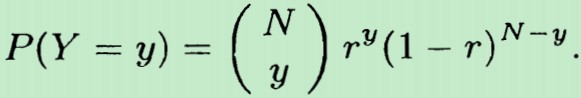
根据我们的假设，N=10,P=0.5。得到P(y<=6)=0.8281. 这意味着我们有0.8218的概率赢钱。赢到的钱数期望是：E{f(x)}=2*0.8281+0*(1-0.8281)=1.6562

也就是说，在抛硬币出现正面和反面概率相同(都是0.5)的情况下，根据游戏规则，抛10次硬币进行一次游戏，押1块钱，最终能得到1.6562块钱。基于这个信息，这个游戏是值得玩的。

 

经过上面的抛硬币示例分析，哪些信息是先验信息呢？---最重要的先验信息就是：抛一次硬币，出现正面和反面的概率是一样的，都是0.5

如果我们把 r 也视为一个随机变量，那么N次独立重复的抛硬币实验的概率分布函数，可写成如下的条件概率的形式：

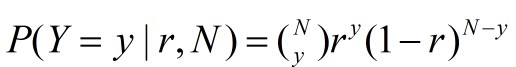
现在，换种思路，万一有人对硬币做了手脚，使得抛一次硬币，出现正面的概率 与 出现反面的概率 不一样呢？

现在，在 r 未知的情况下(有人对硬币做了手脚了)， 我们拿到了一组数据(样本信息)，有个人抛了10次硬币，其中出现了9次正面，一次反面。我们有多少理由相信，r=0.5？即抛一次硬币出现正面的概率和出现反面的概率还是相等的？

根据二项概率分布，可表示为：

我们的目标是：在现有的观测结果下---抛了10次硬币，其中出现了9次正面，一次反面：

让P(Y=y|r,N)取最大值。那么 r 究竟等于多少，才能使得P(Y=y|r,N)最大呢？也即 r 究竟取多少，才能使得抛了10次硬币，其中出现了9次正面，一次反面 发生的概率是最大的？这也是最大化似然函数的原理。

 

为了更方便地计算最大值，对上面的概率分布取对数log，用L表示，得到下式：

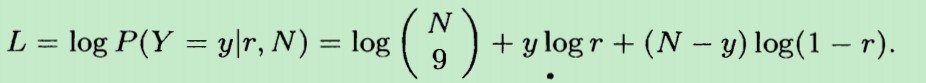
L称为似然函数。最大化P(Y=y|r,N) 与 最大化 LogP(Y=y|r,N) 等价，因为log函数是单调递增函数，不影响最大化结果，取对数是为了计算上的方便。

将 L 对 r 求偏导数，并且令偏导数等于0，其中N=10，y=9。解得 r = 0.9

 

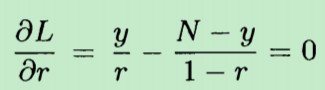
换句话说，抛了10次硬币，9次正面向上，1次向下。我们有理由相信：抛硬币出现正面的概率 和 出现反面的概率是不相等的。从观测的样本数据结果来看，通过最大化似然函数，我们认为：抛一次硬币出现正面的概率是0.9，出现反面的概率是0.1。也即 r = 0.9

在 r = 0.9 的条件下，

因此，在这种情况下，我们押1块钱，最终的结果是只剩下0.0256块钱了：

E(f(X))=

 

根据上面的计算结果可知：由于观察到10次抛硬币结果，有9次出现了正面。如果按照规则：抛10次硬币，出现正面的次数小于等于6次，才算我们赢，那这游戏不能玩了。

 

三，总结

在上面我们解释了两个重要的概念：一个是先验信息，另一个是似然函数。所谓先验信息，就是在进行一次试验之前，我们所掌握的一些信息。比如抛硬币试验，我们掌握的先验信息是：

• 硬币出现正面的概率和出现反面的概率相等，都为0.5

又或者是：

• 出现正面的概率和出现反面的概率不相等，出现正面的概率要大于出现反面的概率

 

而似然函数则是指，我们现在拥有了一些样本数据，或者说是进行了一些实验，观测到了一些数据。在观测到的这些数据之后，如果基于这些观测到的数据，为这些数据寻找一个合适的模型，确定出该模型中的各个参数的值。比如上面的10次抛硬币试验，9次正面，1次反面，我们采用的模型是二项分布，模型中的参数 r 等于0.9 最为合适。

 

下一篇文章，将在先验信息 和 似然函数 的基础上，求解 后验概率分布，并使用后验概率分布函数的期望 对 未知的数据 进行预测。而这就是贝叶斯推断的基本原理。

 

相关文章：

使用最大似然法来求解线性模型（1）

使用最大似然法来求解线性模型（2）-为什么是最大化似然函数？

使用最大似然法来求解线性模型（3）-求解似然函数

使用最大似然法来求解线性模型（4）-最大化似然函数背后的数学原理

 

原文：http://www.cnblogs.com/hapjin/p/6653920.html

参考：《A FIrst Course of machine learning》