大话数据结构之查找

Posted 2021-07-25 -恰饭第一名-

一、二叉排序树

（又称为二叉查找树）它或者是一颗空树，或者是具有下列性质的二叉树

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结构的值；
• 若它的右子树不空，则右子树所有的结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树

构造一颗二叉排序树的目的，其实并不是为了排序，而是为了提高查找和插入删除关键字的速度

1、二叉排序树查找操作

/* 二叉树的二叉链表结点结构定义 */
typedef  struct BiTNode	/* 结点结构 */
{
	int data;	/* 结点数据 */
	struct BiTNode *lchild, *rchild;	/* 左右孩子指针 */
} BiTNode, *BiTree;

/* 递归查找二叉排序树T中是否存在key, */
/* 指针f指向T的双亲，其初始调用值为NULL */
/* 若查找成功，则指针p指向该数据元素结点，并返回TRUE */
/* 否则指针p指向查找路径上访问的最后一个结点并返回FALSE */
Status SearchBST(BiTree T, int key, BiTree f, BiTree *p) 
{  
	/*下面的if循环用来判断当前二叉树是否到叶子结点*/
	if (!T)	/*  查找不成功 */
	{ 
		*p = f;  
		return FALSE; 
	}
	else if (key==T->data) /*  查找成功 */
	{ 
		*p = T;  
		return TRUE; 
	} 
	else if (key<T->data) 
		return SearchBST(T->lchild, key, T, p);  /*  在左子树中继续查找 */
	else  
		return SearchBST(T->rchild, key, T, p);  /*  在右子树中继续查找 */
}

---

2、二叉排序树插入操作

/*  当二叉排序树T中不存在关键字等于key的数据元素时， */
/*  插入key并返回TRUE，否则返回FALSE */
Status InsertBST(BiTree *T, int key) 
{  
	BiTree p,s;
	if (!SearchBST(*T, key, NULL, &p)) /* 查找不成功 */
	{
		s = (BiTree)malloc(sizeof(BiTNode));
		s->data = key;  
		s->lchild = s->rchild = NULL;  
		if (!p) 
			*T = s;			/*  插入s为新的根结点 */
		else if (key<p->data) 
			p->lchild = s;	/*  插入s为左孩子 */
		else 
			p->rchild = s;  /*  插入s为右孩子 */
		return TRUE;
	} 
	else 
		return FALSE;  /*  树中已有关键字相同的结点，不再插入 */
}

3、二叉排序树删除操作

根据我们对删除结点的三种情况的分析：

• 叶子结点
• 仅有左或右子树的结点
• 左右子树都有的结点，下面这个算法是递归方式对二叉排序树T查找key，查找到时删除

/* 若二叉排序树T中存在关键字等于key的数据元素时，则删除该数据元素结点, */
/* 并返回TRUE；否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key)
{ 
	if(!*T) /* 不存在关键字等于key的数据元素 */ 
		return FALSE;
	else
	{
		if (key==(*T)->data) /* 找到关键字等于key的数据元素 */ 
			return Delete(T);
		else if (key<(*T)->data)
			return DeleteBST(&(*T)->lchild,key);
		else
			return DeleteBST(&(*T)->rchild,key);
		 
	}
}

这段代码和前面的二叉排序树查找几乎完全相同，唯一的区别就在于第8行，此时执行的是Delete方法，对当前结点进行删除操作

/* 从二叉排序树中删除结点p，并重接它的左或右子树。 */
Status Delete(BiTree *p)
{
	BiTree q,s;
	if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树（待删结点是叶子也走此分支) */
	{
		q=*p; *p=(*p)->lchild; free(q);
	}
	else if((*p)->lchild==NULL) /* 只需重接它的右子树 */
	{
		q=*p; *p=(*p)->rchild; free(q);
	}
	else /* 左右子树均不空 */
	{
		q=*p; s=(*p)->lchild;
		/*将要删除的结点p赋值给临时的变量q，
		再将q的左孩子p->lchild赋值给临时的变量s。
		此时q指向47结点，s指向35结点*/

		/*循环找到左子树的右结点，直到右侧尽头。
		就当前例子来说就是让q指向35，
		而s指向了37这个再没有右子树的结点*/
		while(s->rchild) /* 转左，然后向右到尽头（找待删结点的前驱） */
		{
			q=s;
			s=s->rchild;
		}
		
		/*此时让要删除的结点P的位置的数据被赋值为s->data,
		即让p->data=37*/
		(*p)->data=s->data; /*  s指向被删结点的直接前驱（将被删结点前驱的值取代被删结点的值） */

		/*如果p和q指向不同，则将s->lchild赋值给q->rchild,否则，否则是将s->lchild赋值给q->lchild。显然这个例子p不等于q,将s->lchild指向的36赋值给q->rchild，也就是让q->rchild指向36结点*/
		if(q!=*p)
			q->rchild=s->lchild; /*  重接q的右子树 */ 
		else
			q->lchild=s->lchild; /*  重接q的左子树 */
		free(s);
	}
	return TRUE;
}

4、二叉排序树总结

二叉排序树是以链接的方式存储，保持了链接存储结构再执行插入或删除操作时不用移动元素的优点，只要找到合适的插入和删除位置后，仅需修改链接指针即可


对于二叉排序树的查找，走的就是从根结点到要查找的结点的路径，其比较次数等于给定值的结点再二叉排序树的层次

---

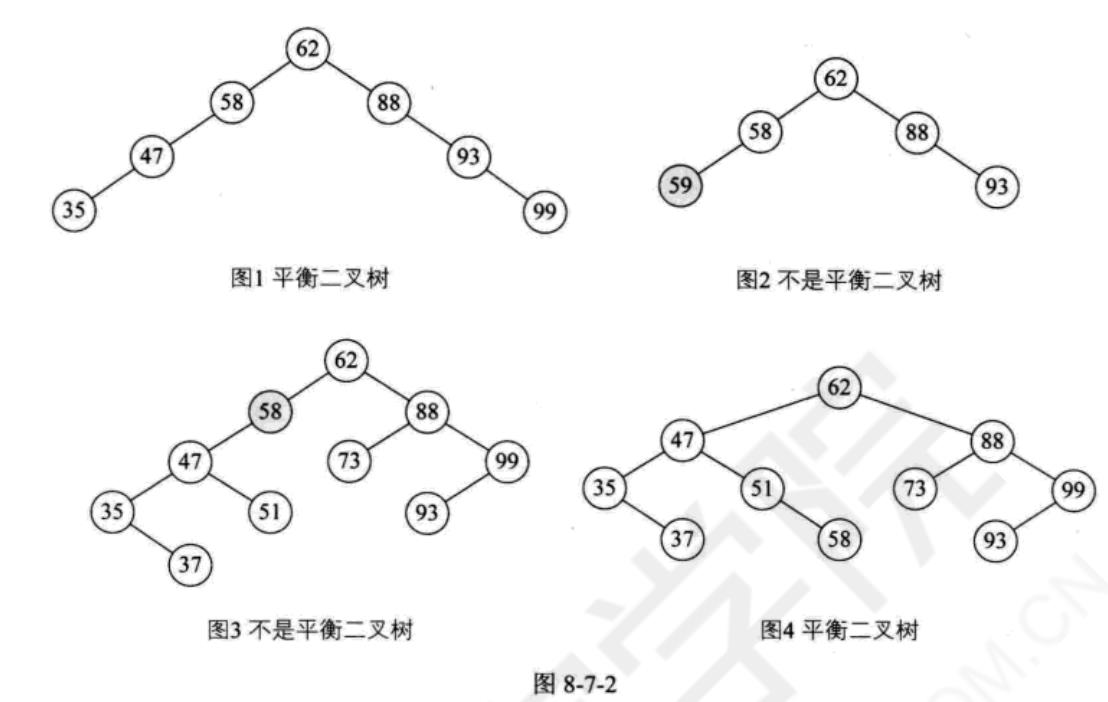
二、平衡二叉树（AVL树）

平衡二叉树是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1

平衡因子BF

二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF

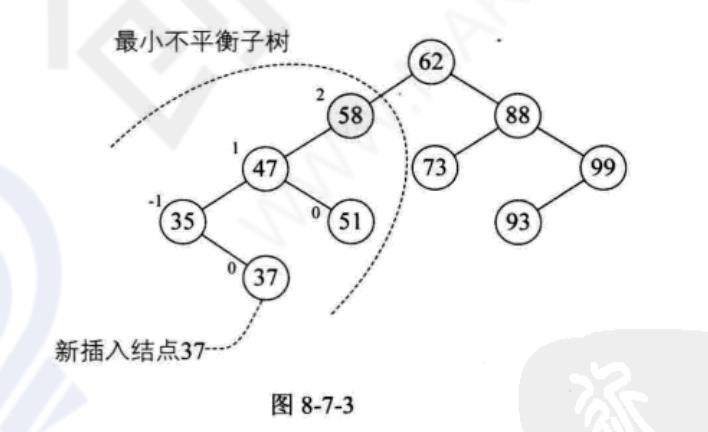
最小不平衡子树

距离插入结点最近的，且平衡因子的绝对值大于1的结点为根的子树
当新插入结点37时，距离它最近的平衡因子绝对值超过1的结点是58（即它的左子树高度2减去右子树高度0），所以从58开始以下的子树为最小不平衡子树

1、平衡二叉树实现原理

平衡二叉树构建的基本思想就是在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树
在保持二叉排序树特性的前提下，调整最小不平衡子树中各节点之间的链接关系，进行相应的旋转，使之成为新的平衡子树

---

我们先讲一个平衡二叉树构建过程的例子，假设我们现在有一个数组a[10]={3,2,1,4,5,6,7,10,9,8}需要构建二叉排序树

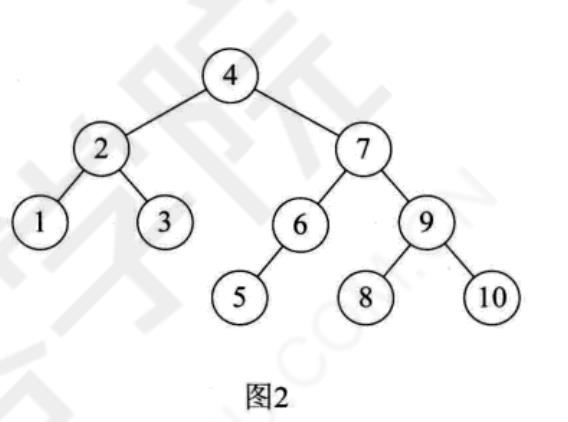
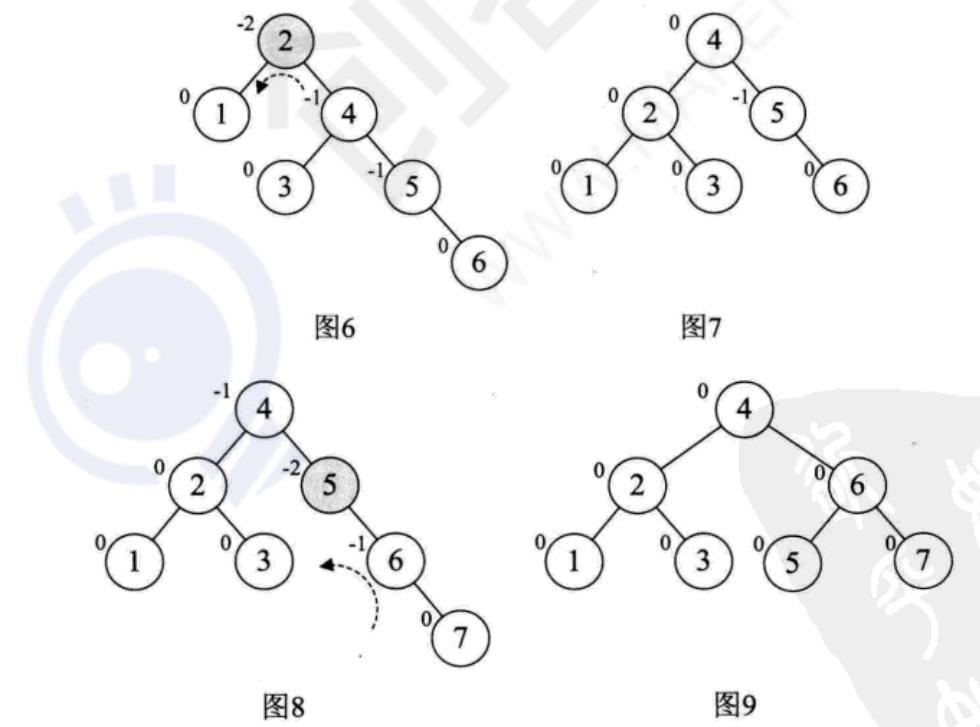
对于数组a[10]={3，2，1，4，5，6，7，10，9，8}的前两位3和2，我们很正常地构建，到了第3个数“1”时，发现此时根结点“3”的平衡因子变成了2，此时整棵树都成了最小平衡子树，因此需要调整，如图1（结点左上角数字为平衡因子BF值）。因为BF值为正，因此我们将整个树进行右旋（顺时针旋转），此时结点2成了根结点，3成了2的右孩子，这样三个结点的BF值均为0，如图2

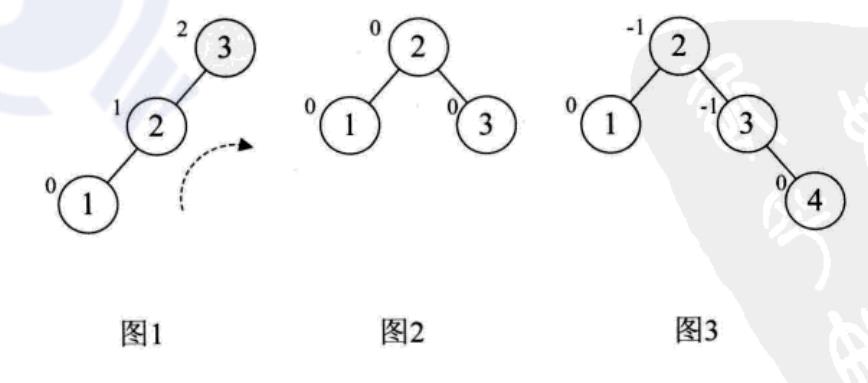
然后我们再增加结点4，平衡因子没发生改变，如图3。增加结点5时，结点3的BF值为-2，说明要旋转了。由于BF是负值，所以我们对这颗最小平衡子树进行左旋（逆时针旋转），如图4

增加结点6时，发现根结点2的BF值变成了-2，如图6.所以我们对根结点进行左旋，注意此时本来结点3是4的左孩子，由于旋转后需要满足二叉排序树特性，因此它成了结点2的右孩子，如图7。增加结点7，同样的左旋转，使得整棵树达到平衡

当增加结点10时，结构无变化，如图10.再增加结点9，此时结点7的BF变成了-2，理论上我们只需要旋转最小不平衡子树7、9、10即可，但是如果左旋转后，结点9就成了10的右孩子，这是不符合二叉排序树的特性的，此时不能简单的左旋，如图11所示

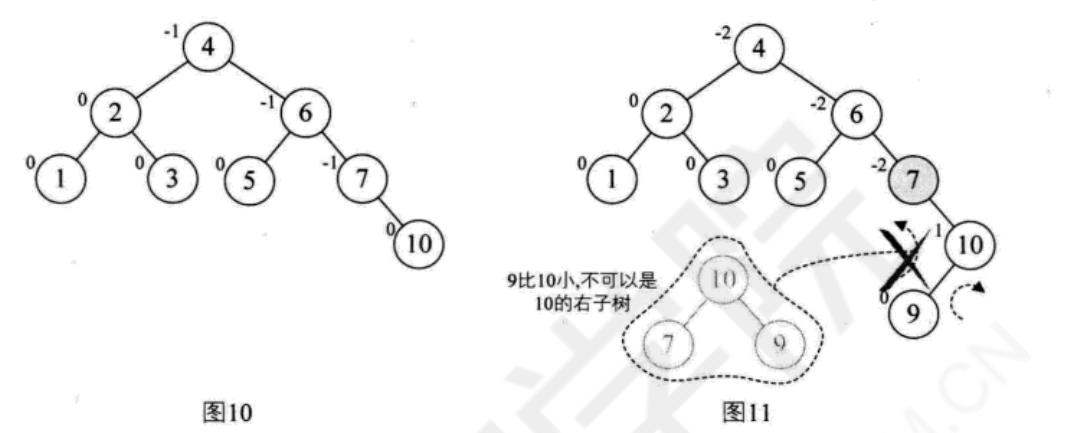
仔细观察图11，发现根本愿意在于结点7的BF是-2，而结点10的BF是1，也就是说，它们俩一正一负，符合并不统一，而前面的几次旋转，无论左还是右旋，最小不平衡子树的根结点与它的子节点符合都是相同的。这就是不能直接旋转的关键。那怎么办呢？

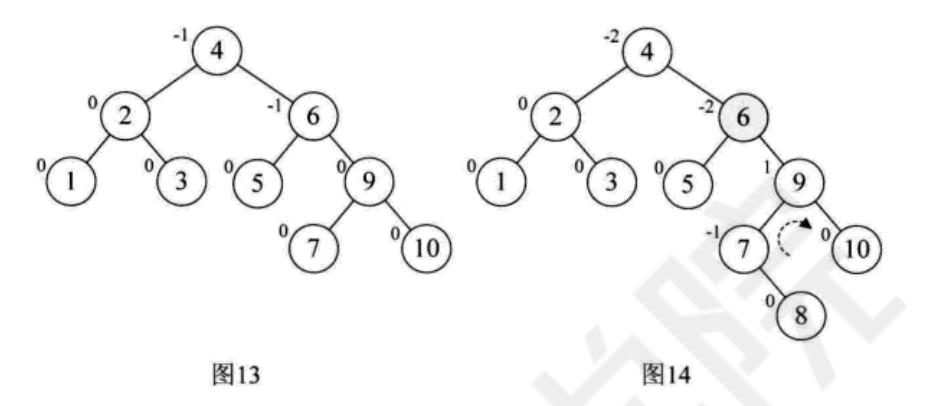
于是我们先对结点9和结点10进行右旋，使得结点10成了9的右子树，结点9的BF为-1，此时就与结点7的BF值符号统一了，如图12

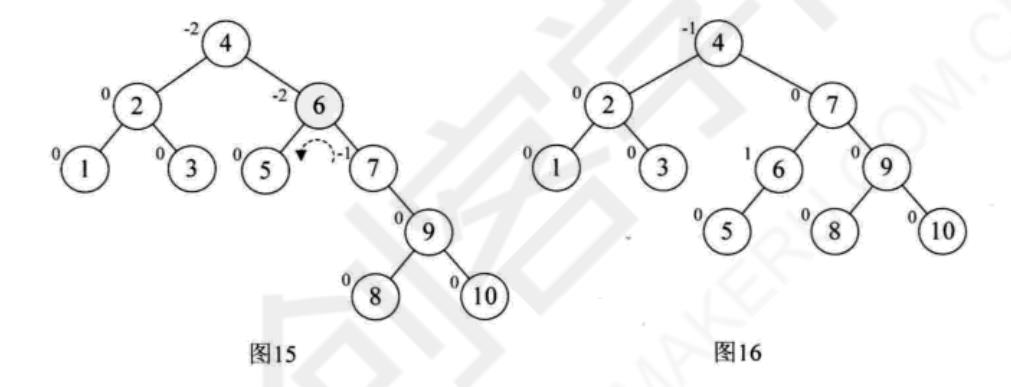
这样我们再以结点7为最小不平衡子树进行左旋，得到图13，接着插入8，情况与刚才类似，结点6的BF是-2，而它的右孩子9的BF是1，如图14，因此首先以9为根结点，进行右旋，得到图15，此时结点6和结点7的符合都是负，再以6为根结点左旋，最终得到最后的平衡二叉树，如图16

2、平衡二叉树实现算法

改进二叉树排序树的结点结构，增加一个bf，用来存储平衡因子

/* 二叉树的二叉链表结点结构定义 */
typedef  struct BiTNode	/* 结点结构 */
{
	int data;	/* 结点数据 */
	int bf; /*  结点的平衡因子 */ 
	struct BiTNode *lchild, *rchild;	/* 左右孩子指针 */
} BiTNode, *BiTree;

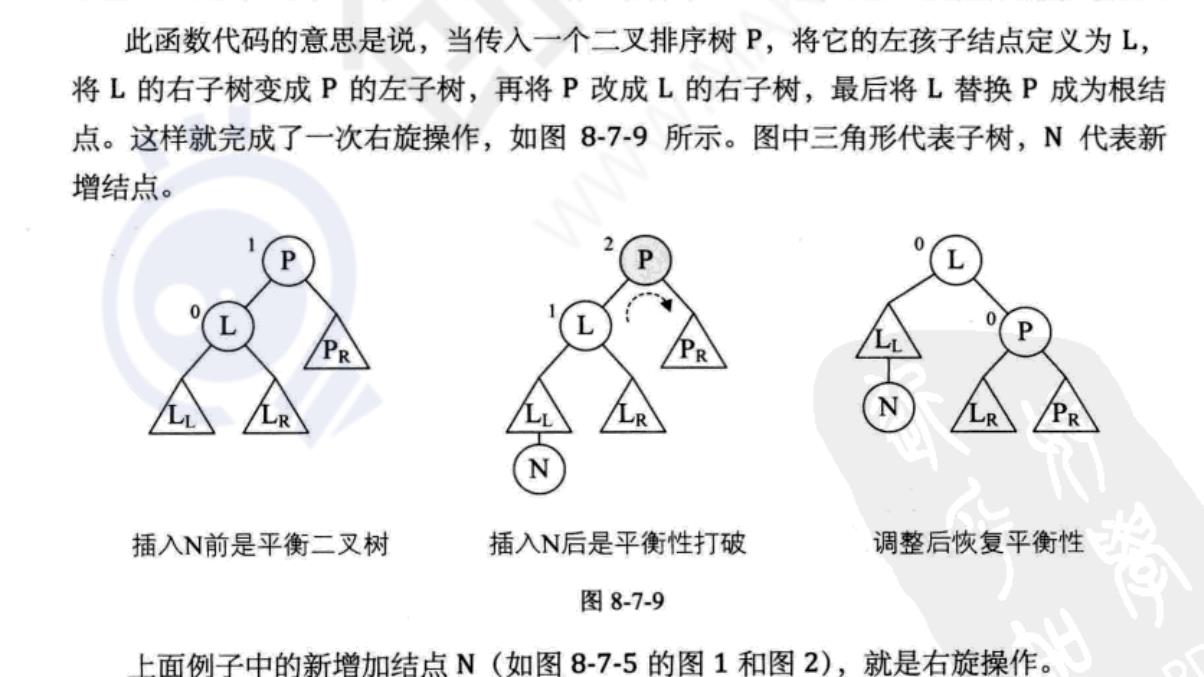
（1）右旋操作

/* 对以p为根的二叉排序树作右旋处理， */
/* 处理之后p指向新的树根结点，即旋转处理之前的左子树的根结点 */
void R_Rotate(BiTree *P)
{ 
	BiTree L;
	L=(*P)->lchild; /*  L指向P的左子树根结点 */ 
	(*P)->lchild=L->rchild; /*  L的右子树挂接为P的左子树 */ 
	L->rchild=(*P);
	*P=L; /*  P指向新的根结点 */ 
}

（2）左旋操作

/* 对以P为根的二叉排序树作左旋处理， */
/* 处理之后P指向新的树根结点，即旋转处理之前的右子树的根结点0  */
void L_Rotate(BiTree *P)
{ 
	BiTree R;
	R=(*P)->rchild; /*  R指向P的右子树根结点 */ 
	(*P)->rchild=R->lchild; /* R的左子树挂接为P的右子树 */ 
	R->lchild=(*P);
	*P=R; /*  P指向新的根结点 */ 
}

左平衡旋转处理的函数代码：

#define LH +1 /*  左高 */ 
#define EH 0  /*  等高 */ 
#define RH -1 /*  右高 */ 

/*  对以指针T所指结点为根的二叉树作左平衡旋转处理 */
/*  本算法结束时，指针T指向新的根结点 */
void LeftBalance(BiTree *T)
{ 
	BiTree L,Lr;
	L=(*T)->lchild; /*  L指向T的左子树根结点 */ 
	switch(L->bf)
	{ /*  检查T的左子树的平衡度，并作相应平衡处理 */ 
		 case LH: /*  新结点插入在T的左孩子的左子树上，要作单右旋处理 */ 
			(*T)->bf=L->bf=EH;
			R_Rotate(T);
			break;
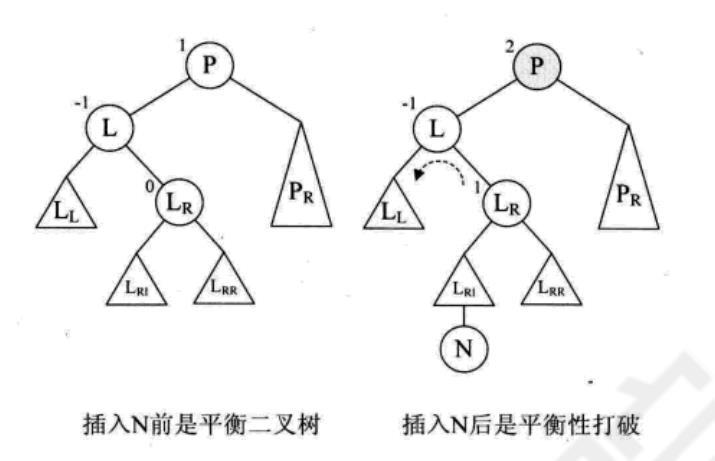
		 case RH: /*  新结点插入在T的左孩子的右子树上，要作双旋处理 */ 
			Lr=L->rchild; /*  Lr指向T的左孩子的右子树根 */ 
			switch(Lr->bf)
			{ /*  修改T及其左孩子的平衡因子 */ 
				case LH: (*T)->bf=RH;
						 L->bf=EH;
						 break;
				case EH: (*T)->bf=L->bf=EH;
						 break;
				case RH: (*T)->bf=EH;
						 L->bf=LH;
						 break;
			}
			Lr->bf=EH;
			L_Rotate(&(*T)->lchild); /*  对T的左子树作左旋平衡处理 */ 
			R_Rotate(T); /*  对T作右旋平衡处理 */ 
	}
}

右平衡旋转处理的函数代码：

/*  对以指针T所指结点为根的二叉树作右平衡旋转处理， */ 
/*  本算法结束时，指针T指向新的根结点 */ 
void RightBalance(BiTree *T)
{ 
	BiTree R,Rl;
	R=(*T)->rchild; /*  R指向T的右子树根结点 */ 
	switch(R->bf)
	{ /*  检查T的右子树的平衡度，并作相应平衡处理 */ 
	 case RH: /*  新结点插入在T的右孩子的右子树上，要作单左旋处理 */ 
			  (*T)->bf=R->bf=EH;
			  L_Rotate(T);
			  break;
	 case LH: /*  新结点插入在T的右孩子的左子树上，要作双旋处理 */ 
			  Rl=R->lchild; 			/*  Rl指向T的右孩子的左子树根 */ 
			  switch(Rl->bf)
			  { 						/*  修改T及其右孩子的平衡因子 */ 
				case RH: (*T)->bf=LH;
						 R->bf=EH;
						 break;
				case EH: (*T)->bf=R->bf=EH;
						 break;
				case LH: (*T)->bf=EH;
						 R->bf=RH;
						 break;
			  }
			  Rl->bf=EH;
			  R_Rotate(&(*T)->rchild); /*  对T的右子树作右旋平衡处理 */ 
			  L_Rotate(T); /*  对T作左旋平衡处理 */ 
	}
}

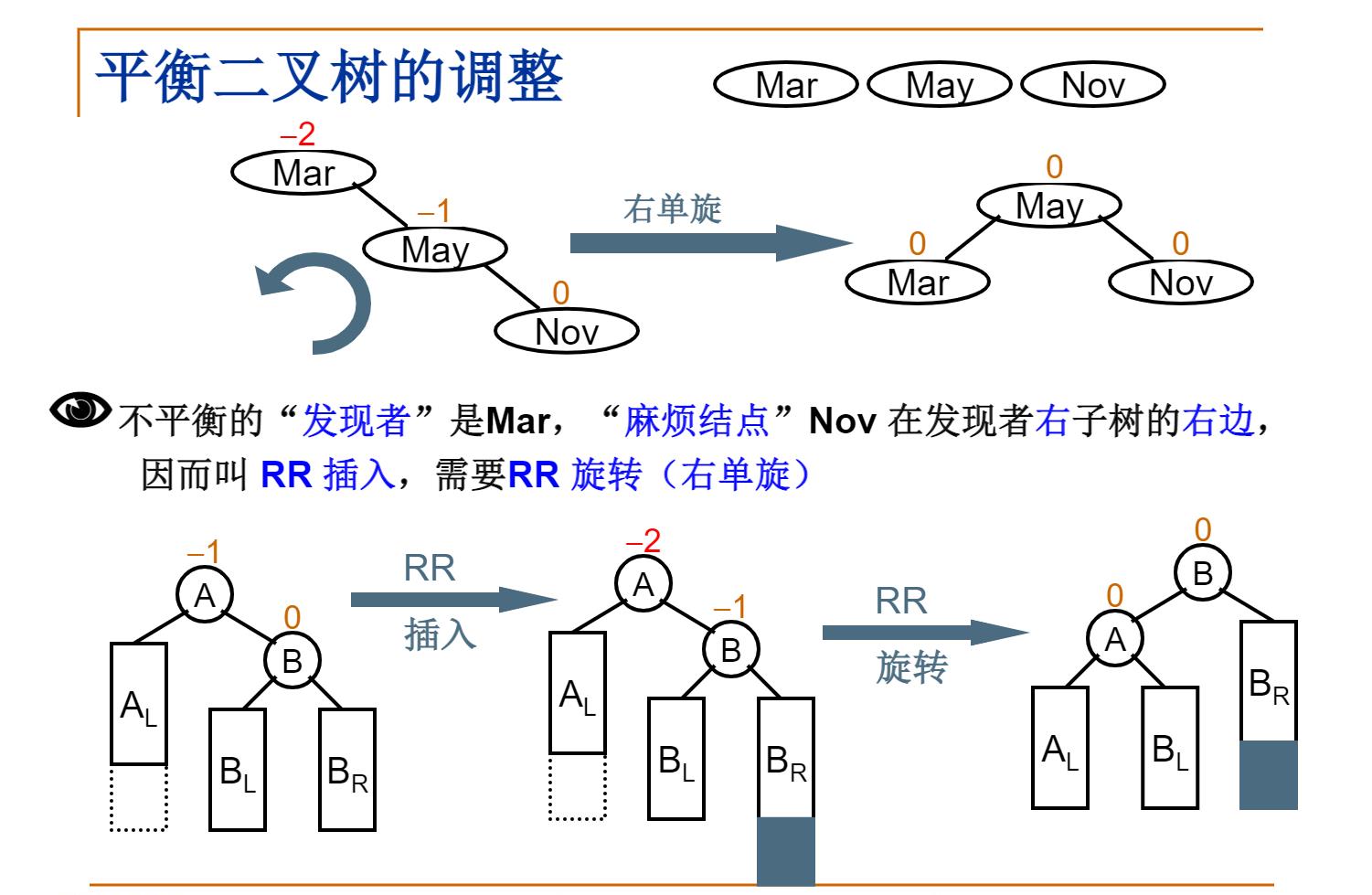
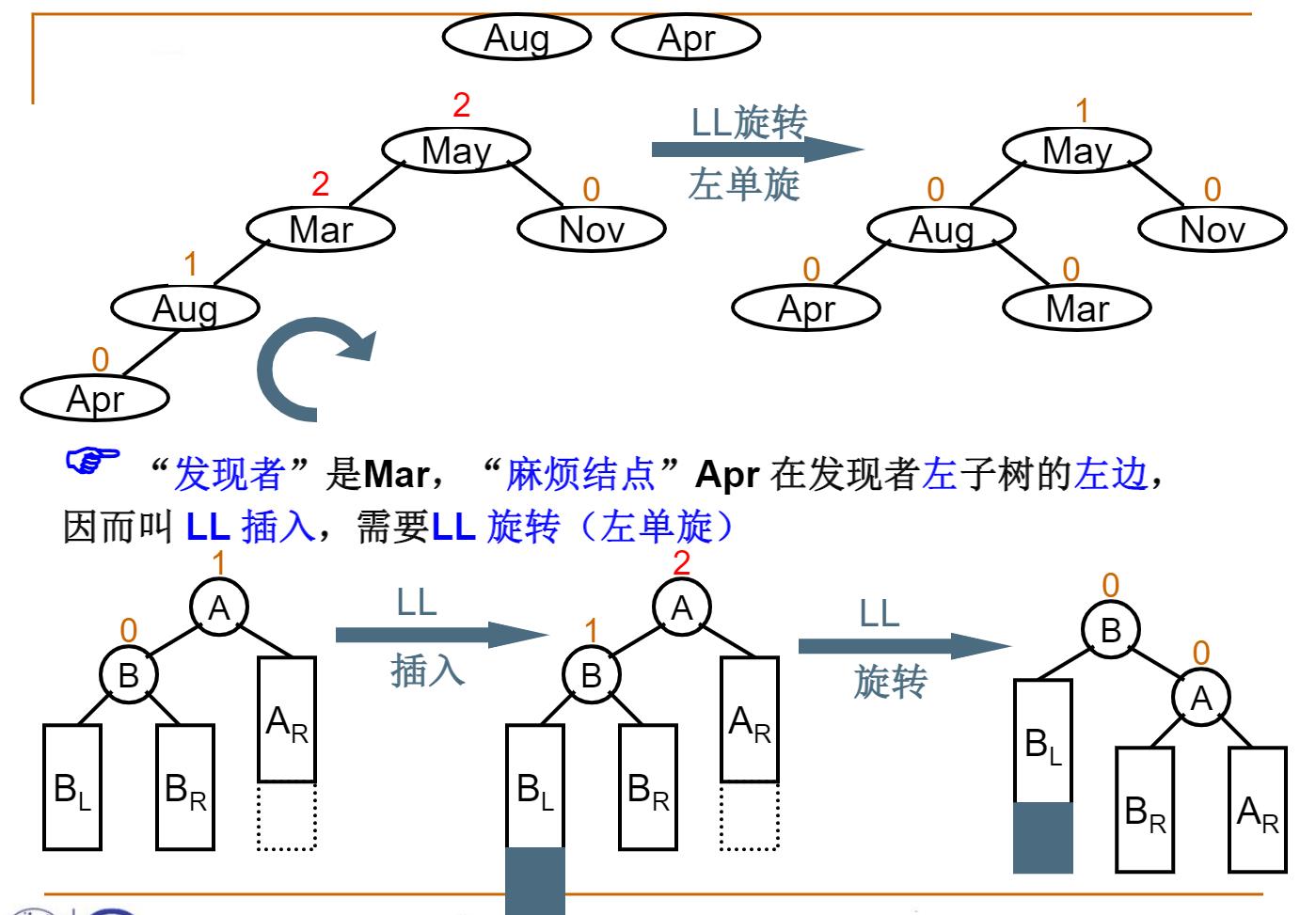
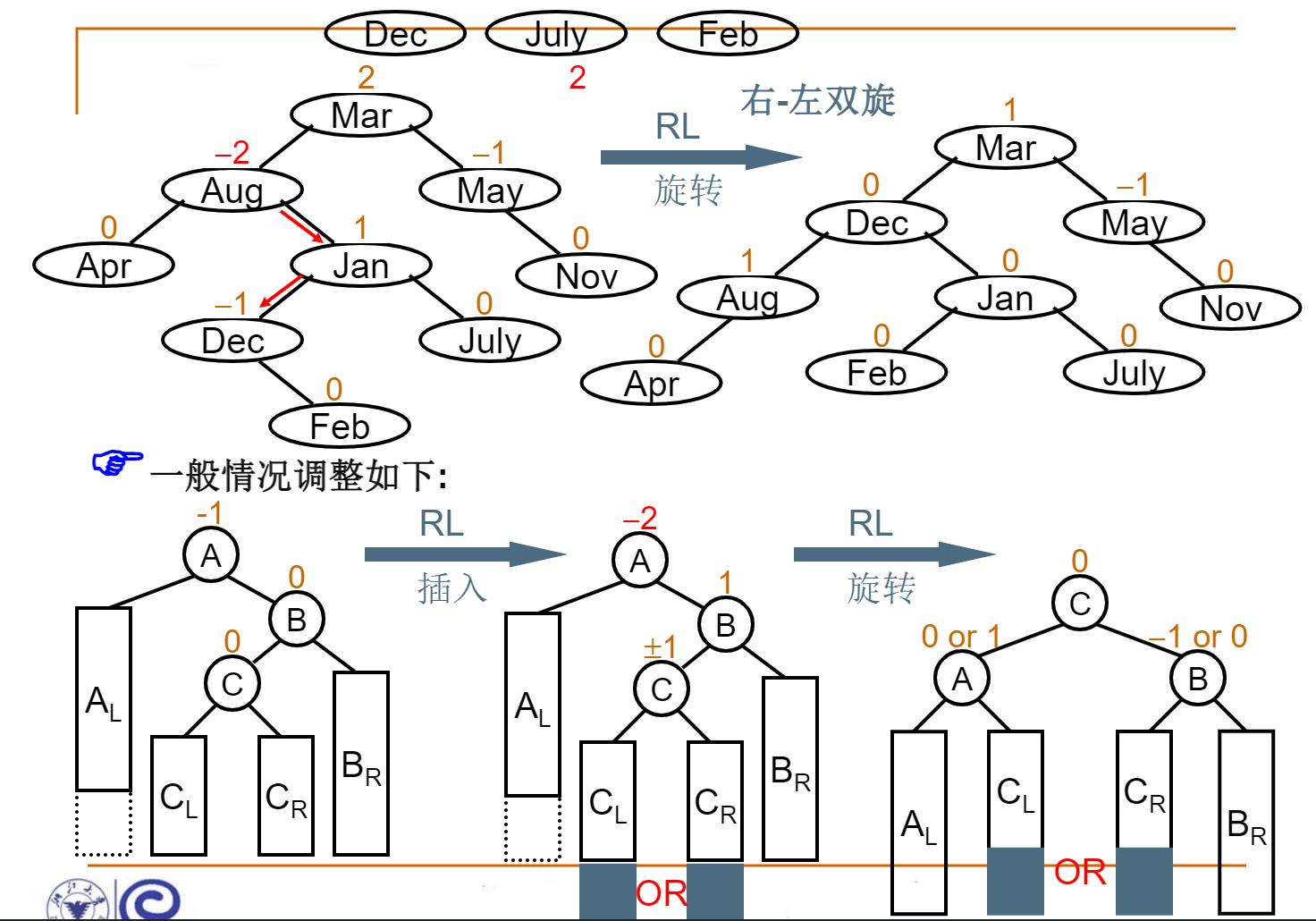
三、平衡二叉树的调整