双足轮机器人Ascento技术详解--建模控制翻译

Posted 2021-07-16 灯哥开源

Ⅲ 建模

为了使用基于模型的控制策略以及现代状态估计技术，需要一个描述机器人刚体动力学的系统模型。

A. 坐标和符号规定

1. 旋转规定：$\dot{a}$ 表示对时间的导数， ̂$\hat{a}$表示一个状态，$A^T$是一个矩阵的转置，$a_l$ 和 $a_r$ 分别是左侧和右侧的对称量。
2. 广义坐标和规定：为了建立出在 Ⅲ-C 中的简化系统的模型，我们引入了图4中系统状态变量集合。 $\theta$ 表示机器人向前倾斜的角度，$\upsilon$ 表示平面上的线性速度，$\omega$ 表示普通的角速度。机器人腿部位置是通过侧身倾角 $\beta$ （当前仅仅用于在章节Ⅵ介绍的实验性倾斜模式），$h$ 为到机器人等效质心的高度。对于里程方面，我们使用$x$，$y$，和$\gamma$ 作为平面坐标系下的位置以及方向参数，使用$s$ 作为在平面上行驶的距离。

我们更进一步引入了广义坐标向量 $q=[\theta ,s,\gamma {]}^T$ ，并在 Ⅲ-C 中使用它对系统进行建模。使用LQR状态向量 $x=[\theta ,\dot{\theta },\upsilon ,\omega {]}^T$ 进行在章节 Ⅳ-A 中的稳定性反馈控制。

图4 广义坐标系下简化的Ascento机器人模型

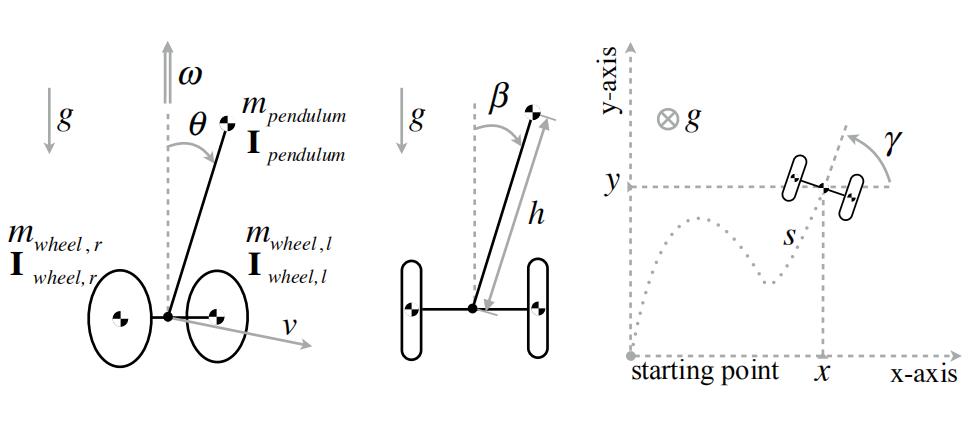
在对角线，后视以及俯视的图。我们使用 $m_{body}$ 代表质量，用 $I_{body}$ 表示惯量，其中对相应部件的描述作为名称的下标。$g$ 表示地球重力加速度。

B. 假设

为了减少建模难度并简化模型，我们做了如下假设：

1. 忽视腿部连接处的动力。
2. 假设是理想关节，没有摩擦以及滞后效果。
3. 轮子以及地面的摩擦简化为无滑动的情况。
4. 忽略电机动力学，假设它们远远比系统其余部分更快。
5. 不对系统延迟进行建模。
6. 所有的连杆以及机构都为刚体。

假设1表明了一个固定的髋关节电机，使得模型仅仅适用于一种特别的腿部结构。这个限制通过插补控制策略得到了解决，降低了在章节 Ⅳ 中有所描述的假设的重要程度。在章节Ⅴ中，其余假设可以顺利地被作为外部未知干扰来进行建模，并且可以被一个高效、快速、鲁棒性强的控制器所补偿。

C. 刚体模型

对于固定腿部几何的假设，可将机器人模型简化为特定高度的一个双轮倒立摆模型，这个模型包括三个部分：两个轮子以及一个结合了整个构件，有等效长度、惯量以及质心的倒立摆。使用空间速度传递公式[19]，并仅使用在章节 Ⅲ-A 介绍的广义坐标系对每个构件进行运动学建模。通过以上表述，可以分别推导出整个系统的动能以及势能，$T$ 和 $V$ ，并且代入拉格朗日函数

通过使用第一种拉格朗日等式来获取系统动力学方程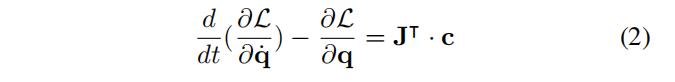

其中 $t$ 是持续的时间变量，$J$ 是系统的雅可比矩阵，$c$ 是外部笛卡尔力矢量。在$c$ 中，对于所有刚体的水平和垂直的力分量设置为零。力矩分量设定与特定电机以及扭簧对对应刚体所作用的力矩相同。

从等式2中，可以推导出所包含的运动方程，其中$M$ 是系统的质量矩阵，$f$ 是力。

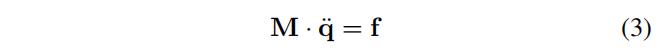
所有的系统参数，比如说长度，质量以及惯量，都是通过对所有零件准确的质量测量确定的，并且使用计算机辅助设计（CAD）的模型来进行计算，假设所有成分的密度都是恒定的。

Ⅳ 控制

双轮机器人天生是不稳定的。因此，不仅是跳跃，对于站立以及行驶也需要专门的控制策略。此外，进入操作模式或者从跌倒恢复也需要一个特殊的控制方法。

A. 稳定性控制

能够行驶、跳跃以及再次落地，并通过两轮维持直立，需要一个可靠的稳定算法。鲁棒性也是极为重要的。机器人应该能够处理外界干扰，同时使用尽可能小的空间来恢复平衡。使用的方法是LQR，是对于线性系统实现最小代价控制的最优化控制策略。Li，Yang和Fan[20]说明了LQR控制器可以为两轮倒立摆稳定系统有效地提供高可靠性以及鲁棒性。

LQR在有限问题下的最优化控制序列是通过解离散时间下的Riccati代数等式找到的。

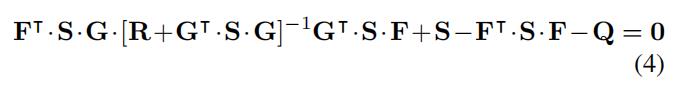
其中 $F$ 和 $G$ 是系统的离散时间状态空间表示矩阵，$Q$ 和 $R$ 是权重矩阵，$S$ 是等式中未知的矩阵。

最优化的反馈增益矩阵 $K$ 是

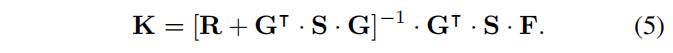
$Q$ 和 $R$ 是基于整个系统的每个状态以及期望的响应速度来选取的。为了简化这个过程，通过假设权重矩阵为对角矩阵，减少需要调整的权重参数到6个。为了整定这些数值，在真实系统上进行了复杂的测试。

LQR状态向量选择为 $x=[\theta ,\dot{\theta },\upsilon ,\omega {]}^T$ ，忽略了空间位姿以及方向。对于这个选择，背后的考虑是将位置跟踪问题留给一个专门的控制器，使其给予LQR速度命令。当这个控制器操控机器人时，在状态向量被控制器使用前，一个参考点将会添加到状态向量的 $v$ 或者 $\omega$ 中，以此来控制机器人达到一个特定的目标速度。

考虑到膝部角度的变化，将动力学方程线性化到十个不同的，等距的腿部高度。这通过线性插值法，产生了十个次序的状态空间模型以及相应的反馈增益矩阵K。因此，在 Ⅲ-B 假设1中引入的简化模型的限制就可以得到解决。

这个系统通过LQR控制法来调整

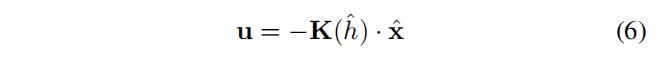
输入向量u包括左轮以及右轮的力矩，$h$ ̂在增益矩阵作为线性插值使用。这里 $x$ ̂和 $h$ ̂是直接通过 Ⅱ-C 中描述的状态观测器获取得到。根据分离原则，这个估计以及控制器设定是保证稳定的，并且能够使得只要噪声、干扰、建模错误以及制动器饱和对于系统的动力学没有影响，机器人就能回到其最佳的直立平衡位姿。

B. 跳跃控制

跳跃控制器的激活会使用一个预定义的跳跃序列来接管当前的行驶控制器并且对机器人进行完全的控制。跳跃控制器是一个启发式的前馈控制器，受到人类跳跃的运动的启发，具有分离的一系列的相位（图5）。在下面的部分，对跳跃行为所需要的各个跳跃相位进行了更加详细的描述

图5 跳跃序列的分离相位

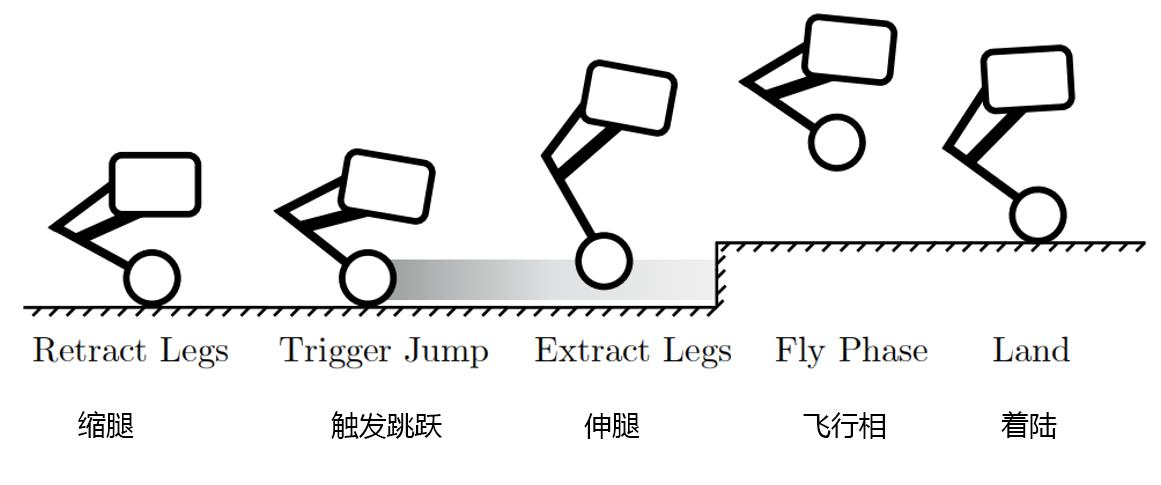
（在每个相位都使用了不同的控制器策略。）

1. 缩腿：使用一个控制器，来沿着腿部电机的一个特定的轨迹，使得机器人的腿可以收缩。在这个过程中，稳定性控制器是工作的。
2. 触发跳跃：当高度变化，名义上达到稳定后，机器人获得一个向前的速度。使用ToF距离传感器，当到达这一步的一个预定义的距离时，触发接下来的腿部伸展。
3. 伸腿：使用比例积分微分（PID）控制器来调节同步伸展，使用两个髋关节电机来伸展腿部。一旦腿部完全伸展后，稳定控制器失效，并且失去与地面的接触。
4. 飞行相：在髋关节电机上使用一个PID位置环使得到达收缩的腿的位置。以此来模拟一个虚拟弹簧减震器。这个行为无论是跨越高障碍物还是防止轮子触及台阶边缘都很有效。
5. 着陆：当髋关节关节的力矩超过一个特定的阈值时检测到触地。当检测到触地时，稳定性控制恢复。髋关节电机再一次模拟虚拟弹簧减震器，使得能够有一个平滑的能量缓冲以及可控的着陆。

用户可以通过一个图形化用户接口（GUI）来设定跳跃高度以及向前的速度。这可以为不同的场景调节跳跃相位的参数，比如说在一个点跳跃、行驶时跳跃以及跳跃上台阶。

C. 倒地恢复控制

当跌倒后或者在启动时，机器人不在它的直立状态。站立的过程可以从四个静止的位姿中的三个实施（图6）[21]。此外，系统可以以可控的方式来进入这些静止状态。

图6 四种机器人可能会跌倒的所有稳定位姿

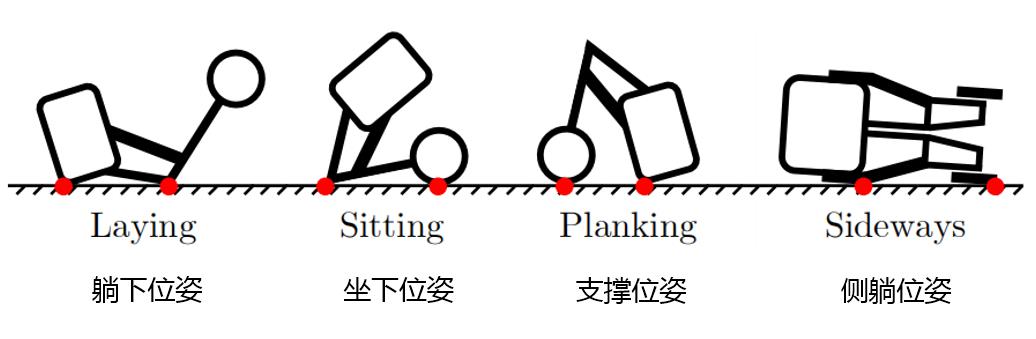
（机器人与地面的接触点使用红点标注出。）

静止位姿是通过机器人与地面之间的接触点所定义的。在躺下的位姿，机器人用腿部以及身体的后部接触地面。坐下的位姿中，它通过轮子以及腿部接触地面，在支撑位姿，使用身体的前部以及轮子接触地面。当机器人侧身躺下，使用一个单腿以及单个轮子接触地面时（侧躺位姿），它既不能恢复也不能通过受控的方式到达这个静止位姿。

与跳跃过程相似，站立过程也是由离散的一系列的相位组成，且对于所有静止位姿都很相似。这个活动由用户触发并会接管当前的行驶控制器。

图7 站立过程的相位

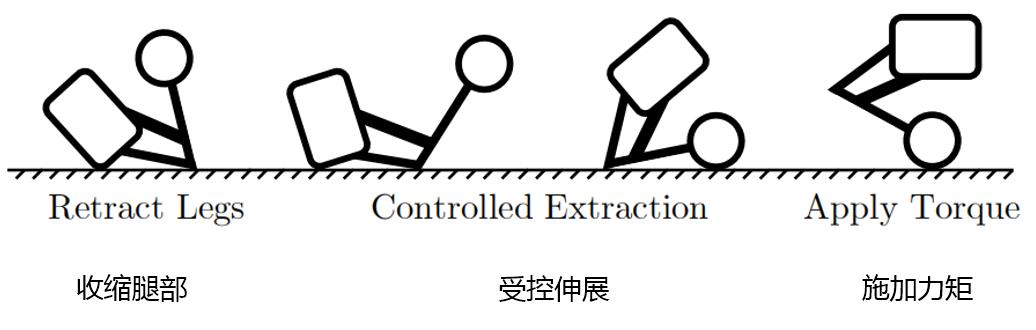
（受控的伸展步骤仅仅在躺下位姿中使用。）

1. 收缩腿部：使用控制器来使髋关节电机遵循一个特定的轨迹，让机器人的腿部收缩。
2. 受控伸展：这一步仅仅应用于躺下的位姿。遵循一个预定义的轨迹，腿部会伸展并稍后再次收缩。这引起了膝关节部分的旋转，使机器人到达坐下的位姿。一个受控的腿部伸展如果伸展地过快会使得机器人腾空并导致一个较强的撞击。另一方面，太慢的伸展会使得机器人的倾斜程度不足以到达坐下的位姿。
3. 施加力矩：给轮子电机施加一个持续的力矩，对于坐下的位姿向后，对于支撑位姿则向前。一直施加持续力矩，直到机器人有足够的旋转能量到达零倾斜角。一旦机器人站直了，稳定控制器就会开启，机器人会刹车来到达它理想的直立位姿。

使用受控的方式进入静止位姿是通过关闭稳定控制器以及对轮子电机施加一个微小的力矩来控制倒地的方向。

双足轮开源技术交流QQ群：543613782

参与翻译者：灯哥开源团队，华侨大学华机战队

原文论文： A Two-Wheeled Jumping Robot ——Victor Klemm∗, Alessandro Morra∗, Ciro Salzmann∗, Florian Tschopp, Karen Bodie,Lionel Gulich, Nicola Küng, Dominik Mannhart, Corentin Pfister, Marcus Vierneisel,Florian Weber, Robin Deuber, and Roland Siegwart，2019 ICRA