计算图的最短距离--Dijkstra算法

Posted 2021-07-12 C_YCBX Py_YYDS

文章目录

• (也就5min)先点开链接把Dijkstra算法过程看一看(否则肯定看不懂代码).
• 详解代码实现过程(请结合视频过程分析)
• • 用到的基本数据表示
  • 各个函数模块实现(重在Dijkstra函数)
• 以题代讲--具体实现
• • 蓝桥杯--文化之旅
  • 解题过程
  • 汇总代码提交

(也就5min)先点开链接把Dijkstra算法过程看一看(否则肯定看不懂代码).

视频详解Dijkstra算法过程

此方法最短路径的适用范围：单源带权图，要是不带权完全可以用bfs。

---

详解代码实现过程(请结合视频过程分析)

用到的基本数据表示

根据视频中讲解的实现原理，我们需要通过多个数组来实现该过程。

1. dist[i]数组(下标表示第几个结点)用于标记起点S到i的最短距离，初始值全为无穷大，这个值只要足够大就行。
2. visit[i]数组(下标同上)用于标记每个已经得到最短距离的结点，初始值全为false,表示该结点还未找到最短距离。
3. path[i]数组(下标同上)用于标记每个已经得到最短距离的结点的前驱(最短路径中的上一个结点)，初始值全为-1。
4. Graph[i][j]这是一个带权矩阵，表示任意i结点到j结点间边的距离,若两者间无边则初始为无穷大。

---

各个函数模块实现(重在Dijkstra函数)

• init()

void init()//在读入数据之前初始化图
{//Graph和dist在读取数据之前都初始化为INF，path初始化为-1
    for(int i = 1; i <= N; i++){
        path[i] = -1;
        dist[i] = INF;
        for(int j = 1; j <= N; j++){
            Graph[j][i] = INF;//INF为自定义的较大的值
        }
    }
    memset(visit,0,sizeof(visit));//起初，没有一个结点被标记
}

• FIndMin()

int FindMin()//找出未被visit标记的结点中最小的距离结点,并返回该结点
{
    int minV = S;//初始为S，如果未被更新则路径更新过程结束
    int minDist = INF;
    for(int i = 0; i < N; i++){
        if(!visit[i] && dist[i] < minDist){//没有被标记&&距离最小
            minV = i;
            minDist = dist[i];
        }
    }//返回没有被标记的最小结点
    return minV;
}

• Dijkstra()

void Dijkstra()
{//S表示起点，T表示终点
    dist[S] = 0;//起点到自己的距离设为0
    visit[S] = true;//将起点标记
    for(int i = 1; i <= N; i++){
    //更新与起点S相连的结点的距离值
        int t = Graph[i][S];
        if(t < INF){
			dist[i] = t;
			path[i] = S;
		}      
    }
//要么无法到达，要么就是找到到达终点的最小值，否则一直循环。
    while(1){
    //得到未被标记的最小结点，将其标记
        int v = FindMin();
        if(v==S)//如果未被更新，则无需再更新了，要么全被标记，要么就是剩下的无法到达
            return;
        visit[v] = true;//将该结点标记
        if(visit[T])return;//一旦T被标记，则说明到达终点的最小值已经找到
        for(int i = 1; i <= N; i++){
        //这个结合视频的更新过程想想就懂了
            if(!visit[i]&&Graph[v][i]!=INF){//没被标记&&两者之间存在边
                if(dist[v] + Graph[v][i] < dist[i]){
                    dist[i] = dist[v] + Graph[v][i];
                    path[i] = v;
                }
            }
        }
    }
}

---

以题代讲–具体实现

蓝桥杯–文化之旅

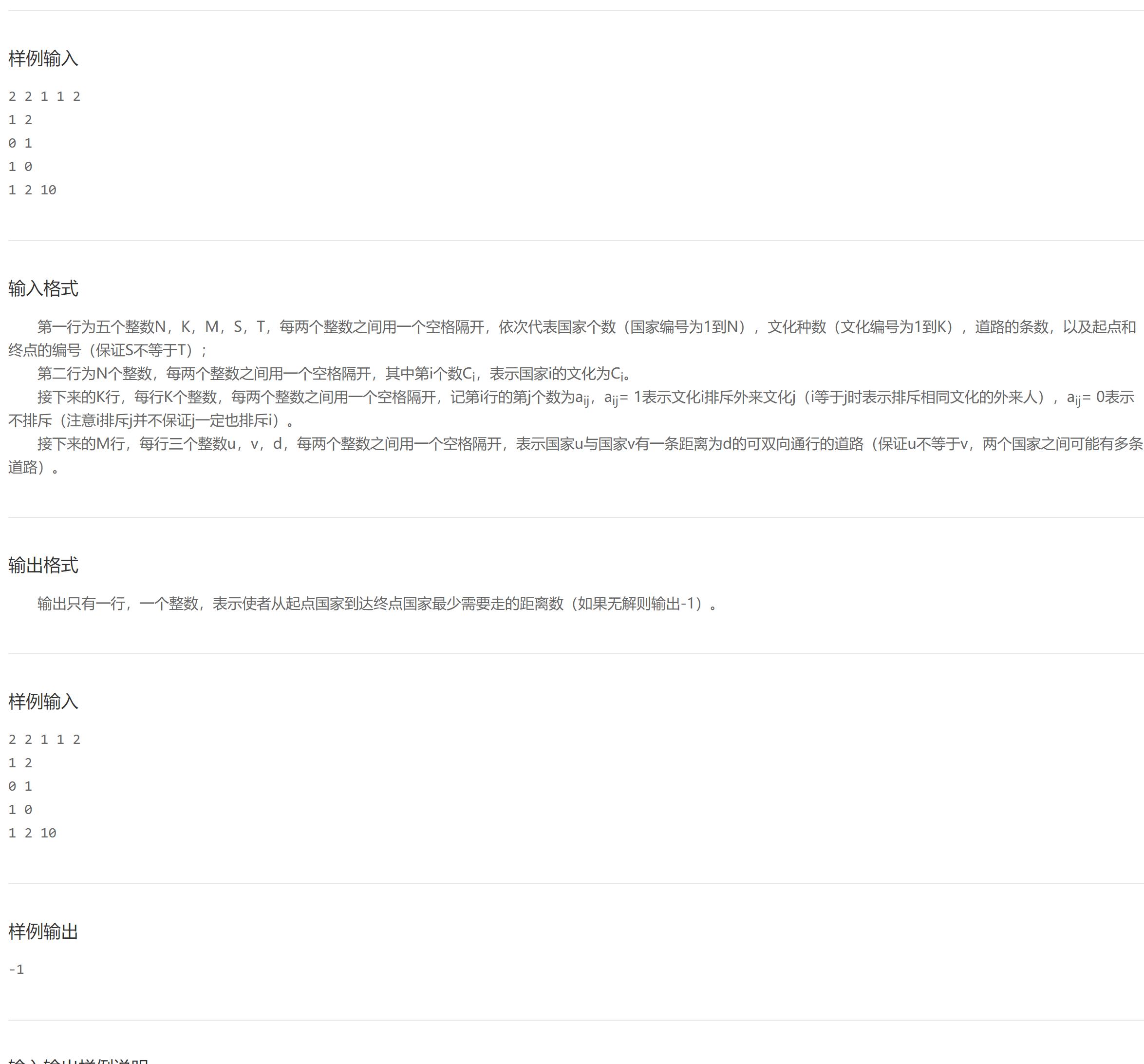
看完题目，唯一的区别在于还需要额外判断文化是否排斥，这个在函数中多添加一个判断条件就行。

解题过程

我们按照上述的过程三步走试试：

• 初始化过程(我比较习惯用vector容器所以就没有单独写init函数了)

//vector容器的初始化方法--vector<类型>变量名(长度,初始值);
const int size = 505;//用于初始化一个size长度的数组
vector<int>path(size,-1);
vector<int>dist(size,INT_MAX);
vector<bool>visit(size,false);
vector<vector<int> >Graphics(size,vector<int>(size,INT_MAX));
//下面两个是本题新加的属性，我们建立所属文化以及文化关系数组来存储。
vector<int>cultures(size);
bool cultureLinks[size][size] = {false};

• 找最小结点的函数FindMin()

int FindMin()
{
    int minV = S;
    int minDist = INT_MAX;
    for(int i = 1; i <= N; i++){
        if(!visit[i] && dist[i] < minDist){
            minV = i;
            minDist = dist[i];
        }
    }
    return minV;
}

• Dijkstra() 函数

void Dijkstra()
{
    dist[S] = 0;
    visit[S] = true;
    for(int i = 1; i <= N; i++){
        int t = Graphics[S][i];
        if(t < INT_MAX&&!cultureLinks[cultures[i]][cultures[S]]){
           dist[i] = t; path[i] = S;}
    }
    while(1){
        int v = FindMin();
        if(v==S) return;
        visit[v] = true;//将此次最小路径结点标记
        //一旦T终点被标记则说明答案已经出现
        if(visit[T])return;
        for(int i = 1; i <= N; i++){
            if(!visit[i]&&Graphics[v][i]!=INT_MAX&&!cultureLinks[cultures[i]][cultures[v]]){//只有结点未被标记 && 文化不会排斥 && 路径长度不是无穷大
                if(dist[v] + Graphics[v][i] < dist[i]){
                    dist[i] = dist[v] + Graphics[v][i];
                    path[i] = v;
                }
            }
        }
    }
}

• main函数测试接口

int main(){
cin>>N>>K>>M>>S>>T;
for(int i=1;i<=N;i++)
    cin>>cultures[i];
for(int i=1;i<=K;i++)
    for(int j=1;j<=K;j++)
        cin>>cultureLinks[i][j];
for(int i=1;i<=M;i++){
        int u,v,d;cin>>u>>v>>d;//无向图
        Graphics[u][v] = Graphics[v][u] = d;
}
Dijkstra();
if(dist[T]!=INT_MAX)
    cout<<dist[T];
else
    cout<<-1;
return 0;
}

汇总代码提交

#include<bits/stdc++.h>
using namespace std;
const int size = 505;
vector<int>path(size,-1);
vector<int>dist(size,INT_MAX);
vector<bool>visit(size,false);
vector<vector<int> >Graphics(size,vector<int>(size,INT_MAX));
vector<int>cultures(size);
bool cultureLinks[size][size] = {false};
int N,K,M,S,T;

int FindMin()
{
    int minV = S;
    int minDist = INT_MAX;
    for(int i = 1; i <= N; i++){
        if(!visit[i] && dist[i] < minDist){
            minV = i;
            minDist = dist[i];
        }
    }
    return minV;
}

void Dijkstra()
{
    dist[S] = 0;
    visit[S] = true;
    for(int i = 1; i <= N; i++){
        int t = Graphics[S][i];
        if(t < INT_MAX&&!cultureLinks[cultures[i]][cultures[S]]){
           dist[i] = t; path[i] = S;}
    }
    while(1){
        int v = FindMin();
        if(v==S) return;
        visit[v] = true;//将此次最小路径结点标记
        //一旦T终点被标记则说明答案已经出现
        if(visit[T])return;
        for(int i = 1; i <= N; i++){
            if(!visit[i]&&Graphics[v][i]!=INT_MAX&&!cultureLinks[cultures[i]][cultures[v]]){//只有结点未被标记 && 文化不会排斥 && 路径长度不是无穷大
                if(dist[v] + Graphics[v][i] < dist[i]){
                    dist[i] = dist[v] + Graphics[v][i];
                    path[i] = v;
                }
            }
        }
    }
}

int main(){
cin>>N>>K>>M>>S>>T;
for(int i=1;i<=N;i++)
    cin>>cultures[i];
for(int i=1;i<=K;i++)
    for(int j=1;j<=K;j++)
        cin>>cultureLinks[i][j];
for(int i=1;i<=M;i++){
        int u,v,d;cin>>u>>v>>d;//无向图
        Graphics[u][v] = Graphics[v][u] = d;
}
Dijkstra();
if(dist[T]!=INT_MAX)
    cout<<dist[T];
else
    cout<<-1;
return 0;
}