提高篇：图的最短路径算法和最小生成树算法

Posted 2021-04-28 小文学编程

Dijkstra 最短路径算法

操作步骤

通过Dijkstra 计算图G中的最短路径时，需要指定起始点vs(即从顶点vs开始计算）。此外，引进两个集合s和u，s的作用是记录已经求出最短路径的顶点，而u则是记录还未求出最短路径的顶点(以及该顶点到起点vs的距离）

（1）初始时，S只包含起点vs，U包含除了vs 外的其他顶点，且u中的顶点的距离为“起点vs到该顶点的距离“【例如：u中顶点v的距离为（vs，v）的长度，然后vs 和v相邻，则v的距离 为 正无穷】

（2）从U中选出“距离最短的顶点k”，并将顶点k加入到s中，同时，从u中移除顶点k

（3）更新u中各个顶点到起点的vs的距离，之所以更新u中顶点的距离，是由于上一步中确定了k是求出最短路径的顶点，从而可以利用k来更新其他顶点的距离。例如，（vs，v）的距离可能大于（vs，k）+（k，v）的距离

（4）重复步骤 2 和 3 ，知道遍历完所有顶点

代码实操

例子：计算下图起始定点到各个顶点的最短路径

//Dijkstra 最短路径算法
public class ShortPathDijkstra {
    //邻接矩阵
    private int[][] matrix;
    //表示正无穷
    private int MAX_LENGTH = Integer.MAX_VALUE;
    //顶点集合
    private String[] vertexes;
    /**
     * 创建图
     * @param index
     */
    public void createGraph(int index){
        matrix = new int[index][index];
        vertexes = new String[index];

        int[] v0 = {0,1,5,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH};
        int[] v1 = {1,0,3,7,5,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH};
        int[] v2 = {5,3,0,MAX_LENGTH,1,7,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH};
        int[] v3 = {MAX_LENGTH,7,MAX_LENGTH,0,2,MAX_LENGTH,3,MAX_LENGTH,MAX_LENGTH};
        int[] v4 = {MAX_LENGTH,5,1,2,0,3,6,9,MAX_LENGTH};
        int[] v5 = {MAX_LENGTH,MAX_LENGTH,7,MAX_LENGTH,3,0,MAX_LENGTH,5,MAX_LENGTH};
        int[] v6 = {MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,3,6,MAX_LENGTH,0,2,7};
        int[] v7 = {MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,9,5,2,0,4};
        int[] v8 = {MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,MAX_LENGTH,7,4,0};

        matrix[0] = v0;
        matrix[1] = v1;
        matrix[2] = v2;
        matrix[3] = v3;
        matrix[4] = v4;
        matrix[5] = v5;
        matrix[6] = v6;
        matrix[7] = v7;
        matrix[8] = v8;

        vertexes[0] = "v0";
        vertexes[1] = "v1";
        vertexes[2] = "v2";
        vertexes[3] = "v3";
        vertexes[4] = "v4";
        vertexes[5] = "v5";
        vertexes[6] = "v6";
        vertexes[7] = "v7";
        vertexes[8] = "v8";
    }

    /**
     * Dijkstra 最短路径算法
     * vs --起始顶点(start vertex),即，统计图中 顶点vs 到其他各个顶点的最短路径
     * @param vs
     */
    public void dijkstra(int vs){
        //flag[i] = true 表示顶点 到 顶点 i 的最短路径已经成功获取
        boolean[] flag = new boolean[vertexes.length];
        //u是 记录 还未求出最短路径的顶点（以及该顶点到起点s的距离，与falg 配合使用，flag[i] == true 表示u中i顶点已被移除）
        int[] u = new int[vertexes.length];
        // 前驱顶点数组，即perv[i] 的值是"顶点vs"到顶点i的最短路径锁经历的全部顶点中，位于顶点i之间的那个顶点
        int[] prev = new int[vertexes.length];
        //s的作用是记录已经求出最短路径的顶点
        String[] s = new String[vertexes.length];

        //步骤1 ，初始时，s中只有起点vs，u中除vs之外的顶点，并且u中顶点的路径是 起点vs 到该顶点的路径
        for(int i=0;i<vertexes.length;i++){
            flag[i] = false;//顶点i 的最短路径还没有获取到
            u[i] = matrix[vs][i];//顶点i 与顶点 vs的初始距离为 顶点 vs 到顶点i的权，也就是 邻接矩阵 vs 行的数据

            prev[i] = 0;//顶点 i 的前驱顶点 为 0
        }

        //将vs 从u 中 移出 （u与flag 配合使用）
        flag[vs] = true;
        u[vs] = 0;
        //将 vs 顶点 加入 s
        u[vs] = 0;
        s[0] = vertexes[vs];
        //步骤1 结束
        
        //步骤四：重复步骤2,3，直到遍历完所有的顶点
        //遍历 vertexes.length -1次，每次找出一个顶点的最短路径
        int k =0;
        for(int i=1;i<vertexes.length;i++) {
            //步骤2：从U中 找出路径最短的顶点，并将其加入到S中（如果vs顶点 到x 顶点还有更短的路径的haul，那么必然会有一个y顶点到vs顶点
            // 的路径币前者更短且没有加入s中，所以u中路径最短顶点的路径就是该顶点的最短路径）
            //即，在未获取最短路径的顶点中，找到离vs最近的顶点k
            int min = MAX_LENGTH;
            for (int j = 0; j < vertexes.length; j++) {
                if (flag[j] == false && u[j] < min) {
                    min = u[j];
                    k = j;
                }
            }
            //将k 加入s中
            s[i] = vertexes[k];
            //步骤2结束

            //步骤三，更新u中的顶点和顶点对应的路径
            //标记 顶点k 为已经获取到最短路径（更新u中的 顶点，即将k 顶点对应的flag 标记为 true）
            flag[k] = true;

            //修正当前 最短路径和前驱顶点（更新u中剩余顶点对应的路径）
            //即，当已经 顶点 k 的最短路径之后 更新 未获取最短路径的顶点的最短路径和前驱顶点
            for (int j = 0; j < vertexes.length; j++) {
                //以k 顶点 所在位置连线其他顶点，判断其他顶点经过最短路径顶点k 到达 vs 顶点是否小于 目前的最短路径，是，更新入u，不是不做处理
                int tmp = (matrix[k][j] == MAX_LENGTH ? MAX_LENGTH : (min + matrix[k][j]));
                if (flag[j] == false && (tmp < u[j])) {
                    u[j] = tmp;
                    //更新j 顶点 的最短路径 前驱顶点为k
                    prev[j] = k;
                }
            }
            //步骤三结束
        }
        //步骤四结束
        //打印Dijkstra 最短路径结束
        System.out.println("起始顶点："+ vertexes[vs]);
        for(int i=0;i<vertexes.length;i++){
            System.out.print("最短路径（"+ vertexes[vs] + "," + vertexes[i] + "):"+ u[i]+ " ");
            List<String> path = new ArrayList<>();
            int j=i;
            while (true){
                path.add(vertexes[j]);
                if(j == 0){
                    break;
                }
                j = prev[j];
            }
            for(int x= path.size() -1 ; x>=0;x--){
                if(x == 0){
                    System.out.println(path.get(x));
                }else{
                    System.out.print(path.get(x) + " -> ");
                }
            }
        }
        System.out.println("顶点放入到s中的顺序");
        for(int i=0; i < vertexes.length;i++){
            System.out.print(s[i]);
            if(i != vertexes.length){
                System.out.print("-->");
            }
        }
    }
    public static void main(String[] args) {
        ShortPathDijkstra shortPathDijkstra = new ShortPathDijkstra();
        shortPathDijkstra.createGraph(9);
        shortPathDijkstra.dijkstra(0);
    }
}

结果：

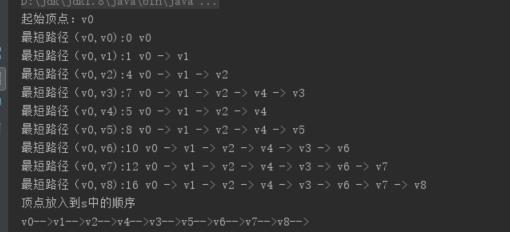
最小生成树算法

基本概念

在含有n个顶点的连通图中选择n-1 条边，构成一棵 极小连通子图，并且使连通子图中n-1条边上权值和达到最小，则称其为连通网的最小生成树。

计算的例子

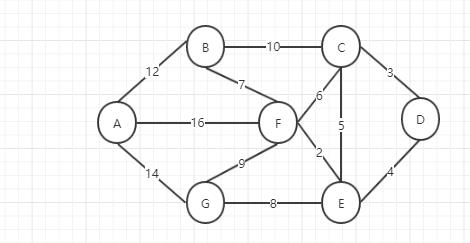
用邻接表构造图：

private int mEdgNum; //边的数量
private char[] mVexs;//顶点集合
private int[][] mMatrix;//邻接矩阵
private static final int INF = Integer.MAX_VALUE;

public SmallestTree(char[] vexs,int[][] matrix){
    //初始化 顶点是和 边数
    int vlen = vexs.length;

    //初始化 顶点
    mVexs = new char[vlen];
    for(int i=0;i<mVexs.length;i++){
        mVexs[i] = vexs[i];
    }

    //初始化边
    mMatrix = new int[vlen][vlen];
    for(int i=0;i<vlen;i++){
        for(int j=0;j<vlen;j++){
            mMatrix[i][j] = matrix[i][j];
        }
    }
    //统计边
    mEdgNum = 0;
    for(int i=0;i<vlen;i++){
        for(int j = i+1 ; j<vlen ;j++){
            if(mMatrix[i][j] != INF){
                mEdgNum++;
            }
        }
    }
}

/**
 * 返回ch的位置
 * @param ch
 * @return
 */
private int getPosition(char ch){
    for(int i=0;i<mVexs.length ; i++){
        if(mVexs[i] == ch){
            return i;
        }
    }
    return -1;
}

/**
 * 打印矩阵队列图
 */
public void print(){
    System.out.printf("Matrix Graph:\n ");
    for (int i=0;i<mVexs.length;i++){
        for(int j=0;j<mVexs.length;j++){
            System.out.printf("%10d",mMatrix[i][j]);
        }
        System.out.println();
    }
}

Prime算法

基本思想：对于图而言，V是所有顶点的集合。现在设置两个新的的集合U和T，其中U用于存放图中最小生成树的顶点，T存放图的最小生成树中的边。从所有  u属于U  v属于（V-U） 【V-U 表示除去U的所有顶点】 的边中选取权值最小的边（u,v）,将顶点 v 加入集合 U中，将边（u,v） 加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

/**
 * prime 最小生成树算法
 * @param start
 */
public void prim(int start){
    int num = mVexs.length; //顶点个数
    int index = 0; //prime 最小树的索引，即prime 数组的索引
    char[] prims = new char[num];//prime 最小树 的结果数组
    int[] weights = new int[num];//顶点间边的权值

    //prime 最小生成树 中第一个数 是 图中第 start个顶点， 因为是从start 开始的
    prims[index++] = mVexs[start];

    //初始化 顶点的权值数组
    //将每个顶点的权值初始化为 第 start 个 顶点 到该顶点的权值
    for (int i=0;i<num ;i++){
        weights[i] = mMatrix[start][i];
    }
    //将第start 个顶点的权值初始化为0
    //可以理解为 第 start 个 顶点到其它自身的距离为0
    weights[start] = 0;

    for (int i=0;i<num ; i++){
        //由于从start 开始 的，因此不需要再对 第start 个 顶点进行处理
        if(start == i){
            continue;
        }
        int j= 0;
        int k  =0;
        int min = INF;
        //在未被加入到最小生成树的顶点中，找出权值最小的顶点
        while (j < num){
            //若 weights[j] = 0 .意味着 第 j 个顶点已经排序过了(或者已经加入到最小生成树中了)
            if(weights[j] != 0 && weights[j] <min){
                min = weights[j];
                k = j;
            }
            j++;
        }

        //经过上面的处理后，在未被加入到最小生成树的顶点，权值最小的顶点是第k个顶点
        //将第k个顶点加入到最小生成树的结果数组中
        prims[index++] = mVexs[k];
        //将 第k个顶点加入到最小生成树的结果数组中
        weights[k] = 0;
        //当第k 个 顶点 被加入到最小生成树 的结果数组中之后，更新其他顶点的权值
        for(j = 0;j<num ;j++){
            //将 第j 个顶点 被加入到 最小生活树的结果数组之中，更新其他顶点的权值
            if(weights[j] != 0 && mMatrix[k][j] < weights[j]){
                weights[j] = mMatrix[k][j];
            }
        }
    }

    //计算最小生活树的权值
    int sum = 0;
    for(int i =1;i<index ; i++){
        int min =INF;
        //获取 prims[i] 在mMatrix 中的位置
        int n = getPosition(prims[i]);
        // 在 vexs[0...i]中 ，找出 到j的权值最小的顶点
        for(int j = 0;j<i;j++){
            int m = getPosition(prims[j]);
            if(mMatrix[m][n] < min){
                min = mMatrix[m][n];
            }
        }
        sum += min;
    }

    //打印最小生成树
    System.out.printf("PRIM(%c) = %d",mVexs[start],sum);
    for(int i =0;i<index;i++){
        System.out.printf("%c",prims[i]);
    }
    System.out.println();
}
//测试
    public static void main(String[] args) {
        char[] vexs = {'A','B','C','D','E','F','G'};
        int matrix[][] = {
                {0,12,INF,INF,INF,16,14},
                {12,0,10,INF,INF,7,INF},
                {INF,10,0,3,5,6,INF},
                {INF,INF,3,0,4,INF,INF},
                {INF,INF,5,4,0,2,8},
                {16,7,6,INF,2,0,9},
                {14,INF,INF,INF,8,9,0},
        };
        SmallestTree smallestTree;

        smallestTree = new SmallestTree(vexs,matrix);

        smallestTree.prim(0);
        smallestTree.kruskal();

    }

结果：

最小生成树的权重:36

Kruskal算法

基本思想：按照权值从小到大的顺序选择n-1条边，并保证 n-1 条边不构成回路。

具体做法：首先构造一个只含有n个顶点的森林。然后依照权值从小到大从连通图中选择边加入到森林中，并使得森林中不产生回路，直至森林变成一棵树为止。

/**
 * kruskal 最小生成树算法
 */
public void kruskal(){
    int index = 0; //rets 数组的索引
    int[] vends = new int[mEdgNum];//用于保存 “已有最小生成树”中每个顶点在该最小树中的终点
    EData[] rets = new EData[mEdgNum]; //结果数组，保存kruskal 最小生成树的边
    EData[] edges;

    //获取图中所有的边
    edges = getEdges();
    //将边按照权的大小进行排序
    edges = sortEdges(edges,mEdgNum);

    for (int i=0; i< mEdgNum ; i++){
        int p1 = getPosition(edges[i].start);//获取 第 i 条边的起点的序号
        int p2 = getPosition(edges[i].end); //获取第i条边的终点的序号

        int  m = getEnd(vends,p1); //获取 p1 在 已有的最小生成树中的终点
        int  n = getEnd(vends,p2);//获取p2 在已有的最小生成树中的终点

        //如果 m != n 意味着 边i 与 已经添加到最小生成树中的顶点没有形成环路
        if(m != n){
            vends[m] = n;//设置 m 在已有的最小生成树 中的终点位n
            rets[index++] = edges[i];// 保存结果
        }
    }

    //统计 并打印 kruskal 最小生成树的信息
    int length = 0;
    for(int i=0;i<index;i++){
        length += rets[i].weight;
    }
    System.out.printf("Kruskal=%d",length);
    for(int i = 0 ;i<index ; i++){
        System.out.printf("(%c,%c)",rets[i].start,rets[i].end);
    }
    System.out.println();
}

private static class EData{
    char start;
    char end;
    int weight;

    public EData(char start,char end,int weight){
      this.start = start;
      this.end = end;
      this.weight = weight;
    }
}

/**
 * 获取i的终点
 * @param vends
 * @param i
 * @return
 */
private int getEnd(int[] vends,int i){
    while (vends[i] != 0){
        i = vends[i];
    }
    return i;
}

private EData[] sortEdges(EData[] edges,int elen){
    for(int i=0;i<elen;i++){
        for (int j=i+1; j<elen;j++){
            if(edges[i].weight > edges[j].weight){
                EData temp = edges[i];
                edges[i] = edges[j];
                edges[j] = temp;
            }
        }
    }
    return edges;
}

private EData[] getEdges(){
    int index = 0;
    EData[] edges;

    edges = new EData[mEdgNum];
    for(int i=0;i< mVexs.length ;i++){
        for(int j=i+1;j <mVexs.length;j++){
            if(mMatrix[i][j] != INF){
                edges[index++] = new EData(mVexs[i],mVexs[j],mMatrix[i][j]);
            }
        }
    }
    return edges;
}

结果：

最小生成树的权重为：36敬请关注！