神经网络与深度学习笔记激活函数与参数初始化

Posted 2021-07-07 沧夜2021

激活函数

为什么使用激活函数？

线性激活函数一般用于输出。如果使用线性方程，而不使用激活函数，那么神经网络不管多少层，它的输出就仅仅是输入函数的线性变化

ReLu

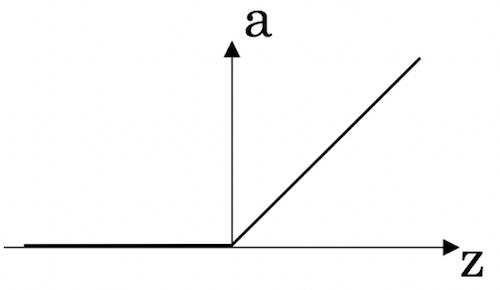
又称为整流线性单元函数，表达式可以表示为：
$$a=max(0,z)$$
ReLU函数一般可以默认使用，不知道用啥可以使用ReLU试试先。

ReLU函数在 $z>0$ 时，导数为1

$z<0$ 时，导数为0

leaky ReLU

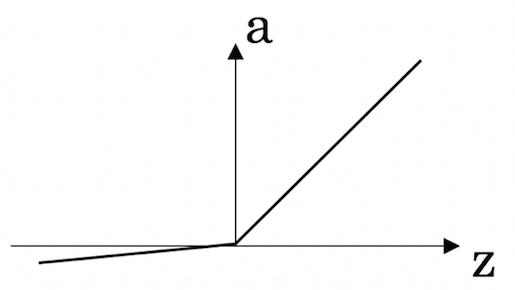
表达式可以表示为：
$$a=max(0.01z,z)$$
使用较少，与ReLU不同之处在于，当 $z<0$ 时，leaky ReLU，导数不为0

sigmoid

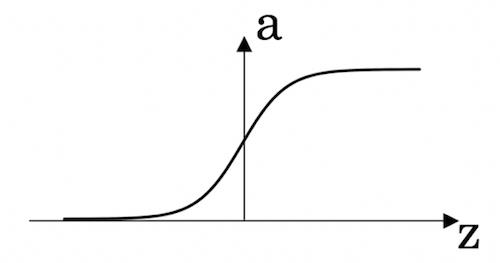
主要用于二元分类，表达式为：
$$a=\frac{1}{1+e^{-z}}$$
除非是二元分类或输出层。其他的情景不建议用。或许使用tanh更好

tanh

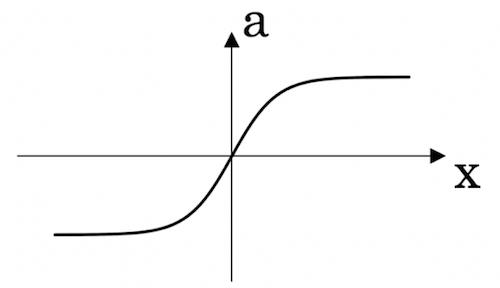
双曲正切函数，表达式为：
$$a=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$
一般情况下，tanh优于sigmoid，且具有居中数据的功能。

tanh 与 sigmoid 在 x 很大或者很小时，斜率接近0，会减缓梯度下降的速度

如果不知道哪种激活函数的效果好，不妨都试一遍！

参数初始化

对于参数 $w$ 我们不能初始化为0，因为那会出现对称失效的现象。当训练时， $a_1^1=a_2^1$ ，即 $a_1^1$ 与 $a_2^1$ 一致，这就使得隐藏层的功能一样，而不同隐藏层应该有不同的功能。同时，参数 $w$ 初始化为0在反向传播时，求得的导数也会是一样的。

因此，$w$ 应该使用随机初始化。

w1 = np.random.randn((2,2)) * 0.01	#当把0.01变成100时，在w增加，z增加的情况下，Z的梯度下降会变慢。

对于参数b 初始化为0时可以的。

检查矩阵维数

在检查神经网络是否会出现错误时，使用检查矩阵维数的方法是很有效的

我们设 $n^{[l]}$ 为第 $l$ 层的单元数

则它们的维数
$$w^{[l]},dw：(n^{[l]},n^{[l-1]})$$

$$b^{[l]},db：(n^{[l]},1)$$

$$z^{[l]},a^l:(n^{[l]},1)$$

$$Z^l,A^l,dZ,dA:(n^{[l]},m)$$

同时，在编程时候，记得将 $z^{[l]}$ 缓存起来，以便反向传播调用数据

例如：
输入 $a^{[l-1]}$

​输出 $a^l$，$Cache(z^{[l]},w^{[l]},b^{[l]})$

​输入 $d{a}^{[l]}$

​输出 $d{a}^{[l-1]},d{w}^{[l]},d{b}^{[l]}$
$$d{z}^{[l]}=d{a}^{[l]}\ast g^{[l{]}^{\prime }}(z^{[l]})$$

$$d{w}^{[l]}=d{z}^{[l]}\ast a^{[l-1]}$$

$$d{b}^{[l]}=d{z}^{[l]}$$

$$d{a}^{[l-1]}=w^{[l{]}^T}\ast d{z}^{[l]}$$