图解算法广度优先搜索

Posted 2021-07-02 learning吧

一、简介

广度优先搜索算法（Breadth-First Search，BFS）是一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。换句话说，它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。BFS并不使用经验法则算法。

 

广度优先搜索让你能够找出两样东西之间的最短距离，不过最短距离的含义有很多！使用广度优先搜索可以：

 

编写国际跳棋AI，计算最少走多少步就可获胜；

编写拼写检查器，计算最少编辑多少个地方就可将错拼的单词改成正确的单词，如将READED改为READER需要编辑一个地方；

根据你的人际关系网络找到关系最近的医生。

二、例子

假设你居住在旧金山，要从双子峰前往金门大桥。你想乘公交车前往，并希望换乘最少。可乘坐的公交车如下。

为找出换乘最少的乘车路线，你将使用什么样的算法？一步就能到达金门大桥吗？下面突出了所有一步就能到达的地方。

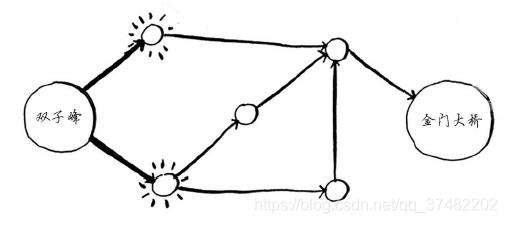
金门大桥未突出，因此一步无法到达那里。两步能吗？

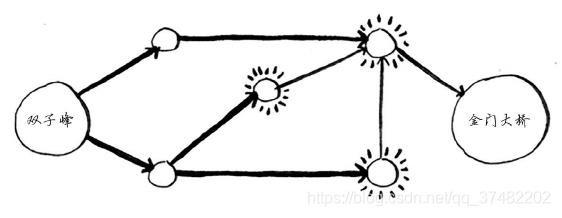
金门大桥也未突出，因此两步也到不了。三步呢？

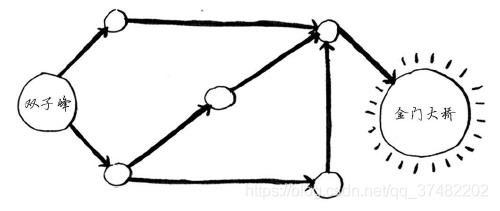
金门大桥突出了！因此从双子峰出发，可沿下面的路线三步到达金门大桥。

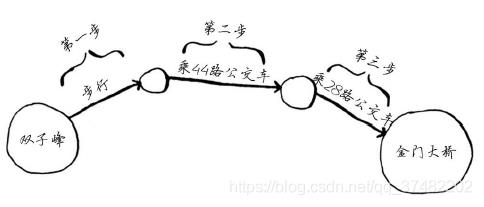
还有其他前往金门大桥的路线，但它们更远（需要四步）。这个算法发现，前往金门大桥的最短路径需要三步。这种问题被称为最短路径问题（shorterst-path problem）。你经常要找出最短路径，这可能是前往朋友家的最短路径，也可能是国际象棋中把对方将死的最少步数。解决最短路径问题的算法被称为广度优先搜索。要确定如何从双子峰前往金门大桥，需要两个步骤。

(1) 使用图来建立问题模型。

(2) 使用广度优先搜索解决问题。

下面介绍什么是图，然后再详细探讨广度优先搜索。

 

三、图

图是由顶点的有穷非空集合和顶点之间边的集合组成，通过表示为G(V,E)，其中，G标示一个图，V是图G中顶点的集合，E是图G中边的集合。

 

无边图：若顶点Vi到Vj之间的边没有方向，则称这条边为无项边（Edge），用序偶对(Vi,Vj)标示。

 

对于下图无向图G1来说，G1=(V1, {E1})，其中顶点集合V1={A,B,C,D}；边集合E1={(A,B),(B,C),(C,D),(D,A),(A,C)}:

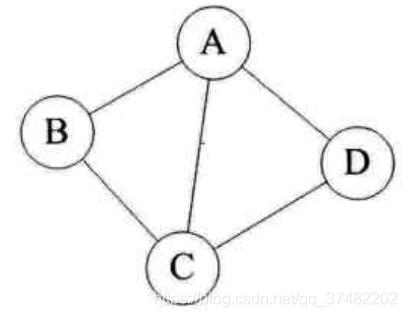
有向图：若从顶点Vi到Vj的边是有方向的，则成这条边为有向边，也称为弧（Arc）。用有序对（Vi，Vj）标示，Vi称为弧尾，Vj称为弧头。如果任意两条边之间都是有向的，则称该图为有向图。

 

有向图G2中，G2=（V2,{E2}），顶点集合（A,B,C,D）,弧集合E2={<A,D>,{B,A},<C,A>,<B,C>}.

 

权：有些图的边和弧有相关的数，这个数叫做权。这些带权的图通常称为网。

 

四、广度优先搜索算法

假设你经营着一个芒果农场，需要寻找芒果销售商，以便将芒果卖给他。在Facebook，你与芒果销售商有联系吗？为此，你可在朋友中查找。

这种查找很简单。首先，创建一个朋友名单。

然后，依次检查名单中的每个人，看看他是否是芒果销售商。

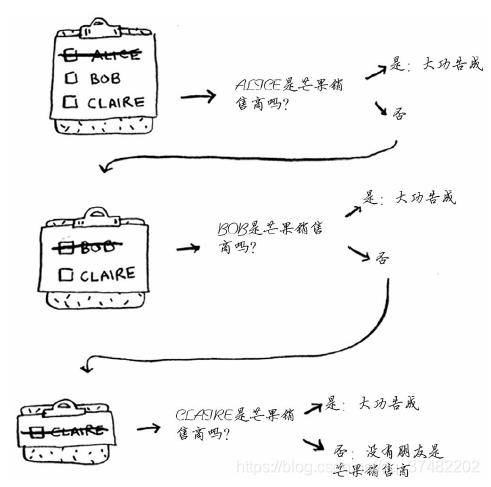
假设你没有朋友是芒果销售商，那么你就必须在朋友的朋友中查找。

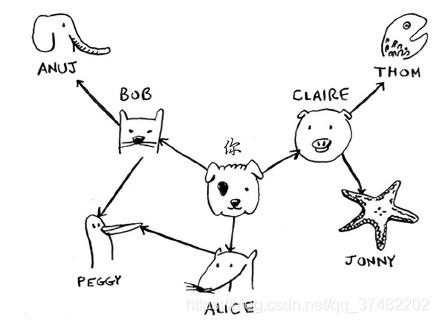
 检查名单中的每个人时，你都将其朋友加入名单。

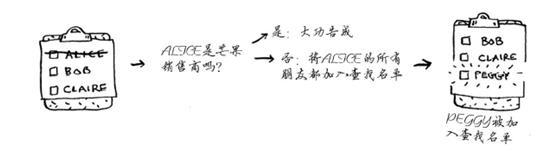
这样一来，你不仅在朋友中查找，还在朋友的朋友中查找。别忘了，你的目标是在你的人际关系网中找到一位芒果销售商。因此，如果Alice不是芒果销售商，就将其朋友也加入到名单中。这意味着你将在她的朋友、朋友的朋友等中查找。使用这种算法将搜遍你的整个人际关系网，直到找到芒果销售商。这就是广度优先搜索算法。

五、查找最短路径

再说一次，广度优先搜索可回答两类问题。

第一类问题：从节点A出发，有前往节点B的路径吗？（在你的人际关系网中，有芒果销售商吗？）

第二类问题：从节点A出发，前往节点B的哪条路径最短？（哪个芒果销售商与你的关系最近？）

刚才你看到了如何回答第一类问题，下面来尝试回答第二类问题——谁是关系最近的芒果销售商。例如，朋友是一度关系，朋友的朋友是二度关系。

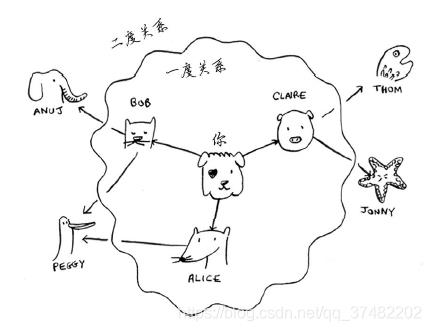
在你看来，一度关系胜过二度关系，二度关系胜过三度关系，以此类推。因此，你应先在一度关系中搜索，确定其中没有芒果销售商后，才在二度关系中搜索。广度优先搜索就是这样做的！在广度优先搜索的执行过程中，搜索范围从起点开始逐渐向外延伸，即先检查一度关系，再检查二度关系。顺便问一句：将先检查Claire还是Anuj呢？Claire是一度关系，而Anuj是二度关系，因

此将先检查Claire，后检查Anuj。

 

你也可以这样看，一度关系在二度关系之前加入查找名单。

 

你按顺序依次检查名单中的每个人，看看他是否是芒果销售商。这将先在一度关系中查找，再在二度关系中查找，因此找到的是关系最近的芒果销售商。广度优先搜索不仅查找从A到B的路径，而且找到的是最短的路径。

注意，只有按添加顺序查找时，才能实现这样的目的。换句话说，如果Claire先于Anuj加入名单，就需要先检查Claire，再检查Anuj。如果Claire和Anuj都是芒果销售商，而你先检查Anuj再检查Claire，结果将如何呢？找到的芒果销售商并非是与你关系最近的，因为Anuj是你朋友的朋友，而Claire是你的朋友。因此，你需要按添加顺序进行检查。有一个可实现这种目的的数据

结构，那就是队列（queue）。

 

六、队列

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。

 

队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队，从队列中删除一个队列元素称为出队。因为队列只允许在一端插入，在另一端删除，所以只有最早进入队列的元素才能最先从队列中删除，故队列又称为先进先出（FIFO—first in first out）线性表。

 

顺序队列

建立顺序队列结构必须为其静态分配或动态申请一片连续的存储空间，并设置两个指针进行管理。一个是队头指针front，它指向队头元素；另一个是队尾指针rear，它指向下一个入队元素的存储位置，如图所示

 

 

 

每次在队尾插入一个元素是，rear增1；每次在队头删除一个元素时，front增1。随着插入和删除操作的进行，队列元素的个数不断变化，队列所占的存储空间也在为队列结构所分配的连续空间中移动。当front=rear时，队列中没有任何元素，称为空队列。当rear增加到指向分配的连续空间之外时，队列无法再插入新元素，但这时往往还有大量可用空间未被占用，这些空间是已经出队的队列元素曾经占用过得存储单元。

 

顺序队列中的溢出现象：

 

（1） "下溢"现象：当队列为空时，做出队运算产生的溢出现象。“下溢”是正常现象，常用作程序控制转移的条件。

 

（2）"真上溢"现象：当队列满时，做进栈运算产生空间溢出的现象。“真上溢”是一种出错状态，应设法避免。

 

（3）"假上溢"现象：由于入队和出队操作中，头尾指针只增加不减小，致使被删元素的空间永远无法重新利用。当队列中实际的元素个数远远小于向量空间的规模时，也可能由于尾指针已超越向量空间的上界而不能做入队操作。该现象称为"假上溢"现象。

 

 

循环队列

在实际使用队列时，为了使队列空间能重复使用，往往对队列的使用方法稍加改进：无论插入或删除，一旦rear指针增1或front指针增1 时超出了所分配的队列空间，就让它指向这片连续空间的起始位置。自己真从MaxSize-1增1变到0，可用取余运算rear%MaxSize和front%MaxSize来实现。这实际上是把队列空间想象成一个环形空间，环形空间中的存储单元循环使用，用这种方法管理的队列也就称为循环队列。除了一些简单应用之外，真正实用的队列是循环队列。 [2] 

 

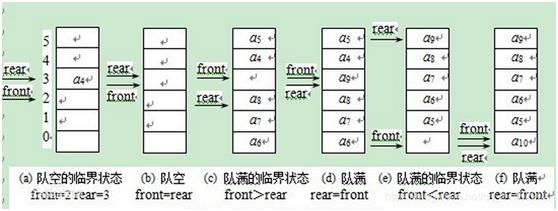
在循环队列中，当队列为空时，有front=rear，而当所有队列空间全占满时，也有front=rear。为了区别这两种情况，规定循环队列最多只能有MaxSize-1个队列元素，当循环队列中只剩下一个空存储单元时，队列就已经满了。因此，队列判空的条件时front=rear，而队列判满的条件时front=（rear+1）%MaxSize。队空和队满的情况如图：

七、广度优先搜索算法实现

我们要从“你”出发找到“ANUJ”，关系表示为下图，使用广度优先搜索算法

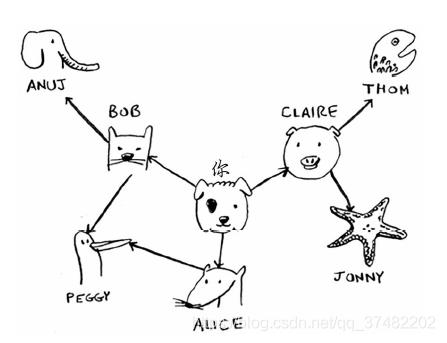
先概述一下这种算法的工作原理。

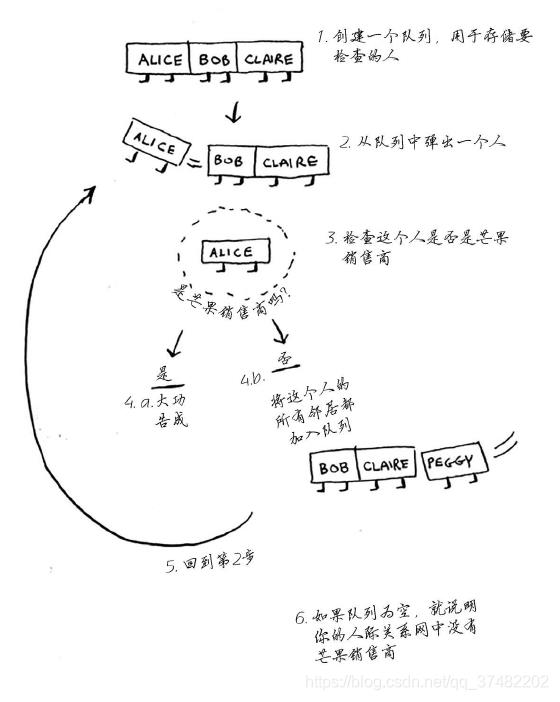
但这样可能会出现一些问题，Peggy既是Alice的朋友又是Bob的朋友，因此她将被加入队列两次：一次是在添加Alice的朋友时，另一次是在添加Bob的朋友时。因此，搜索队列将包含两个Peggy。

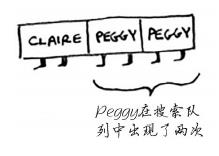
但你只需检查Peggy一次，看她是不是芒果销售商。如果你检查两次，就做了无用功。因此，检查完一个人后，应将其标记为已检查，且不再检查他。如果不这样做，就可能会导致无限循环。假设你的人际关系网类似于下面这样。

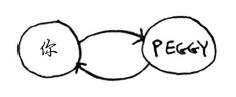
一开始，搜索队列包含你的所有邻居。

现在你检查Peggy。她不是芒果销售商，因此你将其所有邻居都加入搜索队列。

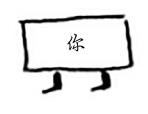
接下来，你检查自己。你不是芒果销售商，因此你将你的所有邻居都加入搜索队列。

以此类推。这将形成无限循环，因为搜索队列将在包含你和包含Peggy之间反复切换。

检查一个人之前，要确认之前没检查过他，这很重要。为此，你可使用一个列表来记录检查过的人。

 

首先，需要使用代码来实现图。图由多个节点组成。

每个节点都与邻近节点相连，如果表示类似于“你→Bob”这样的关系呢？好在你知道的一种结构让你能够表示这种关系，它就是散列表！

记住，散列表让你能够将键映射到值。在这里，你要将节点映射到其所有邻居。

 

图不过是一系列的节点和边

运行时间

如果你在你的整个人际关系网中搜索芒果销售商，就意味着你将沿每条边前行（记住，边是从一个人到另一个人的箭头或连接），因此运行时间至少为O(边数)。

你还使用了一个队列，其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的，即为O(1)，因此对每个人都这样做需要的总时间为O(人数)。所以，广度优先搜索的运行时间为O(人数 + 边数)，这通常写作O(V + E)，其中V为顶点（vertice）数，E为边数。