Codeforces Round #727 (Div. 2)（补题）

Posted 2021-06-29 佐鼬Jun

A. Contest Start

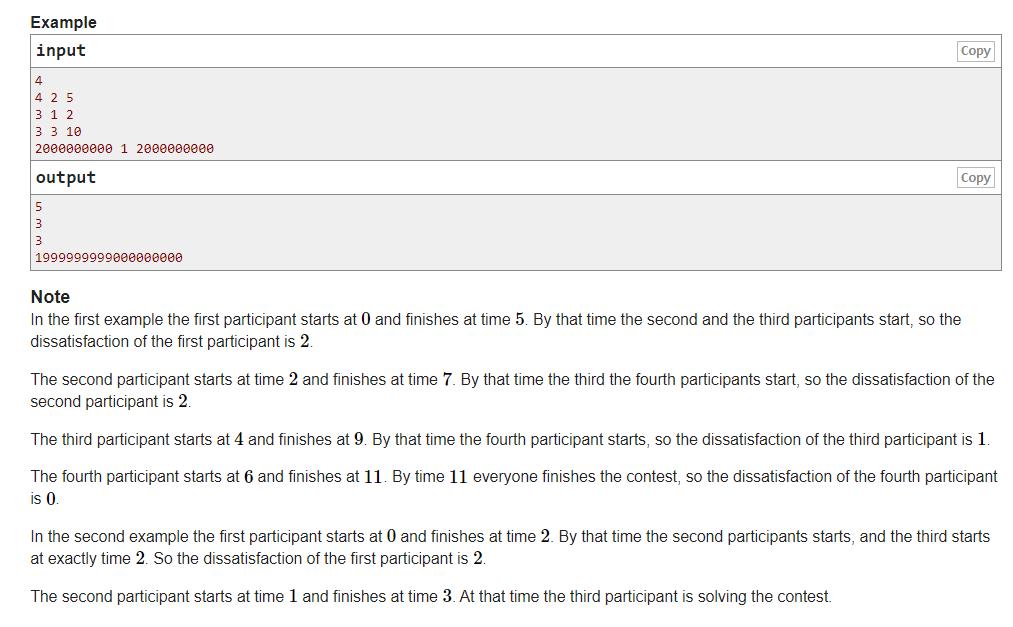
题意： n个人，所以人依次从0,x,2x…开始跑步，每个人都会跑$t$时间，意味着每个人会在t、x+t,2x+t时间点结束跑步。在每个人结束跑步的时候，都要说，还有几个人正在跑步（刚开始跑步也算），最后求和输出。
思路：分2种情况
$1.$第一人结束跑步的时候，剩下所有都开始跑步了，那么每个人都会报数n-1,n-2,n-3…1，直接等差数列求和即可
$2.$第一人结束跑步的时候，还有没开始跑步的。$t/x$就是前面的人跑完后会报的数，而最后不会报这个数的人会是也就是$t/x$个人,前面那些人都会报数$t/x$，$t/x$记为cnt，后面的人报数会是等差数列，cnt-1，cnt-2,…1,所以总和就是$cnt\ast (cnt-1)/2+cnt\ast num$，num就是前面那些数。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
int t;

int main() {
    cin >> t;
    while (t--) {
        ll n, x, t;
        scanf("%lld%lld%lld", &n, &x, &t);
        ll cnt = t / x;
        if (cnt >= n) {
            ll ans = (n) * (n - 1) / 2;
            printf("%lld\\n", ans);
        } else {
            ll num = n - cnt;
            ll ans = cnt * (cnt - 1) / 2 + cnt * num;
            printf("%lld\\n", ans);
        }
    }
    return 0;
}

B. Love Song

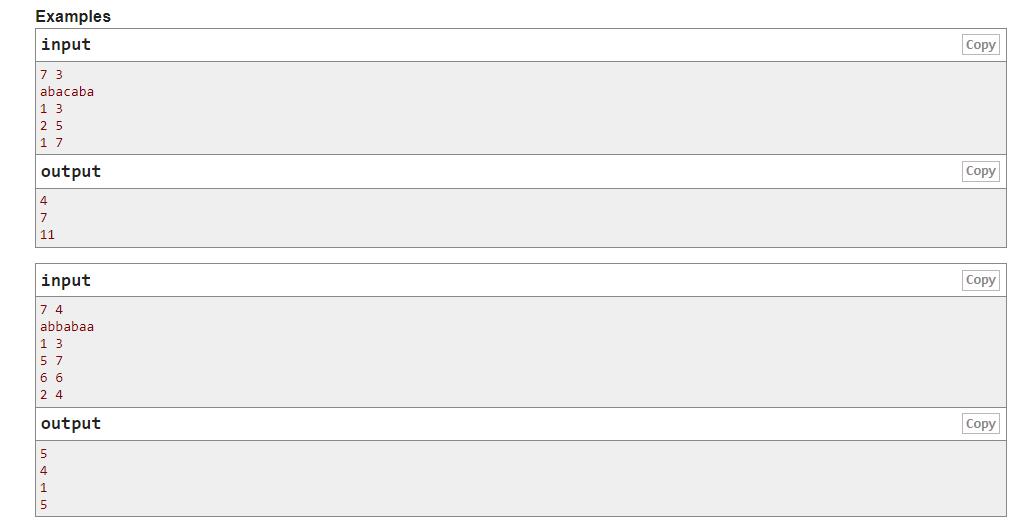
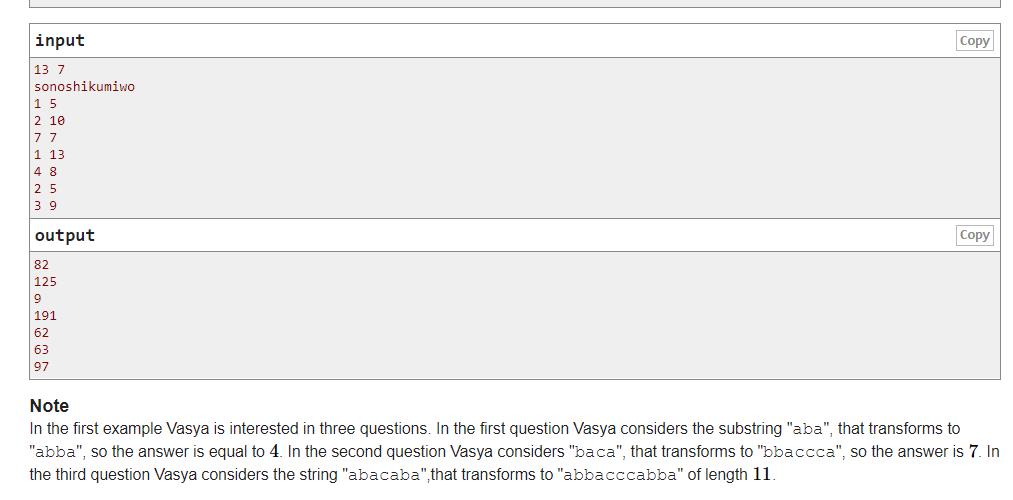
题意： 给一个字符串，每次会选择[L,R]这个区间的子段，里面有a，就会重复1次，有b就会重复2次，…z重复26次。例如abc就会变成,abbccc长度为6. 询问q次，每次输出子段重复完后的字符串长度
思路： 直接前缀和预处理，然后输出需要查询的区间的和，也就是重复后的字符串长度。

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
#define ll long long
char s[N];
ll sum[N];
int main() {
    int n, q;
    scanf("%d%d", &n, &q);
    scanf("%s", s + 1);
    for (int i = 1; i <= n; i++) {
        sum[i] = sum[i - 1] + (s[i] - 'a' + 1);
    }
    while (q--) {
        int l, r;
        scanf("%d%d", &l, &r);
        printf("%lld\\n", sum[r] - sum[l - 1]);
    }
    return 0;
}

C. Stable Groups

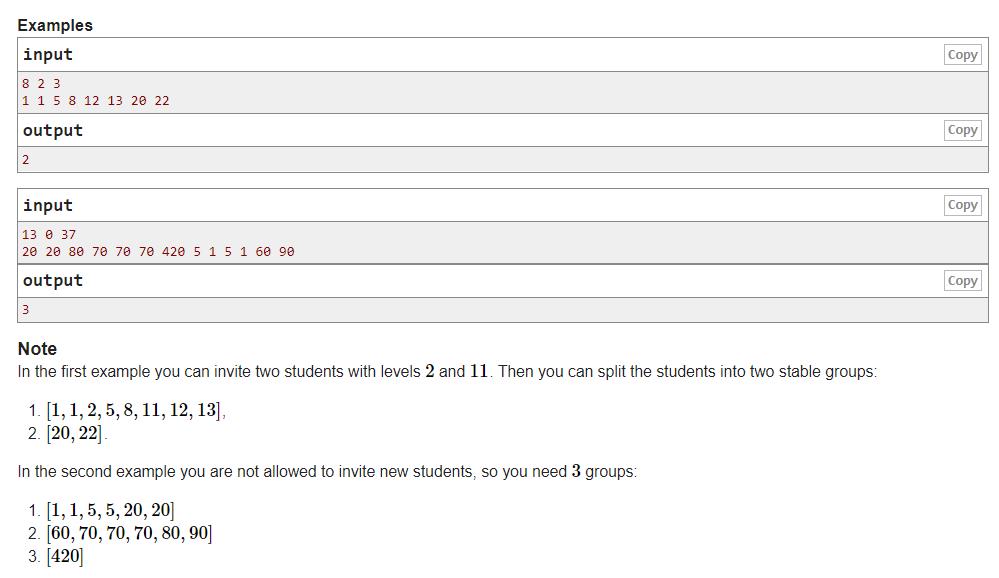
题意： 给n个学生，规定相邻成绩的学生的成绩差不能超过x,只要每个学生都符合，那么这个班就是稳定版，否则就不是。现在可以调用k个任意成绩的学生，问在有n个学生的成绩下，最少可以组成几个稳定班。
思路： 一开始先不添加k个学生，先排序后，把这n个学生组成ans个稳定班，并且记录每个稳定班之间的分数差（分数断层），再排序，往稳定班与稳定班之间添加学生，来使两个稳定班之间融合成一个稳定班。贪心的思想，尽量往分数差之间小的地方来添人。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 200010;
ll n, k, x;
ll a[N];
ll b[N];
int main() {
    cin >> n >> k >> x;
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    sort(a + 1, a + n + 1);
    ll cnt = 0;
    ll ans = 0;
    for (int i = 1; i <= n; i++) {
        int j = i;
        while (j < n && a[j + 1] - a[j] <= x) j++;
        ans++;
        if (i != 1) {
            b[cnt++] = (a[i] - a[i - 1] - 1) / x;
        }
        i = j;
    }
    sort(b, b + cnt);
    for (int i = 0; i < cnt; i++) {
        if (b[i] <= k) {
            ans--;
            k -= b[i];
        }
    }
    printf("%lld\\n", ans);
    return 0;
}

D. PriceFixed

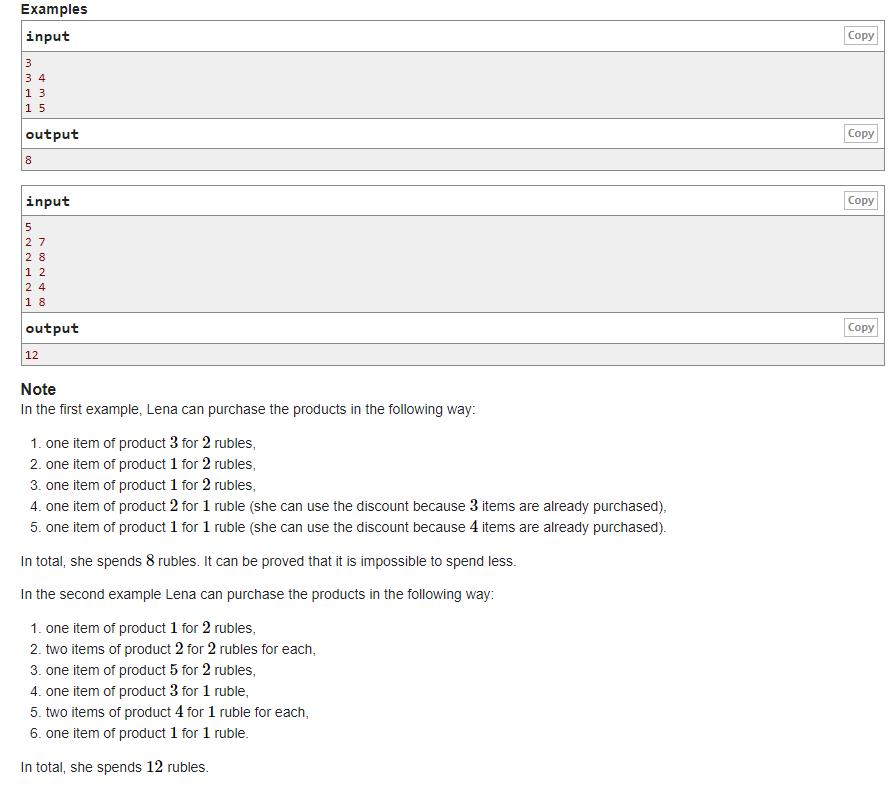
题意： 有n个物品，原价都是2元，第i个物品需要购买$a_i$件，当买$b_i$个物品时这个物品半价（这个是不限买哪个物品数量的）。问购买所需物品数量，最少需要花多少钱。
注意： 为了花钱少，可以买物品比需要的还多以求打折
思路： 双指针思路，对买多少物品才打折$b_i$进行排序，$l=1,r=n$，当前这个物品没到打折要求，那买用r所指的物品来凑，如果凑不够，那就r往右移，接着凑。
之所以要这么做，是因为要求花钱少，就要对那些打折少的进行打折策略，那些打折要求高的要凑出打着要求，反而要花钱数多。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e5+10;
struct node {
    ll a,b;
}s[N];
bool cmp(node i,node j) {
    return i.b<j.b;
}
int main() {
    ll n;
    scanf("%lld",&n);
    for(ll i=1;i<=n;i++) {
        scanf("%lld%lld",&s[i].a,&s[i].b);
    }
    sort(s+1,s+n+1,cmp);
    ll l=1,r=n;
    ll res=0;
    ll cnt=0;
    ll num=0;
    while(l<=r) {
        if(s[l].b<=cnt) {
            cnt+=s[l].a;
            res+=s[l].a;
            l++;
        }
        else {
            num=min(s[r].a,s[l].b-cnt);
            cnt+=num;
            res+=2*num;
            s[r].a-=num;
            if(!s[r].a) r--; 
        }
    }
    printf("%lld\\n",res);
    return 0;
}

To be continued
如果你有任何建议或者批评和补充，请留言指出，不胜感激