人工智能数学基础01--高等数学基础(函数的连续和间断)
Posted 剑威
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了人工智能数学基础01--高等数学基础(函数的连续和间断)相关的知识,希望对你有一定的参考价值。
函数的连续性

函数在一点处连续:设 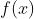 在
在 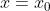 的某邻域
的某邻域 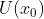 有定义,且
有定义,且 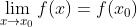 。则称
。则称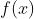 在
在 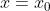 处连续。换句话说,如果当自变量的改变量
处连续。换句话说,如果当自变量的改变量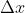 趋近于零时,相应的函数值的改变量
趋近于零时,相应的函数值的改变量 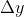 也趋近于零,则称
也趋近于零,则称 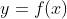 在点
在点 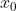 处连续。
处连续。
函数在一点处左连续:设 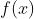 在
在 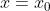 的左侧某邻域
的左侧某邻域  有定义,且
有定义,且 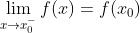 ,则称
,则称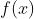 在
在 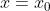 处左连续,类似地可以定义右连续。
处左连续,类似地可以定义右连续。
函数在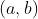 内,
内,![\\left [ a,b \\right ]](https://image.cha138.com/20210628/c533358904bb46cf9858d4d80eb48ccf.jpg) 上连续:设
上连续:设 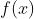 在
在 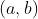 内每一点处都连续,则称
内每一点处都连续,则称 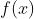 在
在 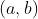 内连续。定义
内连续。定义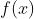 在
在 ![[a,b]](https://image.cha138.com/20210628/736fd6a17ca3451b8fb62abe475318bf.jpg) 上连续,其中在
上连续,其中在  处指的是右连续,
处指的是右连续,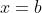 处指的是左连续。
处指的是左连续。
函数的间断点
第一类间断点:设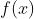 在
在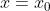 的某去心邻域内有定义,如果
的某去心邻域内有定义,如果 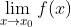 存在,但
存在,但 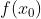
无定义,或者虽然有定义,但与 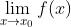 不相等,称
不相等,称 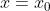 为
为 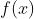 的可去间断点。
的可去间断点。
设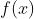 在
在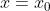 的某去心邻域内有定义,如果
的某去心邻域内有定义,如果 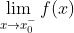 与
与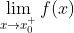 都存在,但不相等,称
都存在,但不相等,称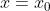 为
为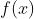 的跳跃间断点。此时不论
的跳跃间断点。此时不论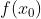 是否存在,存在时等于什么都无关。
是否存在,存在时等于什么都无关。
可去间断点和跳跃间断点统称为第一类间断点。
第二类间断点:
设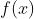 在
在 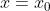 的某去心邻域内有定义,如果
的某去心邻域内有定义,如果 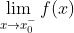 与
与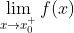 至少有一个不存在,称
至少有一个不存在,称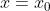 为
为 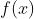 的第二类间断点,第二类间断点又可细分为无穷间断点,振荡间断点等。
的第二类间断点,第二类间断点又可细分为无穷间断点,振荡间断点等。
例如: 在
在 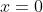 处为无穷间断点;
处为无穷间断点;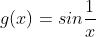 在
在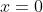 处为振荡间断点。
处为振荡间断点。
重要性质、定理、公式
连续函数的四则运算:设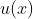 与
与 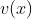 在
在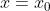 处连续,则四则运算之后所成的函数在
处连续,则四则运算之后所成的函数在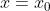 处也连续(除法运算时要求分母不为零)。
处也连续(除法运算时要求分母不为零)。
复合函数的连续性:设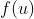 在
在 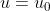 处连续,
处连续,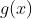 在
在 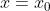 处连续,且
处连续,且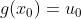 ,则复合函数
,则复合函数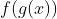 在
在 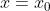 处亦连续。
处亦连续。
基本初等函数的连续性:基本初等函数在它的定义域上都是连续的。
初等函数的连续性:初等函数正它的定义域的区间内都是连续的。
闭区间上的连续函数的性质:设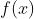 在闭区间
在闭区间![\\left [ a,b \\right ]](https://image.cha138.com/20210628/c533358904bb46cf9858d4d80eb48ccf.jpg) 上连续,则它具有下列性质:
上连续,则它具有下列性质:
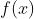 在
在![\\left [ a,b \\right ]](https://image.cha138.com/20210628/c533358904bb46cf9858d4d80eb48ccf.jpg) 上有界(称为有界性定理);
上有界(称为有界性定理);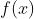 在
在![\\left [ a,b \\right ]](https://image.cha138.com/20210628/c533358904bb46cf9858d4d80eb48ccf.jpg) 上有最大值与最小值(称为最值定理);
上有最大值与最小值(称为最值定理);- 设
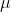 满足
满足 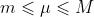 ,
, 和
和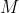 分别为
分别为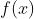 在
在![\\left [ a,b \\right ]](https://image.cha138.com/20210628/c533358904bb46cf9858d4d80eb48ccf.jpg) 上的最小值与最大值,则至少存在一点
上的最小值与最大值,则至少存在一点![\\xi \\in \\left [ a,b \\right ]](https://image.cha138.com/20210628/5b20bb88d37843da855f44581cdf7531.jpg) ,使
,使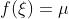 (称为介值定理);(若
(称为介值定理);(若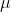 满足
满足 ,则
,则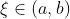 。)
。) - 设
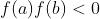 ,则至少存在一点
,则至少存在一点 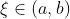 ,使
,使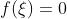 (称为零点定理)。
(称为零点定理)。
以上是关于人工智能数学基础01--高等数学基础(函数的连续和间断)的主要内容,如果未能解决你的问题,请参考以下文章