Pytorch Note18 优化算法4 RMSprop算法
Posted Real&Love
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Pytorch Note18 优化算法4 RMSprop算法相关的知识,希望对你有一定的参考价值。
Pytorch Note18 优化算法4 RMSprop算法
全部笔记的汇总贴:Pytorch Note 快乐星球
RMSprop
RMSprop 是由 Geoff Hinton 在他 Coursera 课程中提出的一种适应性学习率方法,至今仍未被公开发表。前面我们提到了 Adagrad 算法有一个问题,就是学习率分母上的变量 s 不断被累加增大,最后会导致学习率除以一个比较大的数之后变得非常小,这不利于我们找到最后的最优解,所以 RMSProp 的提出就是为了解决这个问题。
RMSProp 算法
RMSProp 仍然会使用梯度的平方量,不同于 Adagrad,RMSProp算法将这些梯度按元素平⽅做指数加权移动平均。具体来说,给定超参数0 ≤ γ < 1,RMSProp算法在时间步t > 0计算:
s
i
=
γ
s
i
−
1
+
(
1
−
γ
)
g
2
s_i = \\gamma s_{i-1} + (1 - \\gamma) \\ g^2
si=γsi−1+(1−γ) g2
这里 g 表示当前求出的参数梯度,然后最终更新和 Adagrad 是一样的,学习率变成了
η s + ϵ \\frac{\\eta}{\\sqrt{s + \\epsilon}} s+ϵη
这里 α \\alpha α 是一个移动平均的系数,也是因为这个系数,导致了 RMSProp 和 Adagrad 不同的地方,这个系数使得 RMSProp 更新到后期累加的梯度平方较小,从而保证 s 不会太大,⾃变量每个元素的学习率在迭代过程中就不再⼀直降低,也就使得模型后期依然能够找到比较优的结果。
简单来说,使用的是指数加权平均,旨在消除梯度下降中的摆动,与Momentum的效果一样,某一维度的导数比较大,则指数加权平均就大,某一维度的导数比较小,则其指数加权平均就小,这样就保证了各维度导数都在一个量级,进而减少了摆动。允许使用一个更大的学习率η
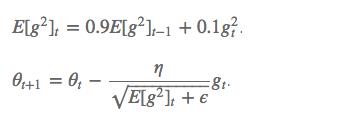
Hinton 建议设定γ为 0.9, 学习率 η 为 0.001。
代码从0实现
我们还是利用minst的数据
import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline
def data_tf(x):
x = np.array(x, dtype='float32') / 255
x = (x - 0.5) / 0.5 # 标准化,这个技巧之后会讲到
x = x.reshape((-1,)) # 拉平
x = torch.from_numpy(x)
return x
train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集,申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)
# 定义 loss 函数
criterion = nn.CrossEntropyLoss()
def rmsprop(parameters, sqrs, lr, alpha):
eps = 1e-10
for param, sqr in zip(parameters, sqrs):
sqr[:] = alpha * sqr + (1 - alpha) * param.grad.data ** 2
div = lr / torch.sqrt(sqr + eps) * param.grad.data
param.data = param.data - div
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
# 初始化梯度平方项
sqrs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
# 开始训练
losses = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.9) # 学习率设为 0.001,alpha 设为 0.9
# 记录误差
train_loss += loss.data
if idx % 30 == 0:
losses.append(loss.data)
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
epoch: 0, Train Loss: 0.381906 epoch: 1, Train Loss: 0.174923 epoch: 2, Train Loss: 0.128508 epoch: 3, Train Loss: 0.104501 epoch: 4, Train Loss: 0.091484 使用时间: 35.81994 s
x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='alpha=0.9')
plt.legend(loc='best')
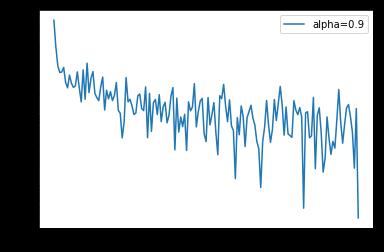
我们调整一下我们alpha的值
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
# 初始化梯度平方项
sqrs = []
for param in net.parameters():
sqrs.append(torch.zeros_like(param.data))
# 开始训练
losses = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
net.zero_grad()
loss.backward()
rmsprop(net.parameters(), sqrs, 1e-3, 0.999) # 学习率设为 0.001,alpha 设为 0.999
# 记录误差
train_loss += loss.data[0]
if idx % 30 == 0:
losses.append(loss.data[0])
idx += 1
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
epoch: 0, Train Loss: 0.482363 epoch: 1, Train Loss: 0.169266 epoch: 2, Train Loss: 0.132606 epoch: 3, Train Loss: 0.111919 epoch: 4, Train Loss: 0.096000 使用时间: 32.14718 s
x_axis = np.linspace(0, 5, len(losses), endpoint=True)
plt.semilogy(x_axis, losses, label='alpha=0.999')
plt.legend(loc='best')
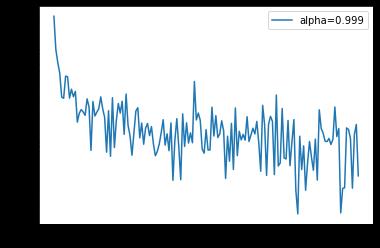
可以看到使用了不同的 alpha 会使得 loss 在下降过程中的震荡程度不同
pytorch内置优化器
当然 pytorch 也内置了 rmsprop 的方法,非常简单,只需要调用 torch.optim.RMSprop() 就可以了,下面是例子
train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
nn.Linear(784, 200),
nn.ReLU(),
nn.Linear(200, 10),
)
optimizer = torch.optim.RMSprop(net.parameters(), lr=1e-3, alpha=0.9)
# 开始训练
start = time.time() # 记时开始
for e in range(5):
train_loss = 0
for im, label in train_data:
im = Variable(im)
label = Variable(label)
# 前向传播
out = net(im)
loss = criterion(out, label)
# 反向传播
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 记录误差
train_loss += loss.data[0]
print('epoch: {}, Train Loss: {:.6f}'
.format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))
epoch: 0, Train Loss: 0.378526 epoch: 1, Train Loss: 0.167142 epoch: 2, Train Loss: 0.124586 epoch: 3, Train Loss: 0.102094 epoch: 4, Train Loss: 0.088567 使用时间: 37.01984 s
可视化
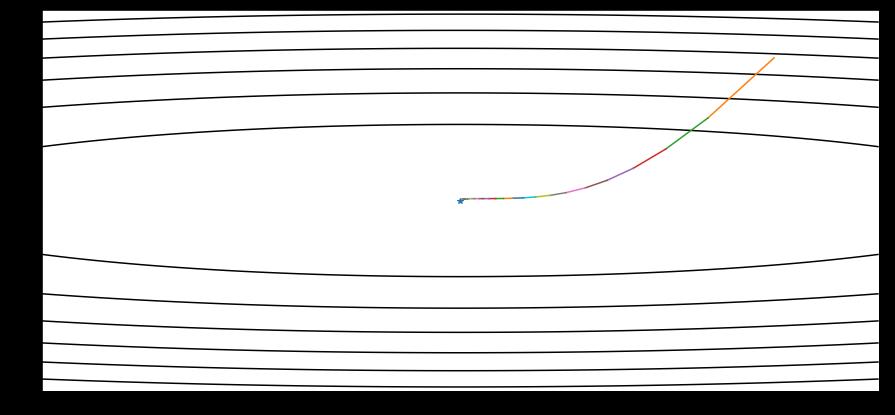
以上是关于Pytorch Note18 优化算法4 RMSprop算法的主要内容,如果未能解决你的问题,请参考以下文章
Pytorch Note16 优化算法2 动量法(Momentum)
Pytorch Note15 优化算法1 梯度下降(Gradient descent varients)