Pytorch Note15 优化算法1 梯度下降（Gradient descent varients）

Posted 2021-06-27 Real&Love

Pytorch Note15 优化算法1 梯度下降（Gradient descent varients）

文章目录

• Pytorch Note15 优化算法1 梯度下降（Gradient descent varients）
• • 优化算法1 梯度下降（Gradient descent varients）
  • 1.Batch Gradient Descent （BGD）
  • 2.Stochastic Gradient Descent（SGD）
  • 3.Mini-batch Gradient Descent（MBGD）
  • Challenge挑战
  • 从0开始代码实现
  • • SGD
    • BGD
    • MBGD batch_size = 64
    • 调高学习率
  • pytorch内置优化器
  • 可视化

全部笔记的汇总贴： Pytorch Note 快乐星球

优化算法1 梯度下降（Gradient descent varients）

梯度下降有三种变形，主要的不同就是在于我们使用多少数据来计算我们的目标函数的梯度。我们可以根据我们的数据量，去 trade off 我们的参数更新的准确率和运行时间。

1.Batch Gradient Descent （BGD）

批量梯度下降（BGD），会采用整个训练集的数据来计算cost function 对参数的梯度：

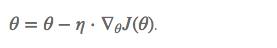
由于我们需要计算整个数据集的梯度以仅执行一次更新，因此批量梯度下降可能非常慢，并且对于数据很大的数据集来说是难以处理的。 批量梯度下降也不允许我们实时更新我们的模型，即投入新数据实时更新模型。

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

首先我们会预先定义一个迭代次数epoch，然后计算我们的梯度向量 params_grad，接着我们会沿着梯度方向去更行我们的参数params，learning_rate 是我们的学习率，相当于是步长，这会决定我们每一步会迈多大。

对于凸函数来说，BGD可以保证收敛到全局最小值 global minimum，但是对于非凸函数可以收敛到局部最小值 local minimum

2.Stochastic Gradient Descent（SGD）

随机梯度下降（SGD）与BGD相比，随机梯度下降 (SGD) 对每个训练示例 x (i) 和标签 y (i) 执行参数更新:

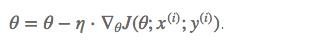
对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，因为它在每次更新参数之前重新计算相似示例的梯度。 SGD 通过一次执行一次更新来消除这种冗余。 因此，它通常要快得多，也可用于在线学习，可以新增样本。 SGD 以高方差执行频繁更新，导致目标函数大幅波动。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

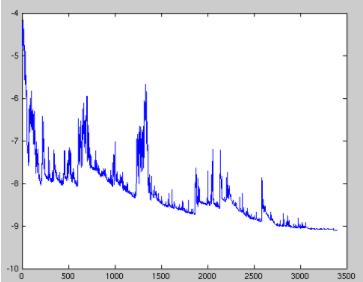
随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况，那么可能只用其中部分的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。缺点是SGD的噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。所以虽然训练速度快，但是准确度下降，并不是全局最优。虽然包含一定的随机性，但是从期望上来看，它是等于正确的导数的。

缺点：

SGD 因为更新比较频繁，会造成 cost function 有严重的震荡。

BGD 可以收敛到局部极小值，当然 SGD 的震荡可能会跳到更好的局部极小值处。

当我们稍微减小 learning rate，SGD 和 BGD 的收敛性是一样的。

3.Mini-batch Gradient Descent（MBGD）

小批量梯度下降（MBGD）最终采用了两全其美的方法，并对每个小批量的 n 个训练示例执行更新：

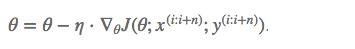
和 SGD 的区别是每一次循环不是作用于每个样本，而是具有 n 个样本的批次

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

这样，它 a) 减少了参数更新的方差，这可以导致更稳定的收敛； b) 可以利用最先进的深度学习库常见的高度优化的矩阵优化来计算梯度。小批量非常有效。 常见的小批量大小范围在 50 到 256 之间，但可能因不同的应用程序而异。 小批量梯度下降通常是训练神经网络时选择的算法，并且在使用小批量时通常也会使用术语 SGD。

Challenge挑战

然而，其实mini-batch 梯度下降并不能保证良好的收敛性，还是存在一些挑战：

• learning rate 如果选择的太小，收敛速度会很慢，如果太大，loss function 就会在极小值处不停地震荡甚至偏离。
• 有一种Learning rate schedules学习措施尝试在训练期间调整学习率，例如： 退火，即根据预定义的时间或当 epoch 之间的目标变化低于阈值时降低学习率。比如当两次迭代之间的变化低于某个阈值后，就减小 learning rate，不过这个阈值的设定需要提前写好，这样的话就不能够适应数据集的特点。
• 此外，相同的学习率适用于所有参数更新。 如果我们的数据是稀疏的并且我们的特征具有非常不同的频率，我们可能不想将它们全部更新到相同的程度，而是对很少出现的特征执行更大的更新。我们更希望对出现频率低的特征进行大一点的更新。LR会随着更新的次数逐渐变小。
• 对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的error是一样的，所有维度的梯度都接近于0，SGD 很容易被困在这里。（会在鞍点或者局部最小点震荡跳动，因为在此点处，如果是训练集全集带入即BGD，则优化会停止不动，如果是mini-batch或者SGD，每次找到的梯度都是不同的，就会发生震荡，来回跳动。）

鞍点就是：一个光滑函数的鞍点邻域的曲线，曲面，或超曲面，都位于这点的切线的不同边。例如这个二维图形，像个马鞍：在x-轴方向往上曲，在y-轴方向往下曲，鞍点就是（0，0）。

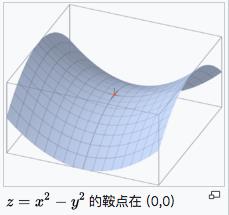
从0开始代码实现

前面我们介绍了梯度下降法的数学原理，下面我们通过例子来说明一下随机梯度下降法，我们分别从 0 自己实现，以及使用 pytorch 中自带的优化器

我们会调节我们的超参数batch_size

• batch_size=1，就是SGD。
• batch_size=n，就是mini-batch
• batch_size=m，就是batch

其中1<n<m，m表示整个训练集大小。

一般的 mini-batch 大小为 32 到 512，考虑到电脑内存设置和使用的方式，如果 mini-batch 大小是 2 的𝑛次方，代码会运行地快一些。

我们会用torchvision内置的mnist数据

import numpy as np
import torch
from torchvision.datasets import MNIST # 导入 pytorch 内置的 mnist 数据
from torch.utils.data import DataLoader
from torch import nn
from torch.autograd import Variable
import time
import matplotlib.pyplot as plt
%matplotlib inline

def data_tf(x):
    x = np.array(x, dtype='float32') / 255 # 将数据变到 0 ~ 1 之间
    x = (x - 0.5) / 0.5 # 标准化，这个技巧之后会讲到
    x = x.reshape((-1,)) # 拉平
    x = torch.from_numpy(x)
    return x

train_set = MNIST('./data', train=True, transform=data_tf, download=True) # 载入数据集，申明定义的数据变换
test_set = MNIST('./data', train=False, transform=data_tf, download=True)

# 定义 loss 函数
criterion = nn.CrossEntropyLoss()

SGD

随机梯度下降法非常简单，公式就是
$${\theta }_{i+1}={\theta }_i-\eta \nabla L(\theta )$$
非常简单，我们可以从 0 开始自己实现

def sgd_update(parameters, lr):
    for param in parameters:
        param.data = param.data - lr * param.grad.data

我们可以将 batch size 先设置为 1，看看有什么效果

train_data = DataLoader(train_set, batch_size=1, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

# 开始训练
losses1 = []
idx = 0

start = time.time() # 记时开始
for e in range(5):
    train_loss = 0
    for im, label in train_data:
        im = Variable(im)
        label = Variable(label)
        # 前向传播
        out = net(im)
        loss = criterion(out, label)
        # 反向传播
        net.zero_grad()
        loss.backward()
        sgd_update(net.parameters(), 1e-2) # 使用 0.01 的学习率
        # 记录误差
        train_loss += loss.data[0]
        if idx % 30 == 0:
            losses1.append(loss.data[0])
        idx += 1
    print('epoch: {}, Train Loss: {:.6f}'
          .format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

epoch: 0, Train Loss: 0.350992
epoch: 1, Train Loss: 0.215084
epoch: 2, Train Loss: 0.180627
epoch: 3, Train Loss: 0.159482
epoch: 4, Train Loss: 0.143023
使用时间: 315.65429 s

x_axis = np.linspace(0, 5, len(losses1), endpoint=True)
plt.semilogy(x_axis, losses1, label='batch_size=1')
plt.legend(loc='best')

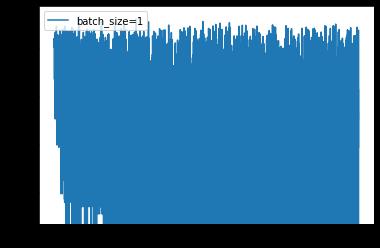
可以看到，loss 在剧烈震荡，因为每次都是只对一个样本点做计算，每一层的梯度都具有很高的随机性，而且需要耗费了大量的时间

BGD

train_data = DataLoader(train_set, batch_size=len(train_set), shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

# 开始训练
losses4 = []
idx = 0

start = time.time() # 记时开始
for e in range(50):
    train_loss = 0
    for im, label in train_data:
        im = Variable(im)
        label = Variable(label)
        # 前向传播
        out = net(im)
        loss = criterion(out, label)
        # 反向传播
        net.zero_grad()
        loss.backward()
        sgd_update(net.parameters(), 1e-2) # 使用 0.01 的学习率
        # 记录误差
        train_loss += loss.data
#         if idx % 30 == 0:
        losses4.append(loss.data)
        idx += 1
    print('epoch: {}, Train Loss: {:.6f}'
          .format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

x_axis = np.linspace(0, 5, len(losses4), endpoint=True)
plt.semilogy(x_axis, losses4, label='batch_size = 60000')
plt.legend(loc='best')

可以看得出来，如果BGD会慢慢下降，但是可能在相同的学习率的时候会慢一些

MBGD batch_size = 64

train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

# 开始训练
losses2 = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
    train_loss = 0
    for im, label in train_data:
        im = Variable(im)
        label = Variable(label)
        # 前向传播
        out = net(im)
        loss = criterion(out, label)
        # 反向传播
        net.zero_grad()
        loss.backward()
        sgd_update(net.parameters(), 1e-2)
        # 记录误差
        train_loss += loss.data
        if idx % 30 == 0:
            losses2.append(loss.data)
        idx += 1
    print('epoch: {}, Train Loss: {:.6f}'
          .format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

epoch: 0, Train Loss: 0.747719
epoch: 1, Train Loss: 0.366298
epoch: 2, Train Loss: 0.320198
epoch: 3, Train Loss: 0.292184
epoch: 4, Train Loss: 0.269337
使用时间: 39.34448 s

x_axis = np.linspace(0, 5, len(losses2), endpoint=True)
plt.semilogy(x_axis, losses2, label='batch_size=64')
plt.legend(loc='best')

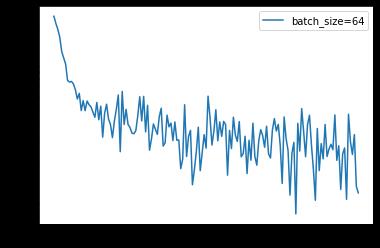
通过上面的结果可以看到 loss 没有 batch 等于 1 震荡那么距离，同时也可以降到一定的程度了，时间上也比之前快了非常多，因为按照 batch 的数据量计算上更快，同时梯度对比于 batch size = 1 的情况也跟接近真实的梯度，所以 batch size 的值越大，梯度也就越稳定，而 batch size 越小，梯度具有越高的随机性，这里 batch size 为 64，可以看到 loss 仍然存在震荡，但这并没有关系，如果 batch size 太大，对于内存的需求就更高，同时也不利于网络跳出局部极小点，所以现在普遍使用基于 batch 的随机梯度下降法，而 batch 的多少基于实际情况进行考虑

调高学习率

train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

# 开始训练
losses3 = []
idx = 0
start = time.time() # 记时开始
for e in range(5):
    train_loss = 0
    for im, label in train_data:
        im = Variable(im)
        label = Variable(label)
        # 前向传播
        out = net(im)
        loss = criterion(out, label)
        # 反向传播
        net.zero_grad()
        loss.backward()
        sgd_update(net.parameters(), 1) # 使用 1.0 的学习率
        # 记录误差
        train_loss += loss.data
        if idx % 30 == 0:
            losses3.append(loss.data)
        idx += 1
    print('epoch: {}, Train Loss: {:.6f}'
          .format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

epoch: 0, Train Loss: 2.480193
epoch: 1, Train Loss: 2.305190
epoch: 2, Train Loss: 2.304795
epoch: 3, Train Loss: 2.304833
epoch: 4, Train Loss: 2.304679
使用时间: 37.32199 s

x_axis = np.linspace(0, 5, len(losses3), endpoint=True)
plt.semilogy(x_axis, losses3, label='lr = 1')
plt.legend(loc='best')

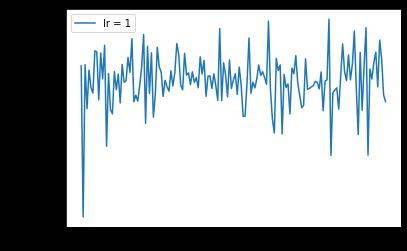
可以看到，学习率太大会使得损失函数不断回跳，从而无法让损失函数较好降低，所以我们一般都是用一个比较小的学习率

pytorch内置优化器

train_data = DataLoader(train_set, batch_size=64, shuffle=True)
# 使用 Sequential 定义 3 层神经网络
net = nn.Sequential(
    nn.Linear(784, 200),
    nn.ReLU(),
    nn.Linear(200, 10),
)

optimzier = torch.optim.SGD(net.parameters(), 1e-2)
# 开始训练

start = time.time() # 记时开始
for e in range(5):
    train_loss = 0
    for im, label in train_data:
        im = Variable(im)
        label = Variable(label)
        # 前向传播
        out = net(im)
        loss = criterion(out, label)
        # 反向传播
        optimzier.zero_grad()
        loss.backward()
        optimzier.step()
        # 记录误差
        train_loss += loss.data
    print('epoch: {}, Train Loss: {:.6f}'
          .format(e, train_loss / len(train_data)))
end = time.time() # 计时结束
print('使用时间: {:.5f} s'.format(end - start))

epoch: 0, Train Loss: 0.747158
epoch: 1, Train Loss: 0.364107
epoch: 2, Train Loss: 0.318209
epoch: 3, Train Loss: 0.290282
epoch: 4, Train Loss: 0.268150
使用时间: 46.75882 s

可视化

就拿函数$f(x)=x^2-2x+1$来当例子，我们用梯度下降法来求最小值

def f(x):
    return x * x - 2 * x + 1

def g(x):
    return 2 * x - 2

def path_show(x,y,arr):
    plt.plot(0,0,marker='*')
    plt.plot(x, y)
    if arr is not None:
        arr = np.array(arr)
        for i in range(len(arr) - 1):
            plt.plot(arr[i:i+2,0],arr[i:i+2,1])

def gd(x_start, step, g):   # gd代表了Gradient Descent
    x = np.array(x_start, dtype='float64')
#     plt.scatter(x,f(x),'*')
    passing_dot = [np.array([x.copy(),f(x)])]
    for i in range(10):
        grad = g(x)
        x -= grad * step
        passing_dot.append(npPytorch Note9 线性模型和梯度下降

 Pytorch中常见的优化算法介绍
 PyTorch深度学习-03梯度下降（快速入门）
 pytorch常用优化器总结(包括warmup介绍及代码实现)
 pytorch常用优化器总结(包括warmup介绍及代码实现)
 pytorch常用优化器总结(包括warmup介绍及代码实现)