Pytorch Note9 线性模型和梯度下降

Posted 2021-06-27 Real&Love

Pytorch Note9 线性模型和梯度下降

• • 一元线性回归
  • 梯度下降法
  • • 梯度
    • 梯度下降法
  • 一维线性模型
  • 建立模型
  • GPU加速
  • 训练模型
  • 训练预测结果

全部笔记的汇总贴：Pytorch Note 快乐星球

一元线性回归

说起线性模型，大家对它都很熟悉了，通俗来讲就是给定很多个数据点，希望能够找到一个函数来拟合这些数据点使其误差最小，比如最简单的一元线性模型

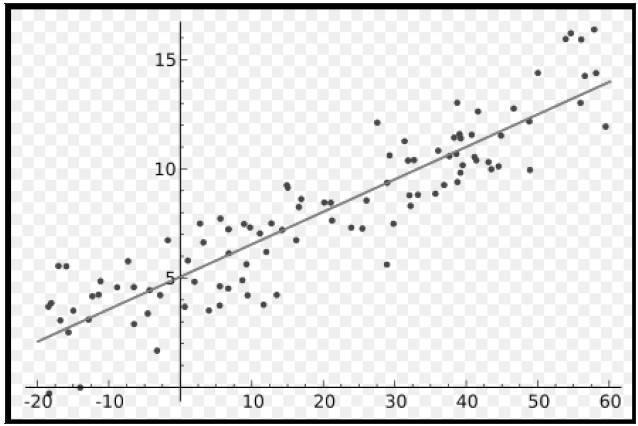
一元线性模型非常简单，假设我们有变量 $x_i$ 和目标 $y_i$，每个 i 对应于一个数据点，希望建立一个模型

$${\hat{y}}_i=w{x}_i+b$$

${\hat{y}}_i$ 是我们预测的结果，希望通过 ${\hat{y}}_i$ 来拟合目标 $y_i$，通俗来讲就是找到这个函数拟合 $y_i$ 使得误差最小，即最小化

$$\frac{1}{n}\sum _{i=1}^n({\hat{y}}_i-y_i{)}^2$$

那么如何最小化这个误差呢？

这里需要用到梯度下降，这是我们接触到的第一个优化算法，非常简单，但是却非常强大，在深度学习中被大量使用，所以让我们从简单的例子出发了解梯度下降法的原理

梯度下降法

在梯度下降法中，我们首先要明确梯度的概念，随后我们再了解如何使用梯度进行下降。

梯度

梯度在数学上就是导数，如果是一个多元函数，那么梯度就是偏导数。比如一个函数f(x, y)，那么 f 的梯度就是

$$(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$

可以称为 grad f(x, y) 或者 $\nabla f(x,y)$。具体某一点 $(x_0,y_0)$ 的梯度就是 $\nabla f(x_0,y_0)$。

梯度有什么意义呢？从几何意义来讲，一个点的梯度值是这个函数变化最快的地方，具体来说，对于函数 f(x, y)，在点 $(x_0,y_0)$ 处，沿着梯度 $\nabla f(x_0,y_0)$ 的方向，函数增加最快，也就是说沿着梯度的方向，我们能够更快地找到函数的极大值点，或者反过来沿着梯度的反方向，我们能够更快地找到函数的最小值点。

梯度下降法

有了对梯度的理解，我们就能了解梯度下降发的原理了。上面我们需要最小化这个误差，也就是需要找到这个误差的最小值点，那么沿着梯度的反方向我们就能够找到这个最小值点。

我们可以来看一个直观的解释。比如我们在一座大山上的某处位置，由于我们不知道怎么下山，于是决定走一步算一步，也就是在每走到一个位置的时候，求解当前位置的梯度，沿着梯度的负方向，也就是当前最陡峭的位置向下走一步，然后继续求解当前位置梯度，向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去，一直走到觉得我们已经到了山脚。当然这样走下去，有可能我们不能走到山脚，而是到了某一个局部的山峰低处。

类比我们的问题，就是沿着梯度的反方向，我们不断改变 w 和 b 的值，最终找到一组最好的 w 和 b 使得误差最小。

在更新的时候，我们需要决定每次更新的幅度，比如在下山的例子中，我们需要每次往下走的那一步的长度，这个长度称为学习率，用 $\eta$ 表示，这个学习率非常重要，不同的学习率都会导致不同的结果，学习率太小会导致下降非常缓慢，学习率太大又会导致跳动非常明显。

最后我们的更新公式就是

$$\begin{gathered} w:=w-\eta \frac{\partial f(w,b)}{\partial w} \\ b:=b-\eta \frac{\partial f(w,b)}{\partial b} \end{gathered}$$

通过不断地迭代更新，最终我们能够找到一组最优的 w 和 b，这就是梯度下降法的原理。

上面是原理部分，下面通过一个例子来进一步学习线性模型

一维线性模型

# 读入数据 x 和 y
x_train = np.array([[3.3], [4.4], [5.5], [6.71], [6.93], [4.168],
                    [9.779], [6.182], [7.59], [2.167], [7.042],
                    [10.791], [5.313], [7.997], [3.1]], dtype=np.float32)

y_train = np.array([[1.7], [2.76], [2.09], [3.19], [1.694], [1.573],
                    [3.366], [2.596], [2.53], [1.221], [2.827],
                    [3.465], [1.65], [2.904], [1.3]], dtype=np.float32)

我们想要做的事情就是找一条直线去逼近这些点，也就是希望这条直线离这些点的距离之和最小，先将numpy.array转换成Tensor，因为pytorch里面的处理单元都是Tensor

x_train = torch.from_numpy(x_train)
y_train = torch.from_numpy(y_train)

画出相应的图像

# 画出图像
import matplotlib.pyplot as plt
%matplotlib inline

plt.plot(x_train, y_train, 'bo')

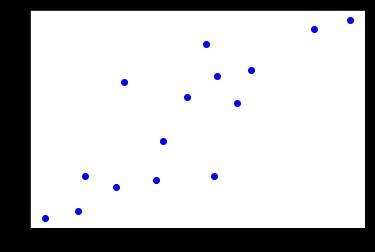
建立模型

接着需要建立我们的模型，这里建立了一个简单的模型

class LinearRegression(nn.Module):
    def __init__(self):
        super(LinearRegression, self).__init__()
        self.linear = nn.Linear(1,1) # 我们的输入和输出都是1维的
        
    def forward(self,x):
        out = self.linear(x)
        return out

这里我们就定义了一个超级简单的模型$y=wx+b$，输入的参数是一维，输出的参数也是一维，这就是一条直线

GPU加速

判断是否能用GPU加速

if torch.cuda.is_available():
    model = LinearRegression().cuda()
else:
    model = LinearRegression()

然后定义损失函数和优化方法，这里使用均方误差作为我们的优化函数，使用随机梯度下降进行优化

criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr = 1e-3)

训练模型

接着就可以开始我们的训练模型

num_epochs = 1000
for epoch in range(num_epochs):
    if torch.cuda.is_available():
        inputs = Variable(x_train).cuda()
        target = Variable(y_train).cuda()
    else:
        inputs = Variable(x_train)
        target = Variable(y_train)
        
    out = model(inputs)
    loss = criterion(out,target)
    
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    if (epoch+1) % 20 == 0:
        print('Epoch[{}:{}], loss: {:.6f}'
             .format(epoch+1,num_epochs,loss.data))

定义好我们要跑的 epoch 个数，然后将数据变成 Variable 放入计算图，然后通过 out=model(inputs) 得到网络前向传播得到的结果，通过 loss=criterion(out,target)得到损失函数，然后归零梯度，做反向传播和更新参数，特别要注意的是，每次做反向传播之前都要归零梯度，optimizer.zero_grad()。不然梯度会累加在一起，造成结果不收敛。在训练的过程中隔一段时间就将损失函数的值打印出来看看，确保我们的模型误差越来越小。注意 loss.data，首先 loss 是一个 Variable，所以通过loss.data可以取出一个 Tensor，再通过loss.data得到一个 int 或者 float 类型的数据，这样我们才能够打印出相应的数据。

训练预测结果

做完训练可以预测我们的结果

model.eval()
predict = model(Variable(x_train).cuda())
predict = predict.data.cpu().numpy()
plt.plot(x_train.numpy(),y_train.numpy(), 'ro', label = 'Original data')
plt.plot(x_train.numpy(),predict,label = 'Fitting line')
plt.show()

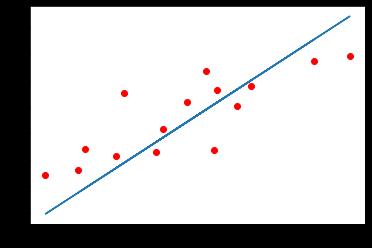
首先需要通过model.eval()将模型变成测试模式，这是因为有一些层操作，比如Dropout和BatchNormalization在训练和测试的时候是不一样的，所以我们需要这样一个操作来转换这些不一样的层的操作。然后将测试数据放入网络进行前向传播得到我们的结果。

这样我们就通过 PyTorch 解决了一个简单的一元回归问题，得到了一条直线去尽可能逼近这些离散的点。

下一章传送门：Note10 多项式回归