pytorch常用优化器总结(包括warmup介绍及代码实现)
Posted 栋次大次
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了pytorch常用优化器总结(包括warmup介绍及代码实现)相关的知识,希望对你有一定的参考价值。
文章目录
优化算法大致分为:梯度下降法,动量优化法,自适应学习率三种。
梯度下降法
梯度下降 GD
通过loss对 ω \\omega ω的一阶导数来找下降方向,并且以迭代的方式来更新参数。
W t + 1 = W t − η ∇ L ( W t ) W_t+1 = W_t-\\eta\\nabla L(W_t) Wt+1=Wt−η∇L(Wt), 其中 η \\eta η为学习率。
随机梯度下降 (SGD)
均匀的随机选择其中一个样本( X ( i ) , Y ( i ) X^(i),Y^(i) X(i),Y(i)),用它代表整个样本,即把它的值乘以N,就相当于获得了梯度的无偏估计值。
公式: W t + 1 = W t − η N ∇ J ( W t , X ( i ) , Y ( i ) ) \\mathbfW_t+1=\\mathbfW_t-\\eta N \\nabla J\\left(\\mathbfW_t, X^(i), Y^(i)\\right) Wt+1=Wt−ηN∇J(Wt,X(i),Y(i))
小批量梯度下降法(MBGD)
每次迭代使用m个样本来对参数进行更新,公式:
W t + 1 = W t − η 1 m ∑ k = i i + m − 1 ∇ J ( W t , X ( k ) , Y ( k ) ) \\mathbfW_t+1=\\mathbfW_t-\\eta \\frac1m \\sum_k=i^i+m-1 \\nabla J\\left(\\mathbfW_t, X^(k), Y^(k)\\right) Wt+1=Wt−ηm1∑k=ii+m−1∇J(Wt,X(k),Y(k))
梯度下降法优点:简单
缺点:训练速度慢,会进入局部极小值点,随机选择梯度的同时会引入噪声,使得权重更新的方向不一定正确
动量优化
SGD+Momentum
增加一个动量,使当前训练数据的梯度受到之前训练数据的影响。
v t = α v t − 1 + η t ∇ J ( W t , X ( i s ) , Y ( i s ) ) W t + 1 = W t − v t \\left\\\\beginarraylv_t=\\alpha v_t-1+\\eta_t \\nabla J\\left(W_t, X^\\left(i_s\\right), Y^\\left(i_s\\right)\\right) \\\\ W_t+1=W_t-v_t\\endarray\\right. vt=αvt−1+ηt∇J(Wt,X(is),Y(is))Wt+1=Wt−vt
加速收敛,有一定摆脱局部最优的能力
但仍具有SGD一部分的缺点
实际中可以尝试
NAG
牛顿加速梯度动量优化方法(NAG, Nesterov accelerated gradient):用上一步的速度先走一小步,再看当前的梯度然后再走一步,
v t = α v t − 1 + η t Δ J ( W t − α v t − 1 ) W t + 1 = W t − v t \\left\\\\beginarraylv_t=\\alpha v_t-1+\\eta_t \\Delta J\\left(W_t-\\alpha v_t-1\\right) \\\\ W_t+1=W_t-v_t\\endarray\\right. vt=αvt−1+ηtΔJ(Wt−αvt−1)Wt+1=Wt−vt
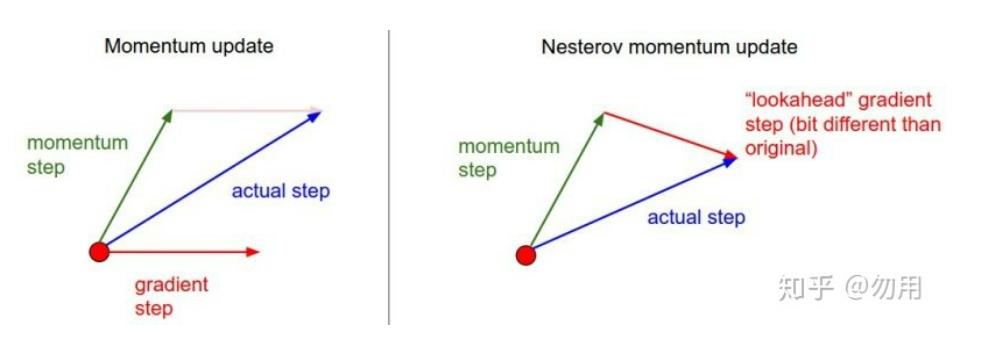
https://zhuanlan.zhihu.com/p/62585696
可以理解为在标准动量中添加一个校正因子。
理解:在momentum中小球会盲目的跟从下坡的梯度,容易发生错误,所以需要一个更聪明的小球,能提前知道它要去哪,还有知道走到坡地的时候速度慢下来,而不是又崇尚另一坡。
优点:梯度下降的方向更加准确
缺点:对收敛率作用不是很大
pytorch中SGD:
模型每次反向传播都会给可学习参数p计算出一个偏导数 g t g_t gt,用于更新对应的参数p。通常 g t g_t gt不会直接作用到对应的可学习参数p上,而是通过优化器做一下处理,得到新的值 g ^ t \\hat g_t g^t,即 F ( g t ) F(g_t) F(gt),然后和学习率lr一起用于更新参数
torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)
参数:
-
params(iterable): iterable of parameters to optimize or dicts defining parameter groups
-
lr(float): 学习率
-
momentum (float, optional) : 动量因子 默认 0。通过上一次的v和当前的偏导数,得到本次的v。即: v t = v t − 1 ∗ m o m e n t u m + g t v_t = v_t-1 * momentum + g_t vt=vt−1∗momentum+gt, 这就是F。
怎么理解:动量使得v具有惯性,这样可以缓和v的抖动,有时可以跳出局部极小。如:上次计算得到v=10,参数更新后本次的偏导是0,那么使用momentum=0.9后,最终用于更新可学习参数的v=9, 而不是0,这样参数仍会得到较大的更新,增加挑出局部极小值的可能性。
-
dampening: 是乘到偏导g上的一个数,即: v t = v t − 1 ∗ m o m e n t u m + g t ∗ ( 1 − d a m p e n i n g ) v_t = v_t-1*momentum + g_t * (1-dampening) vt=vt−1∗momentum+gt∗(1−dampening),dampening在优化器第一次更新时不起作用。
-
weight_decay (float, optional): 权重衰减 (L2 penalty)默认为0,即:L2 正则化,选择合适的权重衰减很重要,需要根据具体的情况取尝试,初步尝试可以选择 1e-4 或者 1e-3。
作用于当前可学习参数p的值,即: g t = g t + ( p ∗ w e i g h t d e c a y ) g_t = g_t + (p*weight_decay) gt=gt+(p∗