leetcode 210. 课程表 II----拓扑排序篇二

Posted 2021-06-23 大忽悠爱忽悠

---

课程表二题解集合

• 引言
• 拓扑排序---BFS
• 邻接矩阵(数组)+ DFS

---

引言

本题是在leetcode 207. 课程表—拓扑排序篇一上，增加了一个记录拓扑序列的功能，因此建议没有看前一篇的同学，先看前一篇，再来阅读本篇

---

拓扑排序—BFS

引言:

• 「拓扑排序」是专门应用于有向图的算法；
• 「拓扑排序」的结果不唯一；
• 删除结点的操作，通过「入度数组」体现，这个技巧要掌握；
• 「拓扑排序」的一个附加效果是：能够顺带检测有向图中是否存在环，这个知识点非常重要，如果在面试的过程中遇到这个问题，要把这一点说出来。

思路:

1、在开始排序前，扫描对应的存储空间（使用邻接表），将入度为 0 的结点放入队列。

2、只要队列非空，就从队首取出入度为 0 的结点，将这个结点输出到结果集中，并且将这个结点的所有邻接结点（它指向的结点）的入度减 1，在减 1 以后，如果这个被减 1 的结点的入度为 0 ，就继续入队。

3、当队列为空的时候，检查结果集中的顶点个数是否和课程数相等即可。

在代码具体实现的时候，除了保存入度为 0 的队列，我们还需要两个辅助的数据结构：

1、邻接表：通过结点的索引，我们能够得到这个结点的后继结点；

2、入度数组：通过结点的索引，我们能够得到指向这个结点的结点个数。

这个两个数据结构在遍历题目给出的邻边以后就可以很方便地得到。

具体的图解，参考: leetcode 207. 课程表—拓扑排序篇一

代码:

class Solution {
public:
	vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites)
	{
		//注意:这里p[1]--->p[0]
		//入度数组:这里入度指的是学习每一门学科前，需要学习的课程数量
		vector<int> inDegree(numCourses, 0);
		//邻接表: 学习完当前课程后，能够去学习的其他课程
		vector<vector<int>> adj(numCourses);
		//计算入度数组和邻接表
		for (auto p : prerequisites)
		{
			inDegree[p[0]]++;
			adj[p[1]].push_back(p[0]);
	   }
		//队列
		queue<int> q;
		//将入度为0的课程都放入队列中去
		for (int i = 0; i < numCourses; i++)
		{
			if (inDegree[i] == 0)
				q.push(i);
		}
		//记录已经出队过的课程数量
		int cnt = 0;
		//设置一个数组用来保存拓扑序列
		vector<int> res;
		//正式计算拓扑序列
		while (!q.empty())
		{
			//获取队头
			int f = q.front();
			//当前队头元素加入拓扑序列数组
			res.push_back(f);
			q.pop();
			cnt++;
			//将队头的所有邻接点的入度减去一，然后判断是否为0，为0就入队
			for (auto p : adj[f])
			{
				if (--inDegree[p] == 0) q.push(p);
			 }
		}
		if (cnt == numCourses)return res;
		return vector<int>();
	}
};

---

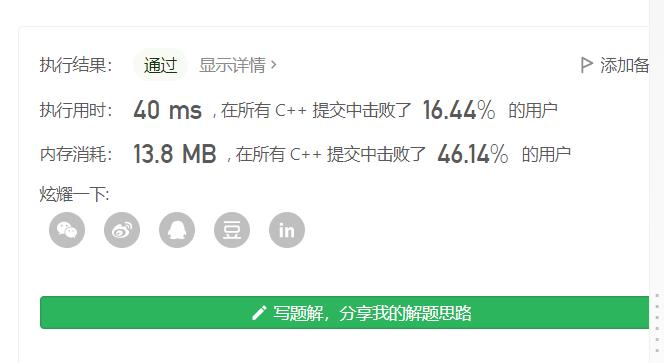
邻接矩阵(数组)+ DFS

思路:

第 1 步：构建逆邻接表；

第 2 步：递归处理每一个还没有被访问的结点，具体做法很简单：对于一个结点来说，先输出指向它的所有顶点，再输出自己。

第 3 步：如果这个顶点还没有被遍历过，就递归遍历它，把所有指向它的结点都输出了，再输出自己。注意：当访问一个结点的时候，应当先递归访问它的前驱结点，直至前驱结点没有前驱结点为止。

代码:

class Solution {
public:
	vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites)
	{
		//注意:这里p[1]--->p[0]
        //邻接矩阵:记录学习完当前课程后，可以去学习什么课程
		vector<vector<int>> adj(numCourses);
		//计算邻接矩阵
		for (auto p : prerequisites)
			adj[p[1]].push_back(p[0]);
		//marked数组，标记当前点是正在访问，还是处于访问过了的状态
		vector<int> marked(numCourses, 0);
        //stack栈来保存拓扑序列
		stack<int> res;
		//以每一个课程为起点，对他的所有邻接点进行遍历操作
		for (int i = 0; i < numCourses; i++)
		{
			// 注意方法的语义，如果图中存在环，表示课程任务不能完成，应该返回空数组
			if (dfs(i, adj, marked, res))
				return vector<int>();
		}
		// 在遍历的过程中，一直 dfs 都没有遇到已经重复访问的结点，就表示有向图中没有环
	  // 所有课程任务可以完成，应该返回 true
	  // 下面这个断言一定成立，这是拓扑排序告诉我们的结论
		//res.size() == numCourses;


		 // 想想要怎么得到结论，我们的 dfs 是一致将后继结点进行 dfs 的
		// 所以压在栈底的元素，一定是那个没有后继课程的结点
		// 那个没有前驱的课程，一定在栈顶，所以课程学习的顺序就应该是从栈顶到栈底
		// 依次出栈就好了
		vector<int> ret;
		for (int i = 0; i < numCourses; i++)
		{
			ret.push_back(res.top());
			res.pop();
		}
		return ret;
	}
/**
 * 注意这个 dfs 方法的语义
 *
 * @param i      当前访问的课程结点
 * @param graph
 * @param marked 如果 == 1 表示正在访问中，如果 == 2 表示已经访问完了
 * @return true 表示图中存在环，false 表示访问过了，不用再访问了
 */
	bool dfs(int i,vector<vector<int>>& adj,vector<int>& marked,stack<int>& res)
	{
		// 如果访问过了，就不用再访问了
		if (marked[i] == 1) 
			// 从正在访问中，到正在访问中，表示遇到了环
			return true;
		// 表示在访问的过程中没有遇到环，这个节点访问过了
		if (marked[i] == 2) return false;
		// 走到这里，是因为初始化呢，此时 marked[i] == 0
       // 表示正在访问中
		marked[i] = 1;
		//遍历当前点的后继节点
		for (auto p : adj[i])
		{
			// 层层递归返回 true ，表示图中存在环
			if (dfs(p, adj, marked, res))
				return true;
		}
		// i 的所有后继结点都访问完了，都没有存在环，则这个结点就可以被标记为已经访问结束
	 // 状态设置为 2
		marked[i] = 2;
		res.push(i);
		// false 表示图中不存在环
		return false;
	}
};