洛谷-----P5534 XR-3等差数列

Posted 2021-06-15 大忽悠爱忽悠

等差数列题解集合

• 公式法
• dfs

---

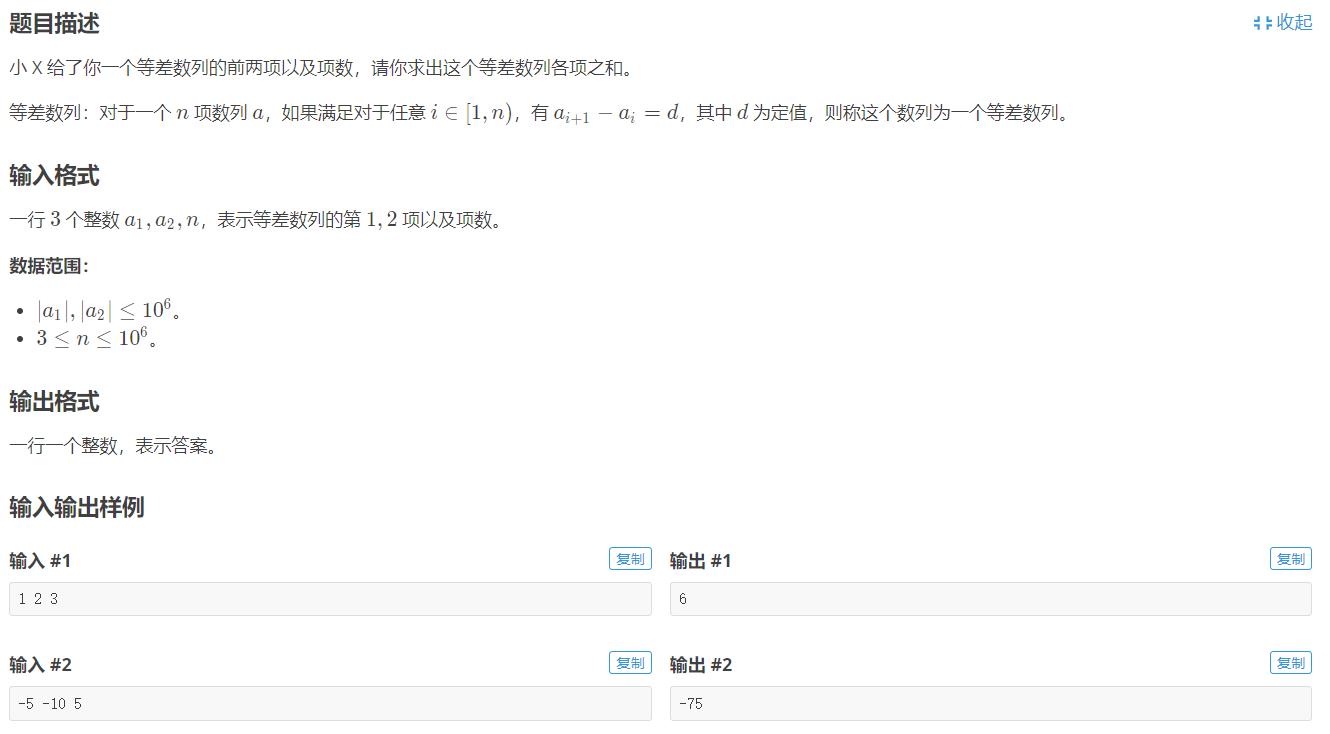
公式法

套用数学上面的等差数列求和公式:Sn=a1*n+n(n-1)*d/2

末项公式：Sn = a1 + (n - 1) * d;

代码:

#include<iostream>
using namespace std;
class Solution {
public:
	long solution(long a1,long a2,long n)
	{
		long d = a2 - a1;
		return a1 * n + n * (n - 1) * d / 2;
	}
};
int main()
{
	Solution s;
	long a1, a2, n;
	cin >> a1 >> a2 >> n;
	cout << s.solution(a1, a2, n) << endl;
	return 0;
}

---

dfs

思路:

还是将问题树形化，化成对一颗树的遍历，这样就很方便写出递归的代码

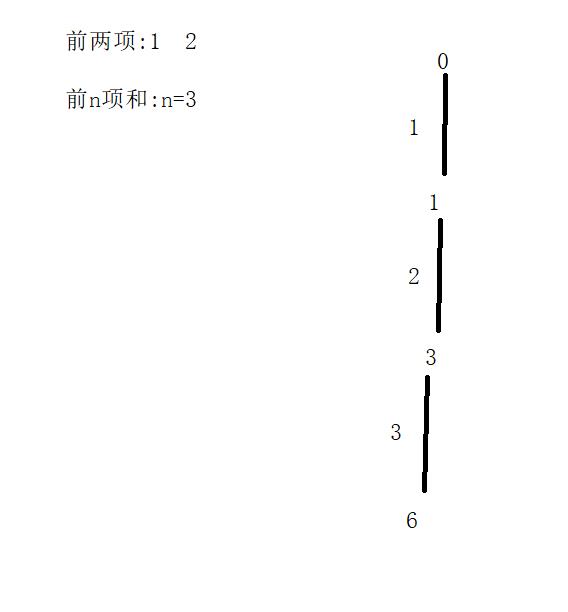
显然这里是对一叉树的遍历，递归过程中我们需要求出当前所要累加上去的当前项的值，当前项的值可以通过递推公式求出来，即an=a1+(n-1)*d

代码:

#include<iostream>
using namespace std;
class Solution {
public:
	long solution(long a1,long d,long max)
	{
		if (abs(a1) > abs(max)) return 0;
		return solution(a1 + d, d, max)+a1;
	}
};
int main()
{
	Solution s;
	long a1, a2, n;
	cin >> a1 >> a2 >> n;
	long d = a2 - a1;
	//递归结束条件，累加到第n项
	long max = a1 + (n - 1) * d;
	cout << s.solution(a1,d,max)<< endl;
	return 0;
}

超时了