洛谷——P1349 广义斐波那契数列

Posted 2020-10-11

题目描述

广义的斐波那契数列是指形如an=p*an-1+q*an-2的数列。今给定数列的两系数p和q，以及数列的最前两项a1和a2，另给出两个整数n和m，试求数列的第n项an除以m的余数。

输入输出格式

输入格式：

 

输入包含一行6个整数。依次是p,q,a1,a2,n,m，其中在p,q,a1,a2整数范围内，n和m在长整数范围内。

 

输出格式：

 

输出包含一行一个整数，即an除以m的余数。

 

输入输出样例

输入样例#1：

1 1 1 1 10 7

输出样例#1：

6

说明

数列第10项是55，除以7的余数为6。

 

我们来通过这个题讲一下斐波那契数列怎么用矩阵乘法来优化吧 

我们知道对于斐波那契数列我们有这样的递推式：f[n]=f[n-1]+f[n-2]

通常情况下，我们计算f(n)的时间复杂度就是O(n)（分别计算f(1), f(2) ... f(n - 1)）.
但是当n很大又或者还有其他处理的复杂度一叠加便会超时。

所以当n很大的时候，我们的递推式便不起作用了，我们应该像一种办法来优化一下这个递推式，怎么办呢，我们看到这个式子有加，有乘，我们就一般会想到矩阵乘法（这时候就有人会问了，博主，你眼瞎啊，明明就是个加法的式子，你说他有乘法。。。）额、、对于这个问题，我们可以将上面的式子做一个小小的变形，将它变成f[n]=f[n-1]*1+f[n-2]*1,      f[n-1]=f[n-1]*1+f[n-2]*0

我们在这个地方普及一下矩阵乘法优化递推式的特征：形如f(n) = a1 * f(n - 1) + a2 * f(n - 2) + ... + ak * f(n - k)+c (c为常数）

 

 然后我们可以将他组成这样的一个矩阵

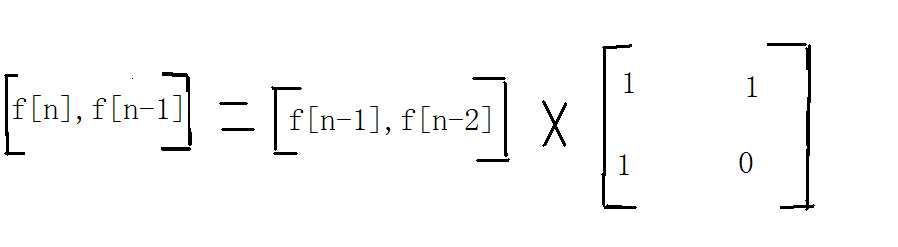
然后我们进行矩阵乘法

来，看看代码：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 100000000
using namespace std;
int n;
int read()
{
    int x=0,f=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar();
    return x*f;
}
struct Node
{
    long long m[3][3];
    Node(){memset(m,0,sizeof(m));}
}mb,ans;
int GCD(int a,int b)
{
    if(b==0) return a;
    return GCD(b,a%b);
}
Node operator*(Node a,Node b)
{
    Node c;
    for(int i=1;i<=2;i++)
     for(int j=1;j<=2;j++)
      for(int k=1;k<=2;k++)
       c.m[i][j]=(c.m[i][j]%mod+a.m[i][k]*b.m[k][j]%mod)%mod;
    return c;
}
int main()
{
    n=read();n--;
    mb.m[1][1]=mb.m[1][2]=mb.m[2][1]=1;
    ans.m[1][1]=ans.m[2][2]=1;
    while(n)
    {
        if(1&n) ans=ans*mb;
        mb=mb*mb;n>>=1;
    }
    cout<<ans.m[1][1];
    return 0;
}

矩阵乘法优化斐波那契

 

 

 

对于这个式子，我们可以根据朴素的斐波那契的矩阵乘法的形式将式子推出来

 

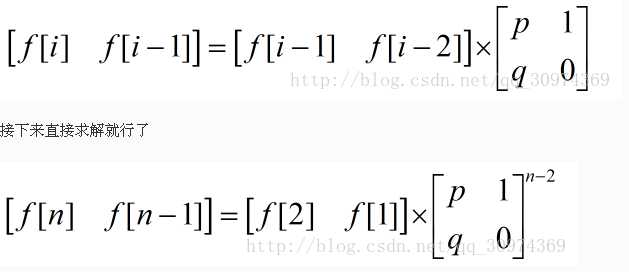
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
long long q,p,a1,a2,n,mod;
long long read()
{
    long long x=0,f=1; char ch=getchar();
    while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();}
    while(ch>=‘0‘&&ch<=‘9‘) x=x*10+ch-‘0‘,ch=getchar();
    return x*f;
}
struct Node 
{
    long long m[3][3];
    Node(){memset(m,0,sizeof(m));}
}begin,ans;
Node operator*(Node a,Node b)
{
    Node c;
    for(int i=1;i<=2;i++)
     for(int j=1;j<=2;j++)
      for(int k=1;k<=2;k++)
       c.m[i][j]=(c.m[i][j]%mod+(a.m[i][k]%mod*b.m[k][j]%mod)%mod)%mod;
    return c;
}
int main()
{
    p=read(),q=read(),a1=read(),a2=read();
    n=read(),mod=read();n-=2;
    ans.m[1][1]=a2,ans.m[1][2]=a1;
    begin.m[1][1]=p,begin.m[2][1]=q,begin.m[1][2]=1;
    while(n)
    {
        if(n&1) ans=ans*begin;
        begin=begin*begin;
        n>>=1;
    }
    if(n+2==1) cout<<ans.m[1][2]%mod;
    else cout<<ans.m[1][1]%mod;
    return 0;
}