Python编程实现Gauss-Seidel（高斯-赛德尔）方法计算金属板内网格温度分布

Posted 2021-06-09 Jing Sir

原理过程参照：

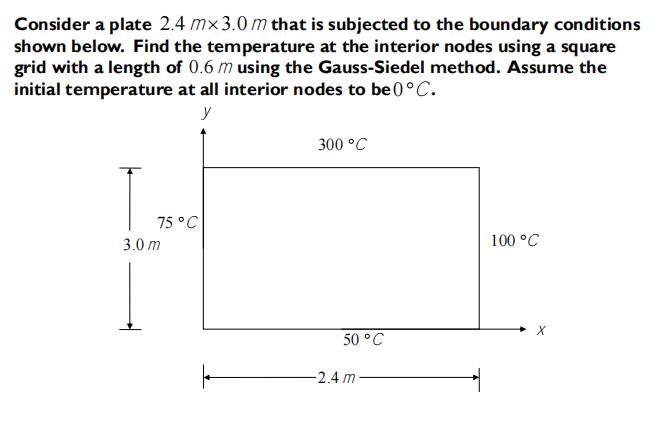
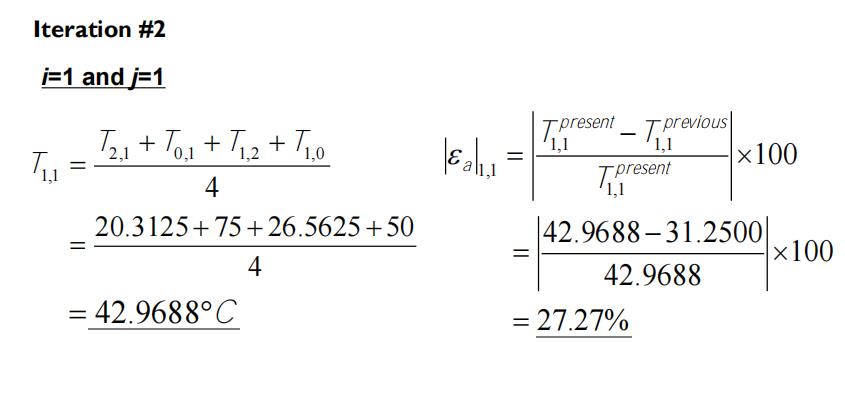
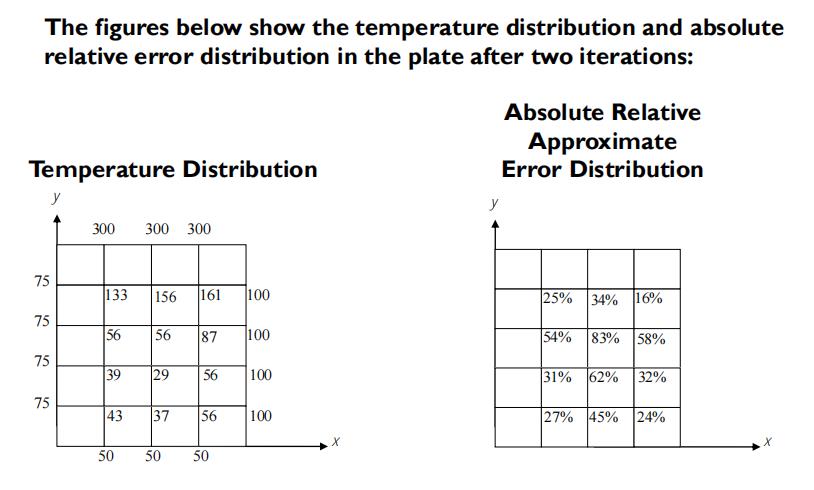
函数实现过程：

#假定金属板为矩形；
#内部初始温度为0度(℃)；
#x，y为金属板的长宽(m)；
#del_x，del_y分别为划分步长；
#t1,t2,t3,t4分别为左、上、右、下的初始温度；

#函数实现过程
def Gauss_Seidel(x,y,del_x,del_y,t1,t2,t3,t4,k):
    poi_x = int(x/del_x)+1 #x轴划分点数
    poi_y = int(y/del_y)+1 #y轴划分点数
    err = np.zeros((k-1,poi_x,poi_y),dtype = np.float32)#err为绝对相对误差维系矩阵；
    Temp = np.zeros((k,poi_x,poi_y),dtype = np.float32)#Temp为温度记录矩阵；
    #赋予初始条件
    for n in range (k):
        for i in range (poi_x):
            for j in range (poi_y):
                Temp[n][0][j] = t1 #左侧温度
                Temp[n][i][poi_y-1] = t2 #上方温度
                Temp[n][poi_x-1][j] = t3 #右侧温度
                Temp[n][i][0] = t4 #下方温度
    #for n in range (k):
    print("赋予初始条件\\n")
    print(Temp[0])
    print("\\n\\n\\n")
    
    #计算迭代过程中节点温度
    for n in range (k):
        for i in range (1,poi_x-1):
            for j in range (1,poi_y-1):
                Temp[n][i][j] = (Temp[n][i+1][j]+Temp[n][i-1][j]+Temp[n][i][j+1]+Temp[n][i][j-1])/4.0
                if(n+1<k):
                    Temp[n+1] = Temp[n]#模拟迭代过程
                    #Temp[n+1][i][j] = (Temp[n][i+1][j]+Temp[n][i-1][j]+Temp[n][i][j+1]+Temp[n][i][j-1])/4.0
    #for n in range (k):
    print("计算迭代过程并记录\\n")
    print(Temp)
    print("\\n\\n\\n")
    
    #计算次间绝对相对误差
    for n in range (k-1):
        for i in range (1,poi_x-1):
            for j in range (1,poi_y-1):
                err[n][i][j] = abs((Temp[n+1][i][j]-Temp[n][i][j])/Temp[n+1][i][j])
    #for n in range (k-1):
    print("计算每一步与上一步的绝对相对误差\\n")
    print(err)
    print("\\n\\n\\n")

实验结果验证：

迭代一次与迭代两次进行比较

改变迭代次数(k=10)：

第十次与第九次进行比较：

最后两次间的绝对相对误差：

完整代码：

import numpy as np
import math 

#假定金属板为矩形；
#内部初始温度为0度(℃)；
#x，y为金属板的长宽(m)；
#del_x，del_y分别为划分步长；
#t1,t2,t3,t4分别为左、上、右、下的初始温度；

#初始
x = 2.4
y = 3.0
del_x = 0.6
del_y = 0.6

t1 = 75
t2 = 300
t3 = 100
t4 = 50

#k为迭代次数；
k = 2

#函数实现过程
def Gauss_Seidel(x,y,del_x,del_y,t1,t2,t3,t4,k):
    poi_x = int(x/del_x)+1 #x轴划分点数
    poi_y = int(y/del_y)+1 #y轴划分点数
    err = np.zeros((k-1,poi_x,poi_y),dtype = np.float32)#err为绝对相对误差维系矩阵；
    Temp = np.zeros((k,poi_x,poi_y),dtype = np.float32)#Temp为温度记录矩阵；
    #赋予初始条件
    for n in range (k):
        for i in range (poi_x):
            for j in range (poi_y):
                Temp[n][0][j] = t1 #左侧温度
                Temp[n][i][poi_y-1] = t2 #上方温度
                Temp[n][poi_x-1][j] = t3 #右侧温度
                Temp[n][i][0] = t4 #下方温度
    #for n in range (k):
    print("赋予初始条件\\n")
    print(Temp[0])
    print("\\n\\n\\n")
    
    #计算迭代过程中节点温度
    for n in range (k):
        for i in range (1,poi_x-1):
            for j in range (1,poi_y-1):
                Temp[n][i][j] = (Temp[n][i+1][j]+Temp[n][i-1][j]+Temp[n][i][j+1]+Temp[n][i][j-1])/4.0
                if(n+1<k):
                    Temp[n+1] = Temp[n]#模拟迭代过程
                    #Temp[n+1][i][j] = (Temp[n][i+1][j]+Temp[n][i-1][j]+Temp[n][i][j+1]+Temp[n][i][j-1])/4.0
    #for n in range (k):
    print("计算迭代过程并记录\\n")
    print(Temp)
    print("\\n\\n\\n")
    
    #计算次间绝对相对误差
    for n in range (k-1):
        for i in range (1,poi_x-1):
            for j in range (1,poi_y-1):
                err[n][i][j] = abs((Temp[n+1][i][j]-Temp[n][i][j])/Temp[n+1][i][j])
    #for n in range (k-1):
    print("计算每一步与上一步的绝对相对误差\\n")
    print(err)
    print("\\n\\n\\n")

#执行
#k = 2
Gauss_Seidel(x,y,del_x,del_y,t1,t2,t3,t4,k)

#增加迭代次数对比
k = 10
Gauss_Seidel(x,y,del_x,del_y,t1,t2,t3,t4,k)

#修改步长参数，增加分块
del_x = 0.3 
del_y = 0.3
k = 5 #d迭代次数
Gauss_Seidel(x,y,del_x,del_y,t1,t2,t3,t4,k)