Jacobi迭代法与Gauss-Seidel迭代法

Posted 2020-06-08 白马负金羁

之前我在博客里介绍过牛顿-拉弗逊迭代法，对数据挖掘技术熟悉的同学应该还知道有梯度下降法（其实也是一种迭代算法）。今天刚好有朋友和我讨论泊松图像融合算法，我说我过去文章里给出的是最原始、最直观的实现算法。对于理解泊松融合的原理比较有帮助，但是效率可能并不理想。印象中，泊松融合是有一个以矩阵为基础的快速算法的。但是过去我浅尝辄止了，也没深究，今天刚好再提到，小看了一下，似乎涉及高斯-塞德尔迭代法。好吧，博主君暂且把知道的这部分内容做个介绍吧。特别说明：以下内容主要取材自《数值方法（MATLAB版）（第四版）》马修斯等著，电子工业出版社2010年出版发行。

一、雅各比迭代法

考虑如下方程组：

$$4x-y+z=7\\4x-8y+z=-21\\-2x+y+5z=15$$
上述方程可表示成如下形式：
$$x=\frac{7+y-z}{4} \\y=\frac{21+4x+z}{8}\\z=\frac{15+2x-y}{5}$$
这样就提出了下列雅可比迭代过程：

$$\begin{aligned} x_{k+1} & =\frac{7+y_k+z_k}{4} \y_{k+1} & =\frac{21+4x_k+z_k}{8} & (3) \z_{k+1} & =\frac{15+2x_k-y_k}{5} \end{aligned}$$

如果从$P_0=(x_0,y_0,z_0)=(1,2,2)$开始，则上式中的迭代将收敛到解$(2,4,3)$。

将$x_0=1,y_0=2$和$z_0=2$代入上式中每个方程的右边，即可得到如下新值：

$$x_1=\frac{7+2-2}{4}=1.75\\y_1=\frac{21+4+2}{8}=3.375\\z_1=\frac{15+2-2}{5}=3.00$$

新的点$P_1=(1.75,3.375,3.00)$比$P_1$更接近$(2,4,3)$。使用迭代过程（3）生成点的序列{$P_0$}将收敛到解$(2,4,3)$。

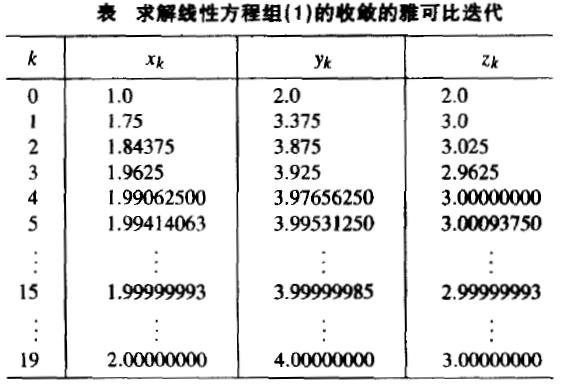
这个过程称为雅可比迭代，可用来求解某些类型的线性方程组。从上表中可以看出，经过19步选代，选代过程收敛到一个精度为9 位有效数字的近似值（2.00000000， 4.00000000， 3.00000000）。但有时雅可比迭代法是无效的。通过下面的例子可以看出，重新排列初始线性方程组后，应用雅可比迭代法可能会产生一个发散的点的序列。

设重新排列的线性方程组如下：

?2x+y+5z=154x?8y+z=?214多线性方程组迭代算法——Jacobi迭代算法的Python实现

数值分析中的Jacobi及Gauss-Seidel迭代中的矩阵L ,U ,D,分别是哪三个单词?

多线性方程组迭代算法——Gauss-Seidel迭代算法的Python实现

《数值分析》-- 雅可比迭代法高斯—塞德尔迭代法

《数值分析》-- 雅可比迭代法高斯—塞德尔迭代法

《数值分析》-- 雅可比迭代法高斯—塞德尔迭代法