矩阵——矩阵的秩
Posted 炫云云
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了矩阵——矩阵的秩相关的知识,希望对你有一定的参考价值。
矩阵的秩
定 义 1 \\large\\color{magenta}{\\boxed{\\color{brown}{定义1 } }} 定义1 在 m × n m×n m×n矩阵中,任取 k k k行与 k k k列( k ≤ m , k ≤ n k≤m,k≤n k≤m,k≤n),位于这些行列交叉处的 k 2 k^2 k2 个元素,不改变它们在A中所处的位置次序而得到的 k k k阶行列式,称为矩阵 A A A的 k k k阶子式.
定 义 2 \\large\\color{magenta}{\\boxed{\\color{brown}{定义2 } }} 定义2 设在矩阵 A A A中有一个不等于0的 k k k阶子式,且所有 k + 1 k+1 k+1阶子式(如果存在的话)全等于0,则数 k k k称为矩阵的秩,即矩阵中不等于0的最高阶子式的阶数就是矩阵的秩,记作 r ( A ) r(A) r(A),即 r ( A ) = k r(A)= k r(A)=k.
规定零矩阵的秩等于0.
注 : \\Large\\color{violet}{注:} 注:可逆矩阵又称为满秩矩阵,不可逆矩阵又称为降秩矩阵.
子式是行列式,如果A是一个3×4矩阵,它的一个2阶子式和一个3阶子式是:
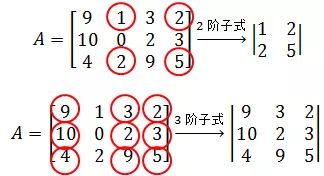
说 明 : \\Large\\color{violet}{说明:} 说明: (1) 对任意矩阵 A A A, 其秩总是存在且惟一的.
给定某 6 行 8 列矩阵 A , A A, A A,A 最多有6阶子式 ⇒ R ( A ) ≤ 6 \\Rightarrow R(A) \\leq 6 ⇒R(A)≤6 .
若 A A A 的 C 8 6 C_{8}^{6} C86 个 6 阶子式中有一个非 0 ⇒ R ( A ) = 6. 0 \\Rightarrow R(A)=6 . 0⇒R(A)=6.
若 A A A 的 6 阶子式都为0,考察 A A A 的 C 8 5 C 6 5 C_{8}^{5} C_{6}^{5} C85C65 个5阶子式,
若某 5 阶子式非 0 ⇒ R ( A ) = 5. 0 \\Rightarrow R(A)=5 . 0⇒R(A)=5.
如此继续, 总可以求得矩阵 A A A 唯一的秩.
(2) 仅由定义来确定矩阵的秩,其计算量巨大
为证明某矩阵 A A A 的秩 R ( A 100 × 90 ) = 50 R\\left(A_{100 \\times 90}\\right)=\\mathbf{5 0} R(A100×90)=50 :
需要从 A A A 的 C 100 50 C 90 50 C_{100}^{50} C_{90}^{50} C10050C9050 个 50 阶子式中找出一个非零者;
需证明所有 51 , 52 , ⋯ , 90 \\mathbf{5 1 , 5 2 , \\cdots , 9 0} 51,52,⋯,90 阶子式均为 0.
(3) A A A 的 k k k 阶子式全为 0 ⇒ k + 1 0 \\Rightarrow k+1 0⇒k+1 阶子式全为 0. 0 . 0.
A A A 的 k + 1 \\boldsymbol{k}+1 k+1 阶子式 = 子式中第1行元与相应代数余子式 乘积之和
每个代数余子式都是 A A A 的带符号的 k k k 阶子式,为0!
例
1
\\Large\\color{violet}{例1 }
例1 .求矩阵的秩:(1)
A
=
(
2
4
8
1
2
0
)
A=\\left(\\begin{array}{lll}2 & 4 & 8 \\\\ 1 & 2 & 0\\end{array}\\right)
A=(214280) (2)
B
=
(
1
2
4
1
2
4
8
2
3
6
2
0
)
B=\\left(\\begin{array}{llll}1 & 2 & 4 & 1 \\\\ 2 & 4 & 8 & 2 \\\\ 3 & 6 & 2 & 0\\end{array}\\right)
B=⎝⎛123246482120⎠⎞.
解:显然
A
A
A 的秩为 2.
对
B
的任一
3
阶子式,其前两行总成比例, 为
0
⇒
R
(
B
)
<
3
B
有一个
2
阶子式
∣
8
2
2
0
∣
≠
0
⇒
R
(
B
)
≥
2
}
⇒
R
(
B
)
=
2
\\left.\\begin{array}{l}\\text { 对 } B \\text { 的任一 } 3 \\text { 阶子式,其前两行总成比例, 为 } 0 \\Rightarrow R(B)<3 \\\\ B \\text { 有一个 } 2 \\text { 阶子式 }\\left|\\begin{array}{ll}8 & 2 \\\\ 2 & 0\\end{array}\\right| \\neq 0 \\Rightarrow R(B) \\geq 2\\end{array}\\right\\} \\Rightarrow R(B)=2
对 B 的任一 3 阶子式,其前两行总成比例, 为 0⇒R(B)<3B 有一个 2 阶子式 ∣∣∣∣8220∣∣∣∣=0⇒R(B)≥2⎭⎬⎫⇒R(B)=2
思考: 设某矩阵
A
A
A 的秩为
3.
3 .
3.
(1) A A A 的所有 3 阶子式都不为 0 吗?
(2) A A A 的所有 2 阶子式可以都为 0 吗?
矩阵的秩的作用
在行列式的意义中我们提到:向量间最重要的关系就是独立或不独立,行列式是否等于0正是这种关系的有效描述。由此看来,矩阵的秩 r ( A ) = k r(A) = k r(A)=k 表示矩阵中一定存在一个 k k k阶行列式,这个行列式中的向量全部独立;且矩阵中对于任意 k + 1 k+1 k+1阶子式,都存在至少一个多余的向量。简言之,秩意味着矩阵中有且仅有 k k k 个独立向量。
关于秩的常用结论
(I)
r
(
A
n
×
n
)
=
n
⇔
∣
A
∣
≠
0
r\\left(A_{n \\times n}\\right)=n \\Leftrightarrow|A| \\neq 0
r(An×n)< 以上是关于矩阵——矩阵的秩的主要内容,如果未能解决你的问题,请参考以下文章