傅里叶变换的相关函数（笔记02）

Posted 2021-06-02 月疯

 

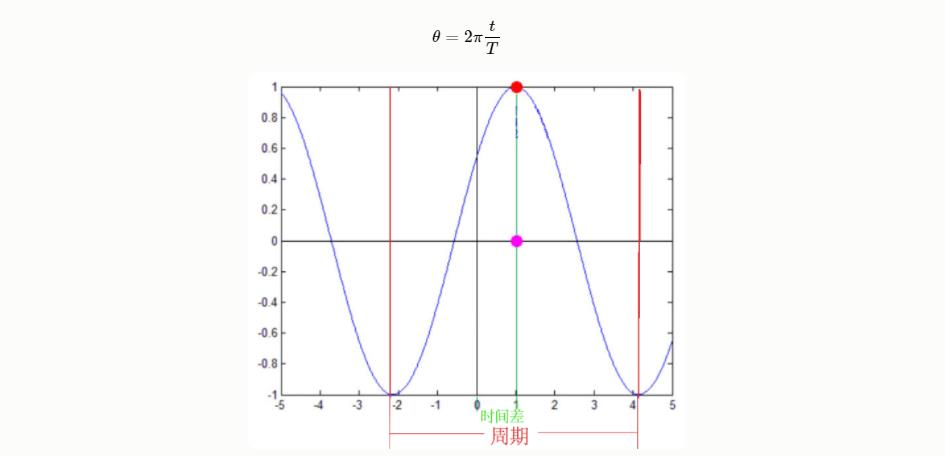
三角函数的标准式：

y=Acos(ωx+θ)+ky=Acos⁡(ωx+θ)+k

AA代表振幅，函数周期是2πw2πw，频率是周期的倒数w2πw2π，θθ是函数初相位，kk在信号处理中称为直流分量。这个信号在频域就是一条竖线。

我们再来假设有一个比较复杂的时域函数y=f(t)y=f(t)，根据傅里叶的理论，任何一个周期函数可以被分解为一系列振幅A，频率ωω或初相位θθ正弦函数的叠加

y=A1sin(ω1t+θ1)+A2sin(ω2t+θ2)+A3sin(ω3t+θ3)

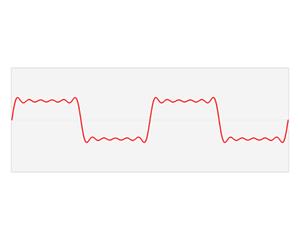
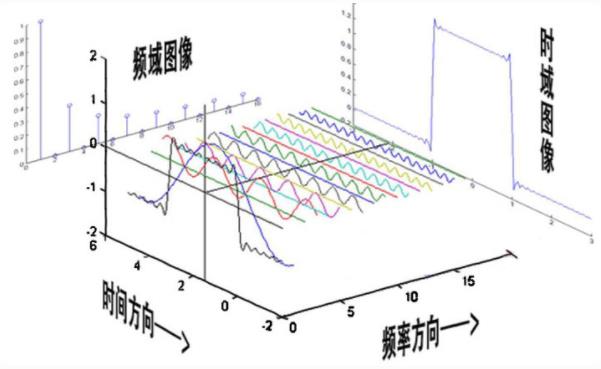
傅里叶变换可以把一个比较复杂的函数转换为多个简单函数的叠加，将时域（即时间域）上的信号转变为频域（即频率域）上的信号，看问题的角度也从时间域转到了频率域，因此在时域中某些不好处理的地方，在频域就可以较为简单的处理，这就可以大量减少处理信号计算量。信号经过傅里叶变换后，可以得到频域的幅度谱以及相位谱，信号的幅度谱和相位谱是信号傅里叶变换后频谱的两个属性。

假设我们的输入信号的函数是：

 

S=0.2+0.7∗cos(2π∗50t+20/180π)+0.2∗cos(2π∗100t+70/180π)

直流分量是0.2，以及两个余弦函数的叠加，余弦函数的幅值分别为0.7和0.2，频率分别为50和100，初相位分别为20度和70度。

freqs = np.fft.fftfreq(采样数量, 采样周期)　　通过采样数与采样周期得到时域序列经过傅里叶变换后的频率序列

np.fft.fft(原序列)　　原函数值的序列经过快速傅里叶变换得到一个复数数组，复数的模代表的是振幅，复数的辐角代表初相位

np.fft.ifft(复数序列)　　复数数组 经过逆向傅里叶变换得到合成的函数值数组

通过上面的基本知识进行python编程练习：

import matplotlib.pyplot as plt
import numpy as np
import numpy.fft as fft
import math

plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示符号

Fs = 1000;  # 采样频率
T = 1 / Fs;  # 采样周期
L = 1000;  # 信号长度
t = [i * T for i in range(L)]#获取时间序列
t = np.array(t)
#原始信号
S = 0.2 + 0.7 * np.cos(2 * np.pi * 50 * t + 20 / 180 * np.pi) + 0.2 * np.cos(2 * np.pi * 100 * t + 70 / 180 * np.pi);

#进行傅里叶变换获取振幅和相位角
complex_array = fft.fft(S)
print(complex_array.shape)  # (1000,)
print(complex_array.dtype)  # complex128
print(complex_array[1])  # (-2.360174309695419e-14+2.3825789764340993e-13j)

#################################
plt.subplot(311)##把画布分成3*1的格子，把Y1放在第一格
plt.grid(linestyle=':')
#获取下标1-51的数据
plt.plot(1000 * t[1:51], S[1:51], label='S')  # y是1000个相加后的正弦序列
plt.xlabel("t（毫秒）")
plt.ylabel("S(t)幅值")
plt.title("叠加信号图")
plt.legend()

###################################
plt.subplot(312)#把画布分成3*1的格子，把Y2放在第二格
#进行傅里叶的逆变换
S_ifft = fft.ifft(complex_array)
# S_new是ifft变换后的序列
plt.plot(1000 * t[1:51], S_ifft[1:51], label='S_ifft', color='orangered')
plt.xlabel("t（毫秒）")
plt.ylabel("S_ifft(t)幅值")
plt.title("ifft变换图")
plt.grid(linestyle=':')
plt.legend()

###################################
# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅（能量大小）
pows = np.abs(complex_array)
#分别获取复数的实部和虚部
sita = math.atan2(np.real(complex_array),np.imag(complex_array))
print(sita)

plt.subplot(313)
plt.title('FFT变换,频谱图')
plt.xlabel('Frequency 频率')
plt.ylabel('Power 功率')
plt.tick_params(labelsize=10)
plt.grid(linestyle=':')
plt.plot(freqs[freqs > 0], pows[freqs > 0], c='orangered', label='Frequency')
plt.legend()
plt.tight_layout()
plt.show()

效果展示：

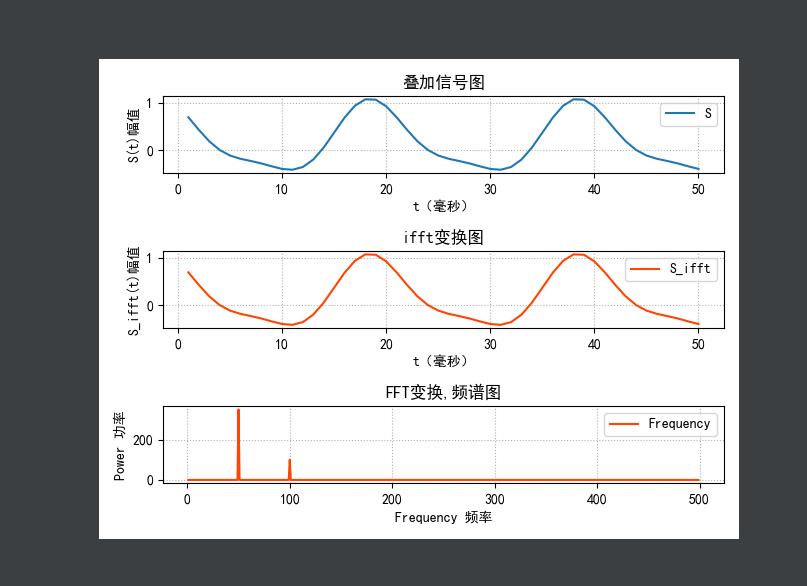
频率、幅值、初相角获取

# 得到分解波的频率序列
freqs = fft.fftfreq(t.size, t[1] - t[0])
# 复数的模为信号的振幅（能量大小）
pows = np.abs(complex_array)
#分别获取复数的实部和虚部，初相角
sita = math.atan2(np.real(complex_array),np.imag(complex_array))