傅里叶变换和拉普拉斯变换学习笔记

Posted 2022-12-01 嗑药的皮皮虾

欧拉公式

欧拉公式将三角函数和指数函数联系起来
复指数函数代表一个旋转的圆，自变量是时间t，角频率代表旋转速度。

傅里叶变换（轻量版拉普拉斯变换）

定义
f(t）是t的函数，如果t满足狄里赫莱条件：
(1) 函数在任意有限区间内连续，或只有有限个第一类间断点;
(2)在一个周期内，函数有有限个极大值或极小值。
(3) x(t)在单个周期内绝对可积，即

则有下式成立，称为积分运算f(t）的傅立叶变换。

F（ω）叫做f(t）的像函数，f(t）叫做F（ω）的像原函数。F（ω）是f(t）的像。f(t）是F（ω）原像。

间断点的分类
设f(x)在x=a处间断，则
(1) 若f(a-0),f(a+0)都存在，称x=a为f(x)的第一类间断点，其中：

1. 若f(a-0)=f(a+0)!=f(a),称x=a为可去间断点；

2. 若f(a-0)!=f(a+0),称x=a为跳跃间断点。

(2) 若f(a-0),f(a+0)中至少有一个不存在，称x=a为f(x)的第二类间断点

拉普拉斯变换

因为有些函数不满足绝对可积条件，所以不能进行傅里叶变换。
把不满足绝对的可积的函数乘以一个快速衰减的函数，这样在趋于无穷 时原函数也衰减到零了，从而满足绝对可积。

通过上图的变换就得到拉普拉斯变换公式

通过拉普拉斯变换将一个函数从时域转换到频域，求一个函数的拉普拉斯变换通常都是用公式和性质求解的，很少用定义求解。

留数法进行拉普拉斯反变换

用留数法进行拉氏反变换的关键在于将变换式进行部分分式展开，然后逐项查表进行反变换。设L(s)是s的有理真分式

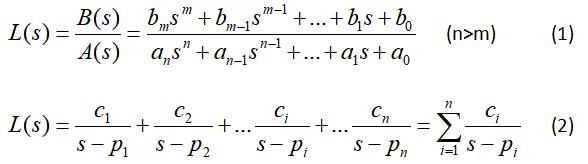
思路：将(1)式化简为(2)式，然后利用基本公式得到拉氏反变换

式(1)中系数a,b,c都是实常数；n,m是正整数。按留数定理可将L(s)展开为部分分式。分以下两种情况讨论。
1、A(s)=0无重根
可将L(s)写成n个简单的部分分式和，如式(2)

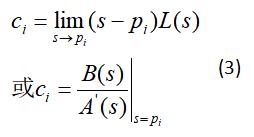
然后根据式(3)求出系数c，再利用基本公式得到拉氏反变换，如式(4)。

2、A(s)=0有重根

p1为L(s)的r重根，pr+1…pn为L(s)的n-r个单根，如式(5).
重根的系数cr…cr-1按式(6)计算，单根的系数cr+1…cn仍按式(3)计算

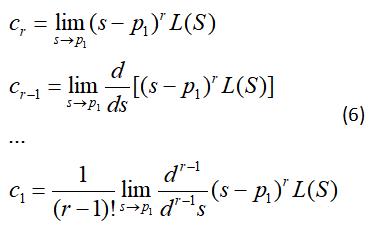
求出系数c后就可以进行拉氏反变换

本文引用了 https://zhuanlan.zhihu.com/p/40783304 的部分图片