解题报告CF DIV2 #ROUND 721 A~C

Posted 鱼竿钓鱼干

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了解题报告CF DIV2 #ROUND 721 A~C相关的知识，希望对你有一定的参考价值。

【解题报告】CF DIV2 #ROUND 721 A~C

比赛链接

比赛评价：
A题码了后实在太累了，明天还要早训就没交题，白天补的题目。
各位还是要注意身体健康呀，这几天感觉确实不大对劲。

A. And Then There Were K

题意
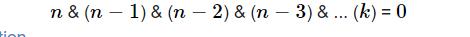
在这里插入图片描述
找到最大的k满足上面的式子

思路
比较简单1发AC
先暴力打了一遍程序找的规律
a n s = 2 i n t ( l o g 2 k ) − 1 ans=2^{int(log_2k)}-1 ans=2int(log2​k)−1
不过据说有人用pow实现的，然后WA了

代码

// Problem: A. And Then There Were K
// Contest: Codeforces - Codeforces Round #721 (Div. 2)
// URL: https://codeforces.com/contest/1527/problem/A
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// FishingRod

#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY

*/
int T;
LL quick(LL a,LL b)
{
    LL res=1;
    a=a;
    while(b)
    { 
        if(b&1) res=(res*a);
        a=(a*a);
        b>>=1;
    }
    return res;
}
void solve(int C)
{
	//NEW DATA CLEAN
	
	//NOTE!!!
	int n;cin>>n;
	int k=int(log2(n));
	cout<<quick(2,k)-1<<endl;
}

int main()
{
	#ifdef MULINPUT
		scanf("%d",&T);
		for(int i=1;i<=T;i++)solve(i);
	#else
		solve(1);
	#endif
	return 0;
}

B1. Palindrome Game (easy version)

字符串+博弈论

题意
easy version初始给定的是一个01回文串
Alice和Bob可以依次进行下面两个操作
1.如果s[i]=0,那么花费1使得s[i]=1
2.如果这个串不是回文串可以选择反转整个字符串，但是如果一个人选择了反转，那么后面那个人不能在下一步操作中也选择反转
Alice先手
如果全为1了，那么游戏结束。此时比较两人花费，谁花的少谁赢。
思路
字符串状态转移图

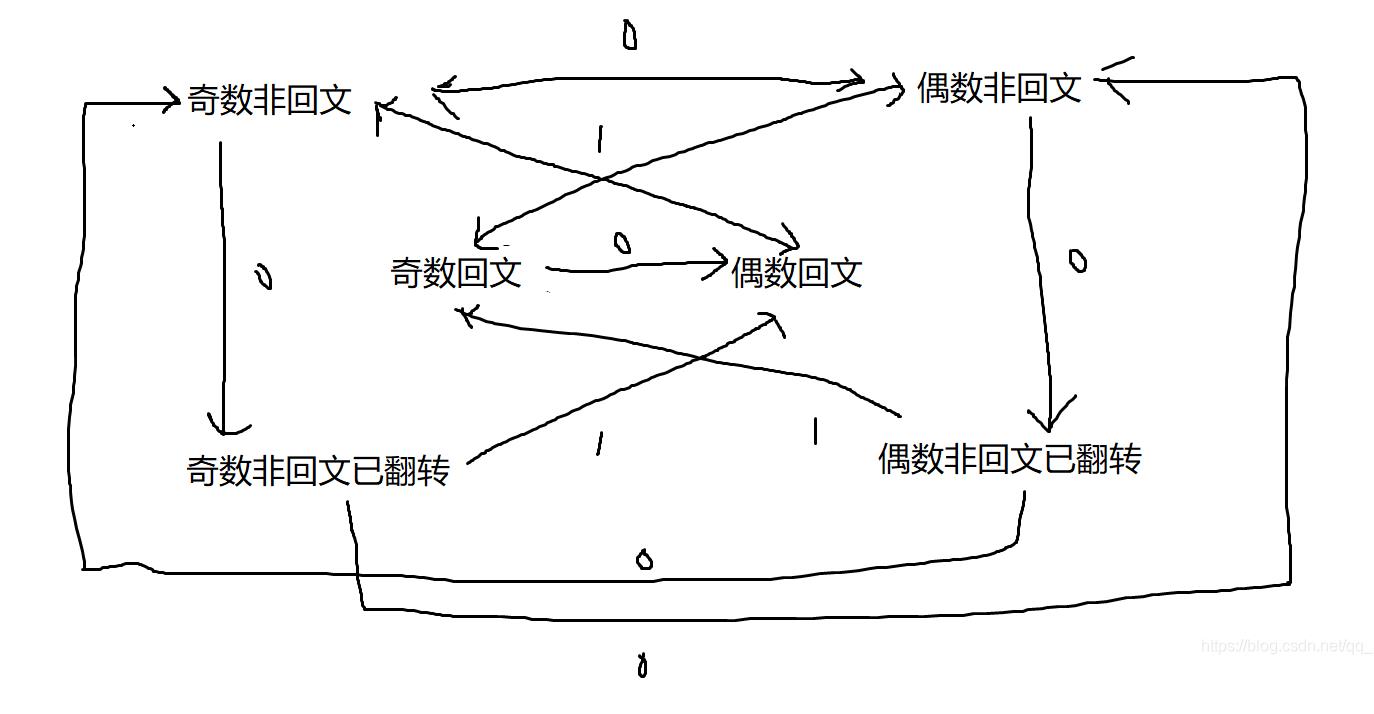
在这里插入图片描述

为了赢得游戏，每个人的最优策略应当是让对手尽可能进入回文状态/非回文已经翻转状态，这样就能迫使对方花费更多，并且如果可以同时从非回文进入已翻转和回文状态，选择翻转减少自己花费
（需要做一些特判<=2的时候）

根据这一规则删除一些不必要的路线
由于这题easy版本开局必是回文的所以只要考虑奇数回文和偶数回文状态即可

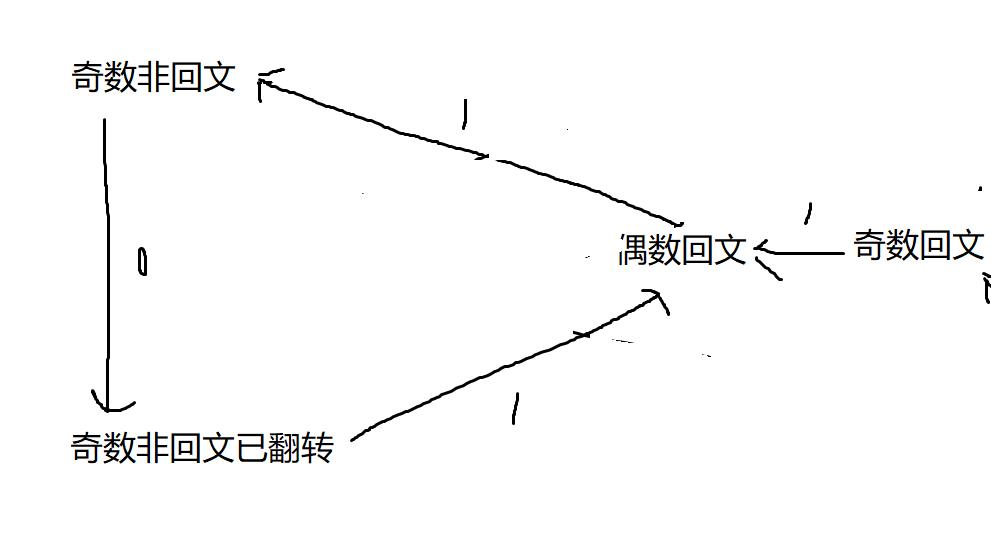
在这里插入图片描述
代码

// Problem: B1. Palindrome Game (easy version)
// Contest: Codeforces - Codeforces Round #721 (Div. 2)
// URL: https://codeforces.com/contest/1527/problem/B1
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// FishingRod

#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY

*/
int T;
void solve(int C)
{
	//NEW DATA CLEAN
	
	//NOTE!!!
	int n;cin>>n;
	string s;cin>>s;
	int cnt=0;
	for(int i=0;i<n;i++)
		if(s[i]=='0')cnt++;
	if(cnt==1)puts("BOB");
	else if(cnt&1)puts("ALICE");
	else puts("BOB");
}

int main()
{
	#ifdef MULINPUT
		scanf("%d",&T);
		for(int i=1;i<=T;i++)solve(i);
	#else
		solve(1);
	#endif
	return 0;
}

B2. Palindrome Game (hard version)

题意:
easy加强版本，区别是开局给的不一定是回文串
思路
细节没处理出来，主要是消路线的时候没考虑清楚有些路是必须走的。后来看了大佬的视频发现不应该这么想的
大佬的解题视频
分别统计对称0的个数和非对称0的个数
如果非对称0的个数是0，那就是easy版本
如果非对称0的个数不是0，那么一开始Alice就可以选择翻转字符串，并且可以一直进行直到BOB把字符串变成回文的，显然ALICE的优势会越来越大。如果最终变为回文的，那么BOB最多可以取得1次的优势，那么局面最多会被拉平，否则仍旧是ALICE胜利。既然ALICE优势会越来越大，那么考虑最开始只有1个非对称，ALICE优势最小的情况，可以发现BOB能够扳回一局实现平局。
代码

// Problem: B2. Palindrome Game (hard version)
// Contest: Codeforces - Codeforces Round #721 (Div. 2)
// URL: https://codeforces.com/contest/1527/problem/B2
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// FishingRod

#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY

*/
int T;
const int N=1e3+10;
char s[N];
void solve(int C)
{
	//NEW DATA CLEAN
	
	//NOTE!!!
	int n;cin>>n;
	cin>>(s+1);
	LL sum=0,summ=0;
	for(int i=1;i<=(n+1)/2;i++)
		if(s[i]!=s[n-i+1])sum++;//非对称0
	for(int i=1;i<=n;i++)
		if(s[i]==s[n-i+1]&&s[i]=='0')summ++;//对称0
	if(sum==0){
		if(summ%2==0||summ==1)puts("BOB");
		else puts("ALICE");
	}
	else{
		if(summ==1){
			if(sum==1)puts("DRAW");//回文对称状态只有1，BOB扳回一局,实现平局
			else puts("ALICE");
		}
		else puts("ALICE");
	}
	
}

int main()
{
	#ifdef MULINPUT
		scanf("%d",&T);
		for(int i=1;i<=T;i++)solve(i);
	#else
		solve(1);
	#endif
	return 0;
}

C. Sequence Pair Weight

题意
定义一个序列的权重为序列中值相同的无序对数量，即 ( i , j ) 并 且 a [ i ] = = a [ j ] (i,j) 并且a[i]==a[j] (i,j)并且a[i]==a[j]
求a所有子段（长度>=2)权重和
思路
对于每一对符合条件的 （ i , j ) （i,j) （i,j)，题目可以给 i ∗ ( n − j + 1 ) i*(n-j+1) i∗(n−j+1)个区间做贡献
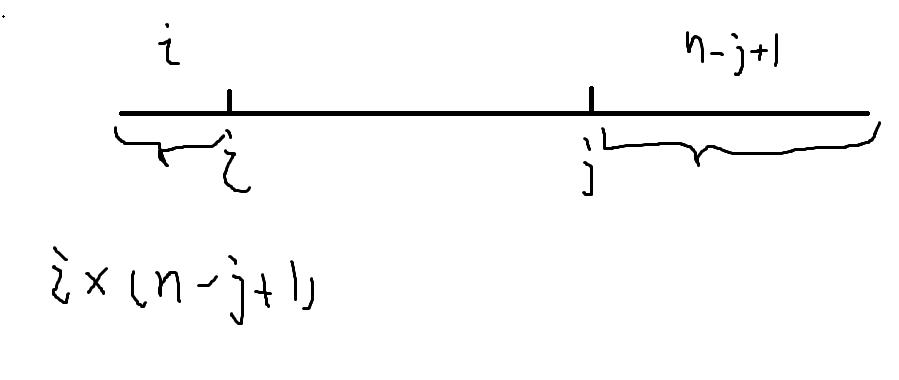
在这里插入图片描述
如果暴力枚举肯定会T，接下来考虑如何优化。
对于同一值a，我们有这些坐标的值等于a
x 1 , x 2 , x 3 , x 4 … … x n x1,x2,x3,x4……x^n x1,x2,x3,x4……xn
我们展开暴力枚举(固定右边的来枚举）
x 1 ∗ ( n − x 2 + 1 ) x1*(n-x2+1) x1∗(n−x2+1)
x 1 ∗ ( n − x 3 + 1 ) x1*(n-x3+1) x1∗(n−x3+1)
x 2 ∗ ( n − x 3 + 1 ) x2*(n-x3+1) x2∗(n−x3+1)
x 1 ∗ ( n − x 4 + 1 ) x1*(n-x4+1) x1∗(n−x4+1)
x 2 ∗ ( n − x 4 + 1 ) x2*(n-x4+1) x2∗(n−x4+1)
x 3 ∗ ( n − x 4 + 1 ) x3*(n-x4+1) x3∗(n−x4+1)
我们可以发现如果右端点固定，后面那一项是相同的，那么可以对前面的进行合并
( x 1 + x 2 + … … + x k − 1 ) ∗ ( n − x k + 1 ) (x1+x2+……+x_{k-1})*(n-x_k+1) (x1+x2+……+xk−1​)∗(n−xk​+1)
对第一项，我们可以做前缀和优化

我们一边输入一边维护值a的前缀和（继续%一下大佬的代码，还是参考B2视频的大佬）
原本想用vector维护，结果写得非常冗余
代码

// Problem: C. Sequence Pair Weight
// Contest: Codeforces - Codeforces Round #721 (Div. 2)
// URL: https://codeforces.com/contest/1527/problem/C
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// FishingRod

#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY

*/
int T;
const int N=1E5+10;
LL a[N];

void solve(int C)
{
	//NEW DATA CLEAN
	map<LL,LL>mp;//mp维护前缀和
	//NOTE!!!
	int n;cin>>n;
	LL sum=0;
	for(int i=1;i<=n;i++){
		LL x;cin>>x;
		if(!mp.count(x)){
			mp[x]+=i;
		}
		else{
			sum+=mp[x]*(n-i+1);//贡献
			mp[x]+=i;
		}
	}
	cout<<sum<<endl;
	
}

int main()
{
	#ifdef MULINPUT
		scanf("%d",&T);
		for(int i=1;i<=T;i++)solve(i);
	#else
		solve(1);
	#endif
	return 0;
}

反思

A：

对于区间答案相同的，主要看这几个方面找规律
先单独看
左端点/右端点变换规律
区间长度变化规律
答案变化规律

数字敏感度
1，3，5，7，15，31
2 n − 1 2^n-1 2n−1

B:

博弈游戏通常考虑
怎么让对面处于不利局面，让自己处于有利局面

C:

对于有easy和hard版本的题目，可以考虑先单独把easy版本情况分开

D:

对所有子区间/子段求点对贡献和，可以考虑点对端点被包含在哪些区间里，然后考虑单个点对可以对多少个区间做贡献。
暴力枚举固定某一端点展开，合并同类项可以考虑前缀和做优化
如果要维护到某一位置，某一个值的前缀和，可以考虑用map来维护

以上是关于解题报告CF DIV2 #ROUND 721 A~C的主要内容，如果未能解决你的问题，请参考以下文章

CF Round #600 (Div 2) 解题报告（A~E）

Codeforces Round #599 Div2解题报告A-D

解题报告CF EDU #ROUND 110 A~C

解题报告CF DIV3 #ROUND 734 A~D1

解题报告CF EDU #ROUND 109A~D （C待补）

Codeforces Round #721 (Rated for Div2)