解题报告CF EDU #ROUND 109A~D (C待补)
Posted 鱼竿钓鱼干
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了解题报告CF EDU #ROUND 109A~D (C待补)相关的知识,希望对你有一定的参考价值。
【解题报告】CF EDU #ROUND 109A~D
比赛评价:
19分钟速杀了AB两题,算是新突破?然后就罚坐卡题,C看了一遍是一道模拟转战D,写了半天贪心结果WA7暴毙。
排名1800+压线进2000

A. Potion-making
题意
每次可以加一次水或者魔法,问最少多少次水和魔法的比例达到要求的百分比
思路
100/gcd(n,100)即可
代码
// Problem: A. Potion-making
// Contest: Codeforces - Educational Codeforces Round 109 (Rated for Div. 2)
// URL: https://codeforces.com/contest/1525/problem/A
// Memory Limit: 256 MB
// Time Limit: 1000 ms
// FishingRod
#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY
*/
int T;
void solve(int C)
{
//NEW DATA CLEAN
//NOTE!!!
int n;cin>>n;
int g=__gcd(n,100);
cout<<100/g<<endl;
}
int main()
{
#ifdef MULINPUT
scanf("%d",&T);
for(int i=1;i<=T;i++)solve(i);
#else
solve(1);
#endif
return 0;
}
B. Permutation Sort
题意
给你一个全排列,你可以选择l,r区间并其中的数重新排列,但是不能一次性全选,问最多弄几次使得数组升序
思路
0
次
,
已
经
升
序
0次,已经升序
0次,已经升序
1
次
,
a
[
1
]
=
=
1
∣
∣
a
[
n
]
=
=
n
1次,a[1]==1||a[n]==n
1次,a[1]==1∣∣a[n]==n
3
次
,
a
[
n
]
=
=
1
&
&
a
[
1
]
=
=
n
3次,a[n]==1 \\&\\& a[1]==n
3次,a[n]==1&&a[1]==n
2
次
,
其
他
情
况
2次,其他情况
2次,其他情况
代码
// Problem: B. Permutation Sort
// Contest: Codeforces - Educational Codeforces Round 109 (Rated for Div. 2)
// URL: https://codeforces.com/contest/1525/problem/B
// Memory Limit: 256 MB
// Time Limit: 2000 ms
// FishingRod
#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
#define MULINPUT
/*DATA & KEY
*/
int T;
const int N=55;
int a[N];
void solve(int C)
{
//NEW DATA CLEAN
//NOTE!!!
int n;cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
bool flag=1;
for(int i=1;i<n;i++)
if(a[i]>=a[i+1])
{
flag=0;
break;
}
if(flag)cout<<0<<endl;
else
{
if(a[1]==1||a[n]==n)cout<<1<<endl;
else
{
if(a[1]==n&&a[n]==1)cout<<3<<endl;
else cout<<2<<endl;
}
}
}
int main()
{
#ifdef MULINPUT
scanf("%d",&T);
for(int i=1;i<=T;i++)solve(i);
#else
solve(1);
#endif
return 0;
}
C. Robot Collisions

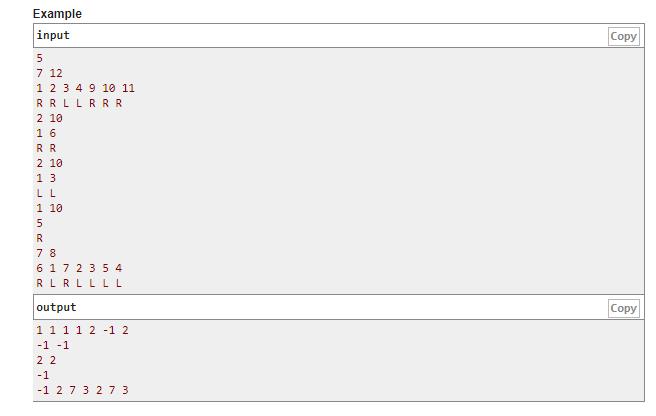
题意
数据结构+模拟+思维,实现不能,思维不能(待补)
思路
首先考虑没有反射的情况,可以发现奇数坐标的和偶数坐标的是永远不可能相撞的,所以我们可以尝试奇数坐标的和偶数坐标的分开考虑。
如果机器人走的方向相对,且同奇偶,那么他们会相撞,消耗的时间为两点距离的一半。可以发现这和栈很类似,最右边或者的机器人和新遍历到的机器人如果方向相反那就会互相抵消。
如果一个机器人向左检查一下栈是否为空,否则的抵消;向右走直接加入栈
如果有反射墙
以堆栈为空向左走为例,我们可以反射它走到墙的距离,我们可以说,他是从-x开始向右走的,因为本来它的右边没有机器,所以换个说法没啥影响。
但是堆栈中最后的机器人(同一方向的)也是不一样的。碰到右边墙反射,他们会依次配对碰撞,第一个和第二个,第三个和第四个。同样的,我们可以m+(m-x)来做坐标反射
代码
就算看了题解也写不出代码的屑是我了,先码了
在这里插入代码片
D. Armchairs

题意
给n个椅子,有的位置上坐了人,有的没有,每个人移动到另一个位置上需要花费
a
b
s
(
i
−
j
)
abs(i-j)
abs(i−j)。问:最少花费多少,让每个人不在原来位置上。
思路
原本想贪心,动态维护查询距离最近的点,然后发现WA7。
赛后大佬发了几道相似题,貌似要用前缀和优化的DP。
不过写贪心的过程中有几点还是需要记录的。
set不怎么支持下标操作,所以如果要用下标相关的信息最好不要用set。
实际上是老鼠进洞模型的DP,可以参考一下这几个博客(主要第一个的)
贪心相关/模拟网络流、费用流细节梳理/模板(贪心,模拟费用流,栈)
老鼠进洞模型
定
义
f
[
i
]
[
j
]
定义f[i][j]
定义f[i][j]到第i个洞位置,已经有j个老鼠进洞了
状态转移:第j个老鼠进第i个洞和第j个老鼠不进第i个洞两种状态转移路径
f
[
i
]
[
j
]
=
m
i
n
(
f
[
i
]
[
j
]
,
f
[
i
−
1
]
[
j
]
)
;
f[i][j]=min(f[i][j],f[i-1][j]);
f[i][j]=min(f[i][j],f[i−1][j]);
f
[
i
]
[
j
]
=
m
i
n
(
f
[
i
]
[
j
]
,
f
[
i
−
1
]
[
j
−
1
]
)
;
f[i][j]=min(f[i][j],f[i-1][j-1]);
f[i][j]=min(f[i][j],f[i−1][j−1]);
初
始
f
[
i
]
[
0
]
=
0
,
其
他
0
x
3
f
用
m
e
m
s
e
t
赋
值
即
可
初始f[i][0]=0,其他0x3f用 memset赋值即可
初始f[i][0]=0,其他0x3f用memset赋值即可
目
标
f
[
c
n
t
h
o
l
e
]
[
c
n
t
m
o
u
s
e
]
目标f [cnt_{hole}][cnt_{mouse}]
目标f[cnthole][cntmouse]
代码
贪心没过的代码
// Problem: D. Armchairs
// Contest: Codeforces - Educational Codeforces Round 109 (Rated for Div. 2)
// URL: https://codeforces.com/contest/1525/problem/D
// Memory Limit: 512 MB
// Time Limit: 2000 ms
// FishingRod
#include<bits/stdc++.h>
using namespace std;
#define endl "\\n"
typedef long long LL;
typedef pair<int,int> PII;
//#define MULINPUT
/*DATA & KEY
*/
int T;
const int N=5005;
bool a[N];
void solve(int C)
{
//NEW DATA CLEAN
//NOTE!!!
int n;cin>>n;
vector<int>v,va,vb;
for(int i=0;i<n;i++)
{
cin>>a[i];
if(a[i]==0)va.push_back(i),vb.push_back(-i);
else v.push_back(i);
}
sort(va.begin(),va.end());
sort(vb.begin(),vb.end());
LL ans=0;
for(int i=0;i<v.size();i++)
{
int pos=v[i];
auto ita=lower_bound(va.begin(),va.end(),pos);
auto itb=lower_bound(vb.begin(),vb.end(),-pos);
int dis=1e9+7;
vector<int>::iterator del;
if(itb!=vb.end())
{
int tmp=abs(itb-vb.begin()-pos);
if(dis>tmp)
{
dis=tmp;
del=itb;
}
}
if(ita!=va.end())
{
int tmp=abs(ita-va.begin()-pos);
if(dis>tmp)
{
dis=tmp;
del=ita;
}
}
int val1=abs(*del),val2=-val1;
//cout<<val1<<endl;
va.erase(lower_bound(va.begin(),va.end(),val1));
vb.erase(lower_bound(vb.begin(),vb.end(),val2));
ans+=abs(pos-val1);
}
cout<<ans<<endl;
}
int main()
{
#ifdef MULINPUT
scanf("%d",&T);
for(int i=1;i<=T;i++)solve(i);
#else
solve(1);
#endif
return 0;
}
AC代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=5e3+10;
bool a[N];
LL hole[N],mouse[N];
LL f[N][N];//f[i][j]前i个洞,匹配了j个老鼠
//第j个老鼠进第i个洞,第j个老鼠不进第i个洞
int n,cnt_hole,cnt_mouse;
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i])mouse[++cnt_mouse]=i;
else hole[++cnt_hole]=i;
}
memset(f,0x3f,sizeof f);
for(int i=0;i<=cnt_hole;i++)f[i][0]=0;
for(int i=1;i<=cnt_hole;i++)
{
for(int j=1;j<=cnt_mouse;j++)
{
f[i][j]=min(f[i][j],f[i-1][j]);
f[i][j]=min(f[i][j],f[i-1][j-1]+abs(hole[i]-mouse[j]));
}
}
cout<<f[cnt_hole][cnt_mouse]<<'\\n';
return 0;
}
反思
A:
比例可以联想到gcd
B:
考虑操作区间能否全覆盖,一般这类题目数量都是有限的,分类讨论即可
C:(待补)
奇偶坐标分开考虑
坐标反射技巧:x+(m-x)
D:
老鼠进洞模型DP
定
义
f
[
i
]
[
j
]
定义f[i][j]
定义f[i][j]到第i个洞位置,已经有j个老鼠进洞了
状态转移:第j个老鼠进第i个洞和第j个老鼠不进第i个洞两种状态转移路径
积累经验:可以把匹配数作为DP参数,到第i个位置匹配了j个,其实还是背包吧。
以上是关于解题报告CF EDU #ROUND 109A~D (C待补)的主要内容,如果未能解决你的问题,请参考以下文章