上下双相机定位贴合（原理到应用，halcon源码详解）

Posted 2021-05-21 苏州程序大白

上下双相机定位贴合（原理到应用，halcon源码详解）

一、简介（类型与之前的文章）看你们理解那个文章快

主要讲解上下双相机定位贴合的原理和实现过程，包括各种标定、组合使用及具体的halcon源码实现，适用于的X、Y、Z三轴加一旋转轴系统，如模组组成的多轴系统、Scara四轴机器、六轴机器人（在运行过程中保证几个自由度不动，运行即可）

二、标定介绍

这一小节总结了通用的相机和轴的相对位置模型，并对其标定进行详细讲解

本系统仅使用了九点标定，精度可做到0.05mm

九点标定作用：
A、本质就是仿射变换，一个坐标系转换到另一个坐标系
B、最少三个不同线的点，九点标定就有一定的拟合 作用,能够减少一部分由于畸变带来的误差
（大家可以了解一下透视变换、仿射变换、相似变换区别和相机镜头畸变）

核心Halcon算子：vector_to_hom_mat2d

1、标定模型A：相机固定（夹具不旋转）

夹具夹取产品或者标定块，选取一个特征，开始进行标定
X轴、Y轴移动一个位置，记录轴的物理坐标：（Qx1,Qy1）
提取图像中对应特征点，图像像素坐标:（Px1,Py1）
…
运动第N位置，记录下点位轴轴坐标（QxN,QyN），t提取像素坐标：（PxN,PyN）
…
一般9点、16点，特征均匀分布在图像的各个位置即可
上面过程在后面就省略讲解。
halcon算子计算：
把上面记录的点转化成halcon的使用的方式，如下：

Px:=[1,2,3]
Py:=[1,2,3]
Qx:=[3,9,12]
Qy:=[3,9,12]
**九点标定使用（仿射变换，最少三个点），不能消除镜头和相机畸变
vector_to_hom_mat2d (Px, Py, Qx , Qy, HomMat2D)

HomMat2D就是得到矩阵

2、标定模型B：相机移动（不旋转）

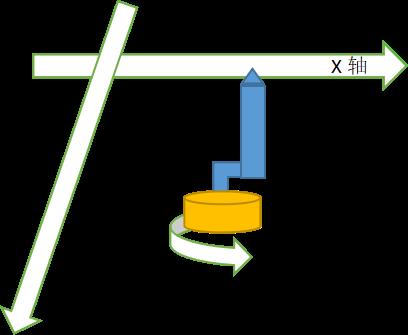
相机固定到X或者Y轴上，不能旋转，这种是大部分设备的移动相机的模式，黄色部分是可旋转的、当时很多设备这黄色部分是包含Z轴或者上下放料气缸。

标定时，把标定特征的产品或者标定块放在相机下方位置固定不动
移动相机（即移动轴），每走一个点，记录下点位轴轴坐标（QxN,QyN），提取像素坐标：（PxN,PyN）
halcon算子计算：
把上面记录的点转化成halcon的使用的方式，如下：

Px:=[1,2,3]
Py:=[1,2,3]
Qx:=[3,9,12]
Qy:=[3,9,12]
**九点标定使用（仿射变换）
vector_to_hom_mat2d (Px, Py, Qx , Qy, HomMat2D)

HomMat2D就是得到矩阵，注意虽然计算过程和模型A一模一样，但是矩阵的使用是不相同，后面会有说明

3、标定模型C：相机固定（夹具旋转）

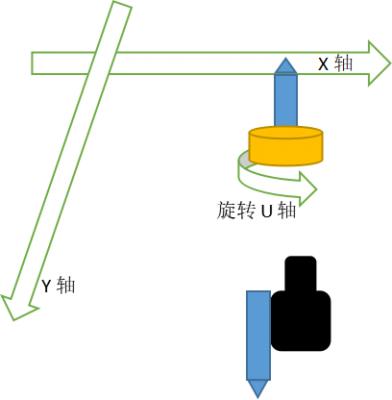
首先实际固定相机的项目，基本上夹具都是可以旋转的，因为我们去夹取的产品肯定有角度偏差，然后通过下方固定相机的拍照，补偿贴合，这也是固定相机意义所在。

所以标定模型A只能补偿Dx、Dy（X轴、Y轴偏差），适用的实际项目情况还是比较特殊的；当前模型需要补偿出角度，但是这个匹配找到产品的角度并不是旋转一下这个角度就好，这会产生一下偏差，这也新手迷惑，或者经常面试问的一个问题，只有了解这个问题定位才算入门。

1. 基本的补偿流程

首先为大家讲一个整体的补偿过程，是怎样产生补偿的，旋转补偿和平移补偿的区别。
放大模型如下:

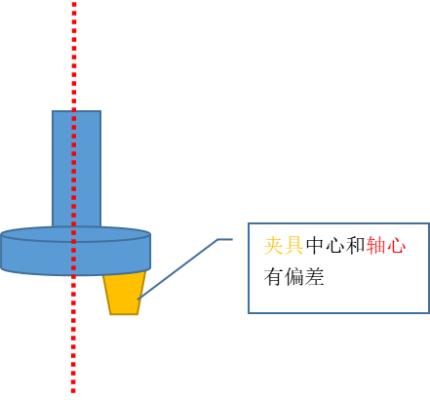
这是一个放大的模型，轴心和夹具中心不重合，就算我们的夹具中心和旋转轴中心是重合，但是我们夹取或者吸取产品也不能保证产品的中心和旋转中心重合，所以结论：涉及旋转必须进行旋转标定，不然每次贴合总会带有旋转产生的误差。

下面分析这个旋转到底是怎样带来误差的，也就是我们旋转标定到底在计算什么东西。
这一部分也同时解释怎样去补偿这个旋转误差。

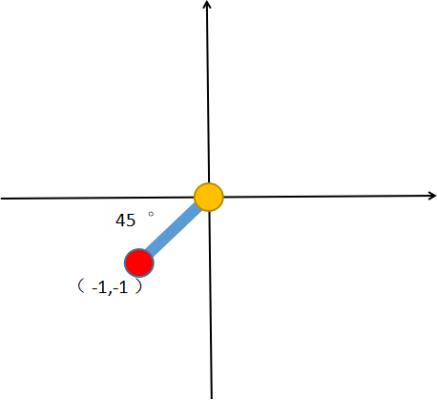
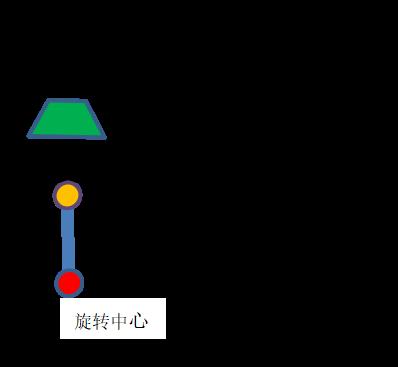
上图的放大模型从下往上看，简化模型在坐标系中，一定搞清楚这里，不然后面旋转起来就没办法理解了

红色圆圈：旋转轴中心
黄色圆圈：夹具中心，这个夹具肯定很大，这里代表其中心位置，在后面计算中没有意义
连线：表示刚性连接（就是两者固定在一起的）

项目中，我们先抓一个产品训练模板，就是模板位置，如下图:

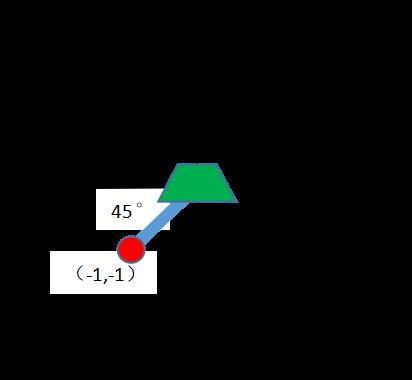
梯形绿色部分：抓取的基准位置产品

模板位置和夹具中心重合，夹具的中心没有实际意义，因为夹具只要把产品抓取进行，我们匹配得到的点位数据是产品的位置，九点标定也是标定特征的数据，和夹具中心没有任何关系，我们直接把模板位置的产品中心当做夹具中心也行。

实际项目中，训练好后，我们就会手动移动轴或者机械手到要放的位置，这就是示教一个标准放置位置M1（x,y,u）（x/y轴坐标值，旋转轴U轴值，后面会用到，记住），然后就是抓取产品拍照，补偿贴合。

所以当前模板产品位置的偏差(0,0,0)

当我们的抓取的一个待放的产品时，它此时的位置可能和我们示教产品的位置不同，这里相当于匹配中心，偏移了（1,1,），旋转了45度，如下图：

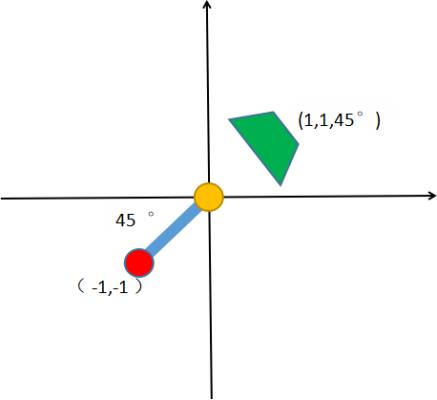
同时注意产品是夹具抓取的，所以旋转轴、夹具、产品是一体，旋转和平移都是一体进行的。

讲到这里，我们很多时候可能开始在这幅上纠结了，想怎么去补偿、旋转等等，试了半天，发现补偿还是不对，最后发现不知道怎会搞了，蒙了，我在哪里，我是谁？？
这里我就要给大家一个定位的这种问题的通用的思路，让人不至于最后懵掉，说到这里，你们难道不点个赞，收藏一下，打赏一下？？

第一步，首先明确我们的目标，就是我们到底在做啥，抓这个产品放到我们的目标问题，所以我们不要在上面图的位置分析。

第二步，假设我们上面的产品没有偏差，直接把产品移动到我们的目标位置：标准放置位置M1（x,y,u），放下产品

第三步，确定我们的看看位置到底是怎样偏差的，然后就知道我们该怎样旋转平移了。

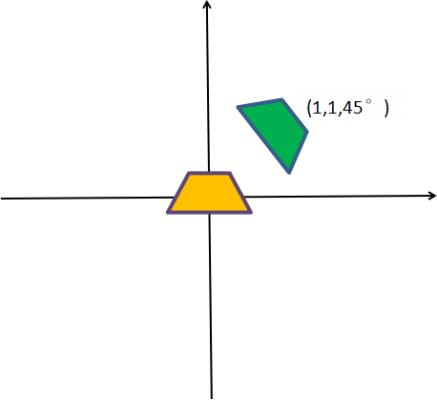
第四步，最后推理出补偿，看见上面图，大家可能感觉很简单了，黄色表示标准位置贴的产品，绿色表示当前产品位置，但是一定要明确上面的图是在我们产品放置位置俯视产生的，所以这个补偿（Dx,Dy,Du）只要直接叠加到M1（x,y,u）上，即得到我们最终的运动位置M2（x+Dx,y+Dy,u+Du），轴或者机器人直接运动到这个位置，放下产品即可。

第五步，计算这个偏差补偿（Dx,Dy,Du），这是我们回到抓取产品的拍照位置，如下图：

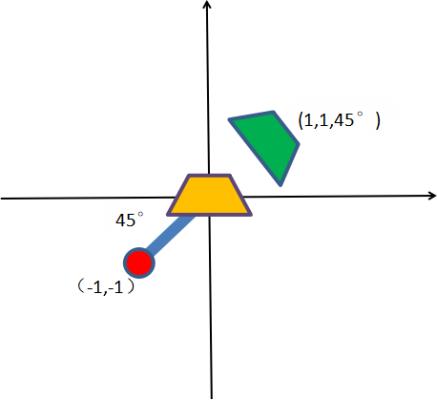
是不是位置和上面一张在产品位置放置点的一模一样，所以直接在这里计算，就可以计算这个偏差。

同时我这么强调产品放置位置和拍照位置，除了让大家了解一个正常定位的补偿流程和思路外，就是得出一个结论：固定的下相机（仅仅这种模型的相机），它作用是通过计算最后得一个偏差，而不是要去计算一些绝对位置；

而绝对贴合的位置是由其他相机或者示教等等产生的；合在一起就组成一个完成补偿。

现在可以回到正题，这个旋转到是怎样产生误差的。

我们只要绿色产品位置移动到黄色位置即可，流程如下：
第一步：移动产品产生的偏差（1,1）：

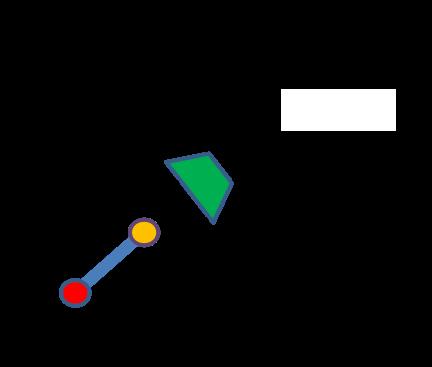
红色旋转中心坐标就变成了(-2,-2)，绿色产品中心（0,0）
第二步：旋转角度45°，一定记住旋转中心在红色圆圈

因为绿色产品中和旋转中心的距离2√2 ,绿色产品中心位置：（-2，2√2-2）
所以可以看出，经过平移和旋转并不能把产品移动到目标位置，发现还差一个偏差（-2，2√2-2）（就是旋转后坐标减去旋转前坐标），这样解决前面的疑惑仅直接旋转获得的角度不正确，会出现一个偏差。

这里点位和角度都很特殊，后面会讲通用的角度位置偏差怎么通过Halcon算子计算。

同时，一定要注意在我们计算这个偏差的时候，我们用到了旋转中心的坐标；但是非常遗憾的问题，我们在做九点校正的时候（根据标定模型A），标定的基准是标定特征的中心，而不是旋转中心，实际项目中我们夹具抓取标定块进行标定，根本做不到把旋转中心和标定特征的中心重合，所以我们就需要通过旋转标定找到旋转中心并消除它。

不容易啊，终于回归本部分的正题了，开始标定了。

此模式：相机固定，夹具旋转，忘记了的看看上面模型图片。

2) 、首先九点标定

首先夹具旋转位置选择，一定要注意因为夹具是可以旋转的，所以当我们夹住产品开始标定时，我们选取那个角度就行标定呢？

这个角度要选好，因为，这就是我们抓取拍照或者飞拍的时候也需要保持这个角度姿态，如果不是这个角度，需要重新经过一个计算转换回去才行，这里需要大神来帮忙补充一下；因为我现在遇到的项目暂时还没有要求这个，因为只要旋转好的姿态标定就可以满足。

基本要求：
A、角度肯定能到拍照位置能拍照，别选一个角度导致轴或者机器人最后根本就走不到拍照点
B、选择这个角度姿态，有利于我们在定点旋转时，能够旋转更大的角度，因为旋转标定找圆心，其实就是定点旋转我们的标定特征，然后拟合找圆心，很明显点分布的角度越大，精度越高（没有做过旋转的，不理解没关系，后面讲解，到时回来看看就知道怎么回事了）；200°旋转效果已经非常好了，很多时候因为视野和机构问题，能到达90°就已经可以了；

九点标定过程：
当这个旋转角度确定后，九点标定就变成了了标准模型A，过程就不详细讲了，这时就得到了一个矩阵：HomMat2D。

我们前面提到过这个矩阵其实就是两个坐标系转换关系，这里是指下相机的图片上像素坐标和标定特征中心的物理坐标的关系，但是上面我们知道了，我们需要的是下相机的图片上像素坐标和旋转中心的物理坐标的关系，所以下面进行旋转标定。
注：那如果遇到项目的旋转臂很长，视野不够大，旋转几度都没有，这种项目有吗？肯定有啊。如果你们谁遇到了，由于读到这里受启发，是不是回来帮忙点个赞呢。方法就是旋转后，标定特征离开视野，只需要平移到视野中，提取特征计算后要减去这个平移值在拟合。

还有一个小诀窍，如果精度不是太高，两个点就行，一个点记录，然后直接转180度，再记录，直接就是直径了，两个点计算物理点相加除以2就是圆心，具体你们自己看着办吧，是不是感觉处处是惊喜啊，又学到了一招。

网上搜索相机标定，一大堆像素坐标系、图像坐标系、相机坐标系、世界坐标系，还有手眼标定里面的各个坐标系都不要去考虑，九点标定就是相机得到的图像像素坐标与轴或者机器人的X、Y物理坐标的关系，就是两个平面坐标的转换，不要去复杂话你的系统考虑中间问题。

所以六轴机器人来做九点标定，第一步应该是建立与工作平面平行的平面，然后再这个平面移动做九点标定，至于这个机器人的这个新坐标系怎么建立就找搞机器人的就行；当然如果要求不高，忽略。

3) 旋转标定

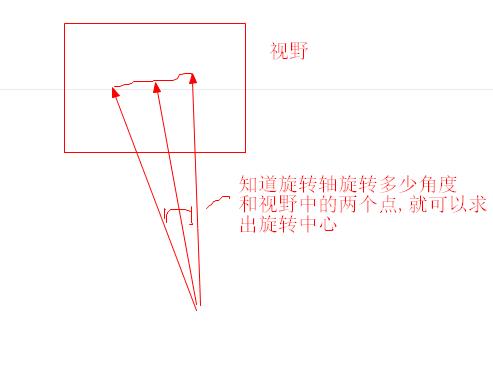
首先选择一个定点，记录下点物理坐标P1（x,y），然后如下图绕着红色的旋转中心旋转，黄色表示标定的特征中心，灰色表示相机的图像，并且可以从图像看出，左边的旋转角度可能旋转90-120之间，其他位置已经跑出图像外了，而右边的旋转半径短（标定特征中心和旋转中心距离，实际项目机械结构决定的），视野大，所以旋转大于200度，保证特征在视野内。

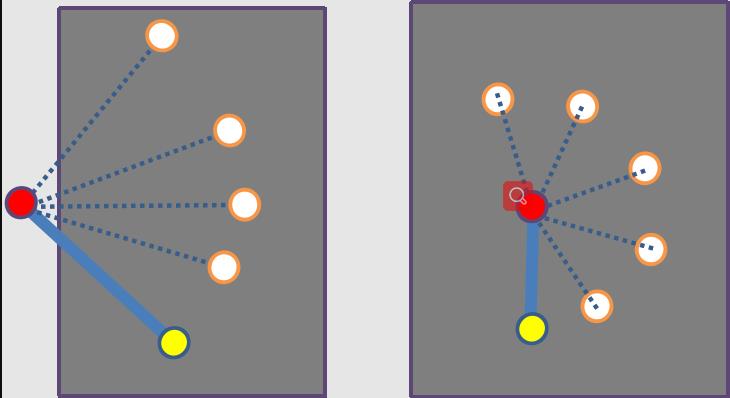
再次强调这个旋转的前提，在定点P1（x,y）不变的位置进行旋转，这个点是“初始角度”的标定特征中心的坐标，而不是旋转中心的坐标。
计算过程如下：
记录第一个点物理点P1（x,y），提取特征中心的像素为(Prx1,Pry1）
旋转一个小角度，
记录第二个点物理点P1（x,y），提取特征中心的像素为(Prx2,Pry2）
咦，怎么物理点都没变呢都是P1呢，肯定啊，X，Y轴都没有动，X/Y坐标肯定不变啊；既然不变为啥要提他呢，因为我知道很多人一转起来又懵逼了，又不清楚自己在哪里了；一定搞清楚什么在变动，什么不变。
…
旋转第N个点物理点P1（x,y），提取特征中心的像素为(PrxN,PryN）
…
具体多少个点，旋转16-20个点完全够了。

现在已知的条件：定点物理点P1（x,y），一系列像素坐标（PrxN,PryN），还是有我们前面九点标定矩阵HomMat2D（不要忘了）。
求取？？
一团乱，求取啥呢？一定不要忘了我们的初衷，得到旋转中心坐标和图像的像素坐标的关系，本质上呢：就是一个矩阵：HomMat2D_C1（模型C矩阵）
求取：HomMat2D_C1

第一步，拟合点计算：
*九点标定的矩阵
HomMat2D:=[0.0202215, 3.43298e-005, -27.1543, 3.20314e-005, -0.0202298, 75.8988]
*旋转点集的像素坐标，例如如下
Prx:=[0,1,2,3,4,5,6]
Pry:=[0,1,2,3,4,5,6]

for Index := 0 to |Prx|-1 by 1
   *通过矩阵转换一个点到另一点的算子
   affine_trans_point_2d (HomMat2D, Prx[Index], Pry[Index], Qx, Qy)
   Qrx[Index]:=Qx
   Qry[Index]:=Qy
Endfor
最核心的一个算子：affine_trans_point_2d，就是一个矩阵转换点。
就是把一系列的像素点for循环转换为物理坐标点，用来拟合圆，
上面就算已经得到我们的物理的拟合点Qrx, Qry

第二步，拟合圆：
*拟合圆
*先生成轮廓
gen_contour_polygon_xld (Contour, Qry, Qrx)
*轮廓拟合圆，算法要选择'geotukey'，自己看说明文档
fit_circle_contour_xld (Contour, 'geotukey', -1, 0, 0, 3, 2, Row_C, Column_C, Radius_C, StartPhi, EndPhi, PointOrder)

拟合圆不细讲，网上都有，得到我们的圆心（Column_C,Row_C）（注意这里X，Y坐标和行、列坐标区别）,半径：Radius_C

完了吗？肯定没有啊，我们要明白我们的初衷，求旋转中心坐标和图像的像素坐标的关系：HomMat2D_C1（模型C矩阵），现在还不是呢

第三步，计算偏差：
既然已经知道旋转中心坐标，那我们就可以求出标定中心和旋转中心的偏差：
还记的上面的我们是在P1（x,y）做的定点旋转，同时也是“初始角度”的标定特征中心的坐标
halocn计算偏差：
*定点P1
x:=1
y:=1
Dx_C:=Column_C-x
Dy_C:=Row_C-y

这就是一个固定偏差值，代表是标定点特征中心和旋转中心的偏差；
同时一定要理解，这个偏差也是九点标定的旋转轴的角度的姿态计算得到；
如果我们旋转轴的角度发生改变，这个偏差是会变的；

如果项目的补偿每次都有偏差。你查查你的项目，遇到过这种情况吗，补偿不稳定。（因为旋转中心标定不准导致的）

完成了吗？可以说完成，也可以说没有完成。

我们得到了Dx_C , Dy_C，HomMat2D，已经可以用了，你们可以去看看你们的项目，很多都这样就是了，我开始也这样保存到本地就完了，后来我才发现还有优化的空间，让我们的计算更加优雅。

同时如果你们的定位项目中出现sin,cos等待三角函数时，那肯定可以优化，因为标定都是坐标点（x，y）的关系，点到点都可以通过矩阵实现，最主要是halcon已经提供这些库，学会用就行。

至于这样怎么样有优化，为什么这样优化必须放在使用这些矩阵的一章来进行分析了。

固定旋转终于讲完了，从简单到复杂一步步来，搞清楚了吗？没搞过的，搞不清楚拿起笔画一画啊，打开halcon17.12，自己模拟一下特殊点验证一下啊，都是高中的一些平面几何知识，你只需要把设备模型抽象出来，halcon数学的算子都有啊，话都说到这里了，如果不动手自己理解，到时只有项目实战试试也行。

如果现在最简单的旋转你不理解一下，到时下面我们开始旋转相机的时候，你会懵逼掉的。

如果搞清楚了，恭喜你，其实大家说的飞拍的项目的单相机补偿，你可以搞起了；至于怎样使用上面三个参数，我相信你通过我上面讲的基本补偿流程，试几次应该就能搞出来。因为飞拍的项目基本都是这种模型。

4. 标定模型D:相机移动（可旋转）

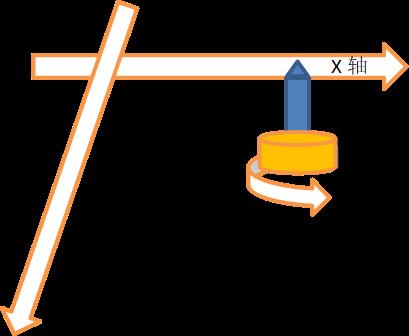
这个模型如上图，黄色部分旋转U轴，上面固定相机，表示相机和我们的夹具一起旋转，为啥会出现这种模式呢，就我个人的遇到的情况，就是因为有Scara机器人安装需求或者限制，导致必须要这样安装如下图：

模型D和模型B就是相机可以旋转，如果我们拍照的时候，保持旋转轴的角度和标定的一致，其实就相当于相机在我们整个过程中是没有旋转的，等同于模型B；
同时我先要说明，如果这个九点标定的角度和拍照时旋转轴的角度不同，计算有哪些变化，我没有是实现过，如果哪位大神实现过，给点提示；后面如果有时间，我也实际测试一下任意角度拍照的变换，到时更新给大家。
实际项目过程中，保持拍照的旋转轴的角度和标定的一致这个很容易实现，首先先选择一个拍照的角度，然后再按照这个角度进行九点标定即可，后面就按照中模式就行讲解。

1) 九点标定

选择一个拍照的姿态，确定旋转轴的角度，然后就开始九点标定，过程和模型B相同。
这里不详解，得到矩阵：HomMat2D

2) 旋转标定

如果只是它当做模型B来使用，不进行旋转标定一样可以使用；在模型B的部分讲得比较简单，这里做一些说明。

上相机到底来干什么的？

这里也回顾一下，我们上面讲的模型C的相机也就是下相机的作用，它是来计算用于贴合或者装配产品的抓取的偏差。

而上相机用来确定被贴或者被放置的产品的位置偏差，就是我们的贴合的目标位置每次都是变动的，这也很好理解，就是当前贴合设备在当前产品贴合了，下一个产品进来（皮带轨道传入或者机器手放入），这个产品的位置和上一次都有一些小的偏差，这样就导致了贴合的目标位置每次有变动，这是就需要我们的上相机先计算目标的贴合位置。

如果是高精度的定位模具来放置目标产品，这是不需要上相机来。

同时一定要理解的是：这里移动相机的九点标定得到的结果是相机的物理坐标与目标位置的像素坐标的关系，因为相机移动，目标位置即贴合位置在相机下方不动的，通过图像的像素坐标计算。
但是我们最终要去贴合的时候，是夹具夹取贴合物品放到目标位置，需要是夹具的位置与 目标位置的关系，但是通过模型B和模型D发现，我们的相机和夹具的位置关系是固定不变的，存在一个固定的机械偏差（Mx,My）。
这里说的夹具位置其实就是指旋转中心，不要因为上面的四轴机器人图，以为我标的夹具位置才是它的中心，一定注意这个夹具是不能旋转的，应该说没有必要，我们四轴机器人的末尾都带有一个旋转轴，通过这个轴实现旋转；模型B中的夹具可能自带旋转，但是本质上两种都一样的，结论就是夹具的中心就是旋转中心。

同时也到这里我们也整理出上下相机贴合的第一张核心补偿关系图：

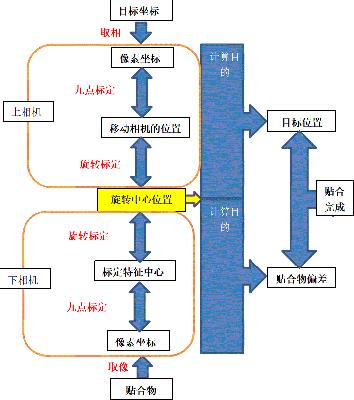
这张图已经包含所有本文章的需要讲解的上下相机定位贴合的标定和补偿的整个思路，非常有利于你理清你的整个思路。突然灵光一闪想到搞这样一张图，花了很多时间的整理这张图。
上面这张图：

主要这张图不是上下对称的，上下相机的标定关系完全不同，请细心看每一个字，整个文章就是按照上面图来讲解的。
A、上下相机的输入不同，下相机：用于贴合的产品；上相机：目标产品的位置

B、最后标定中心的关系以不同：下相机：标定特征中心，上相机：移动相机的物理位置

C、上下相机的标定得到的转换关系（就是我们标定的转换矩阵）不同：下相机：贴合物的像素坐标与旋转中心的关系；上相机：目标贴合位置与旋转中心的关系

D、上下相机关系纽带：就是旋转中心。

E、计算目的不同：下相机：求取的贴合物的偏差；上相机：求取的是目标的绝对位置

F、同时也要注意上相机的如果没有旋转，没有旋转标定，这里的其实就是上文提到的：因为相机和夹具的位置关系是固定不变的，存在一个固定的机械偏差（Mx,My），就是这个偏差值。

通过上面的图，你可以站在一个整体或者更高的角度理解，为什么进行标定及其意义在哪里，同时上下相机补偿的时候你也可以按照这个图中的思路去完成，让你思路更清晰。

模型B的上相机的与旋转中心的固定偏差（Mx,My），在使用过程中，可以直接使用机械图纸中的测量值，当然安装等等误差不可能等于这个理论值，有微小偏差；但是在我们示教贴合第一个产品时，我们会手动示教出一个固定的偏差，这个示教的偏差已经包含了上面的微小偏差，所以可以不用标定这个偏差；
同时也一直有一个疑惑，不进行第一个点示教，直接标定完，贴合出来就是绝对准确位置能实现吗，分析了一下好像是可行的，没有测试过，不过标定好像要标定几个基准并且标定要准，不知道有没有人帮忙解答一下；
如果项目需要标定这个偏差，做一个专用的标定夹具在旋转中心，标定块向下点一个点或者旋转中心对位一个点，记录下机械点，然后移动上相机让这个点在图像中心，这样就计算出这个固定偏差（Mx,My），这里就不详解。

对于本部分模型而言，因为相机可以旋转，所以可以直接通过旋转标定进行计算出固定偏差（Mx,My）。

如下：
在四轴机器人调整到定点P2（x,y）不变的位置进行旋转，选择一个好的角度和位置，这样选择旋转位置前面也讲过，相机下方放置一个固定标定特征，然后旋转轴每次固定角度旋转拍出，旋转拍照。
计算过程如下：
记录第一个点物理点P2（x,y），提取特征中心的像素为(Prx1,Pry1）
旋转一个小角度，
记录第二个点物理点P2（x,y），提取特征中心的像素为(Prx2,Pry2）
…
旋转第N个点物理点P2（x,y），提取特征中心的像素为(PrxN,PryN）
…

现在已知的条件：定点物理点P2（x,y），一系列像素坐标（PrxN,PryN），还是有我们前面九点标定矩阵HomMat2D（不要忘了）。

这些过程都和模型C的旋转一样，只是这个模型的相机在移动。

求取的固定偏差（Mx,My）

Halcon计算如下：
第一步，拟合点计算：
*九点标定的矩阵
HomMat2D:=[0.0202215, 3.43298e-005, -27.1543, 3.20314e-005, -0.0202298, 75.8988]
*旋转点集的像素坐标，例如如下
Prx:=[0,1,2,3,4,5,6]
Pry:=[0,1,2,3,4,5,6]

for Index := 0 to |Prx|-1 by 1
   *通过矩阵转换一个点到另一点的算子
   affine_trans_point_2d (HomMat2D, Prx[Index], Pry[Index], Qx, Qy)
   Qrx[Index]:=Qx
   Qry[Index]:=Qy
Endfor
已经得到我们的物理的拟合点Qrx, Qry

第二步，拟合圆：
*拟合圆
*先生成轮廓
gen_contour_polygon_xld (Contour, Qry, Qrx)
*轮廓拟合圆，算法要选择'geotukey'，自己看说明文档
fit_circle_contour_xld (Contour, 'geotukey', -1, 0, 0, 3, 2, Row_D, Column_D, Radius_D, StartPhi, EndPhi, PointOrder)

拟合圆不细讲，网上都有，得到我们的圆心（Column_D,Row_D）（注意这里X，Y坐标和行、列坐标区别）,半径：Radius_D

Radius_D就是相机到旋转中心距离，拿直尺量一下对比一下，如果相差很离谱那肯定是计算哪里有问题，查找一下问题
验证九点标定是否正确：
计算九点标定后，图像中心的坐标经过矩阵转换得到物理坐标，运动到这个点，计算图像中的标定物体的像素坐标应该是图像中心的坐标，先看看这个是否正确，然后在验证旋转

验证旋转标定是否正确：
图像中心的坐标经过矩阵转换得到物理坐标，然后加上计算的偏差，然后运动到这个点：如果模型C：发现旋转中心在图像中心就是正确的；如果模型D：发现旋转中心在标定特征的正上方就是正确的。

第三步，计算偏差：
既然已经知道旋转中心坐标，那我们就可以求出标定中心和旋转中心的偏差：
还记的上面的我们是在P2（x,y）做的定点旋转
halocn计算偏差：
*定点P2
x:=1
y:=1
Mx:=Column_D-x
My:=Row_D-y

三、上下双相机贴合模型

整个补偿的思路及过程都在第二章的模型D中已经讲过，这里就不再进行分析了。
整体思路：
上相机作用：确定贴合的产品的放置位置
下相机作用：确定抓取或者吸取料的偏差值

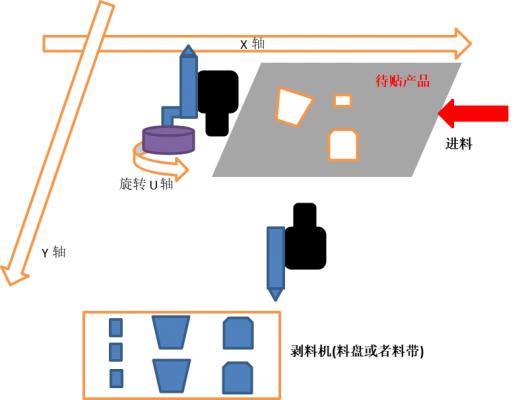
1、贴合模型：模型B + 模型C

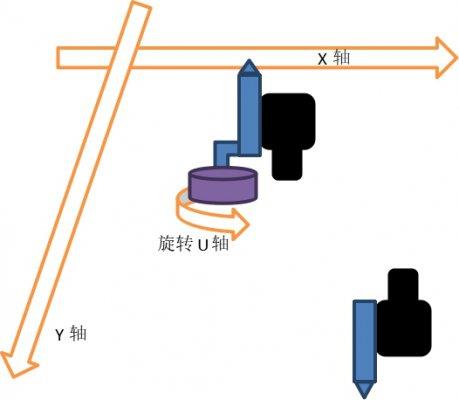
上图是当前贴合项目的主流的模型，了解这种模型整个补偿过程，其他变种模型也基本雷同，上图中的部件组成不进行详细讲解，见上文即可。
工作流程，后面的讲解也按照以下流程进行，如下图：
A、产品进入当前工位（轨道流入或者机器人抓入），如图三个位置需要贴料
B、X.Y轴移动到剥料机位置，抓取料
C、运动到下相机位置拍照，计算偏差
D、X.Y轴运动到贴合位置，加上偏差进行贴料
E、产品离开当前工位，等待下一个产品
当然有些设备，可以先取料下相机拍照计算好偏差，等待产品流入，在上相机拍照后直接贴合，更加实际需求设计流程。

2. 上相机计算贴合位置

产品到位，X、Y轴运动到设置好的拍照点机械点M1（x,y）
上相机拍照，视觉匹配处理得到当前产品像素坐标C1（x,y,u）

回顾一下标定模型B得到的九点标定矩阵，这里定义矩阵为：HomMat2D_B
同时上文还讲到了模型B的上相机的与旋转中心的固定偏差（Mx,My）

通过上面我们就可以计算贴合的位置：
第一步：

大家可能都知道，是求像素转换的坐标：

*九点标定的矩阵

HomMat2D_B:=[0.0202215, 3.43298e-005, -27.1543, 3.20314e-005, -0.0202298, 75.8988]

*当前产品像素坐标C1（x,y,u）,得转换坐标：QC1（x,y）
Xc1:=2.5
Yc1:=2.5
affine_trans_point_2d (HomMat2D_B, Xc1, Yc1, Qxc1, Qyc1)

第二步：
给大家说一个说一个比较隐藏概念：

相机的九点标定都是有位置基准的。

下相机九点因为下相机固定不变，这个基本是不动的，同时下相机拍照时候都是料运动到下相机的视野中，所以下相机九点标定的矩阵直接用就行。

但是对于上相机来说，相机运动的，拍照位置也是变动的，和九点标定位置肯定不同，所以计算出来肯定存在偏差。下面解释一下为什么会有基准：

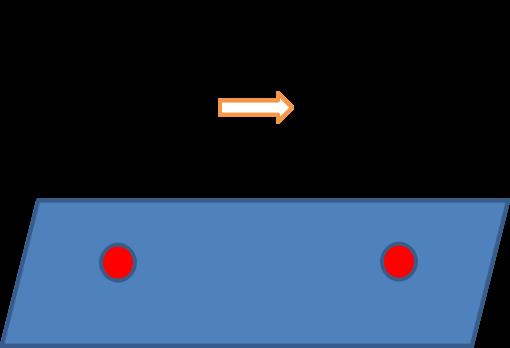
相机在位置1进行拍照，假设在位置1红圆点的正上方，这样像素就是图像中心（Width/2,Height/2,）；
相机运动到位置2，假设也是在位置2红圆点的正上方，这样像素也是（Width/2,Height/2）;
上面两次像素都进过第一步计算，因为变换矩阵都是HomMat2D_B，所以计算出来的物理坐标肯定一样的，但是实际上拍照时两个位置拍照的，所以物理坐标应该是不一样的。
所以这里需要找到九点标定的基准位置，九点标定九个位置，哪个位置是基准？
就是最特殊点，那就是像素坐标的（0,0）点，同时要记住像素中的特殊点都是有物理意义的：
所以第二步的计算过程：
*标定的基准点（0,0）,得转换坐标：Base（x,y）
affine_trans_point_2d (HomMat2D_B, 0, 0, Xbase, Ybase)

第三步
计算当前点Qup(x,y)：
Qxup=Xm1-Xbase-Qxc1-Mx
Qyup=Ym1-Ybase-Qyc1-My
（当前贴合坐标=当前X、Y轴物理坐标-标定基准坐标-当前计算像素坐标-相机与旋转中心偏差）
上面要减去第一步计算的坐标QC1（x,y）坐标，就是相机移动，相对于下面的固定拍照的产品说在图像中是向反方向移动。
同时最可怕的一点如果不知道移动相机计算出来的坐标用减，那永远试不出来正确的补偿。

关注苏州程序大白，持续更新技术分享。谢谢大家支持