机器学习40讲学习笔记17 -几何角度看分类：支持向量机

Posted 2021-05-20 bohu83

一 序

    本文属于极客时间机器学习40讲学习笔记系列。

17 | 几何角度看分类：支持向量机

     一提到支持向量机，大部分人的第一反应都是核技巧，所谓的核技巧（kernel trick）只是支持向量机的一个拓展，通过维度的升高将决策边界从线性推广为非线性。所以对于支持向量机的基本原则的理解与核技巧无关，而是关乎决策边界的生成方式。

                      线性可分数据集的决策边界

如果一个数据集是二维平面上的线性可分数据集，那它的决策边界就是一条简单的直线。可这条能将所有训练数据正确区分的直线是不是唯一的呢？显然像这样的能正确区分数据的直线有无数条。

在这些直线里，哪一条是最好的呢？划分的不好，过于靠近一些训练数据,这些靠近边界的数据受噪声影响误判，距离两侧的数据都比较远，位于不同类别数据正中间的决策边界对样本扰动的容忍度最高，在未知数据上的泛化性能也就最好。

  

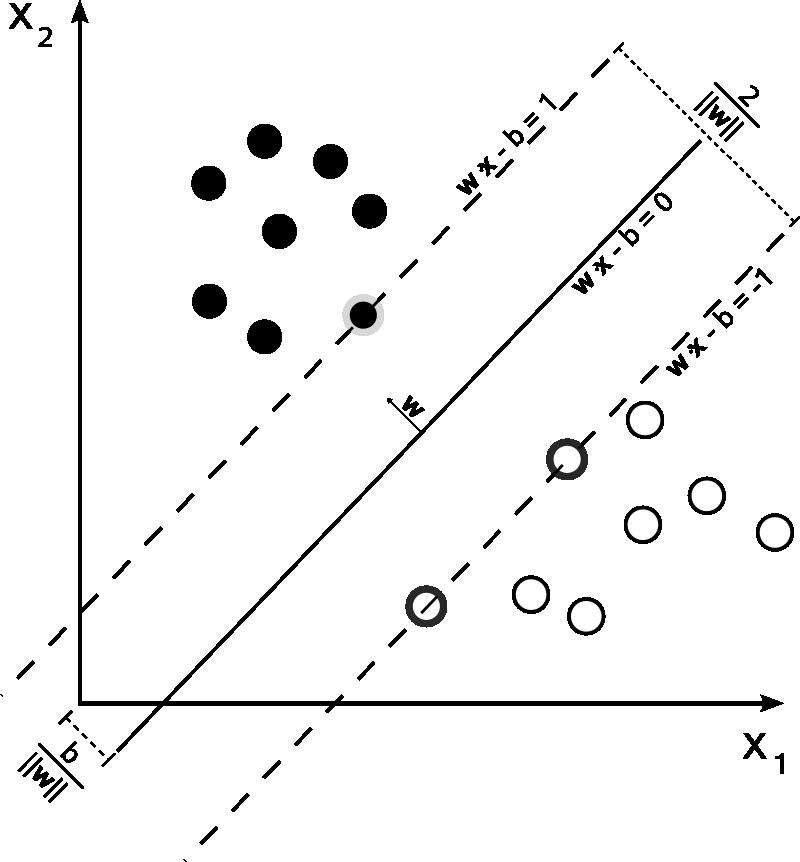
      间隔（margin）是支持向量机的核心概念之一，它是对支持向量到分离超平面的距离度量，可以进一步表示分类的正确性和可信程度。当数据线性可分时，分离超平面有千千万，但几何间隔最大的只有一个。支持向量机的基本思想就是找出能够正确划分数据集并且具有最大几何间隔的分离超平面（maximum-margin hyperplane）。

   约束条件又分为：硬间隔（hard margin），软间隔（soft margin），因为硬约束条件对于异常点效果不一定好，在计算软间隔时，支持向量机利用合页损失函数（hinge loss）来表示分类错误率。合页损失可以看成是对计数表示的分类错误率的近似。因此在软间隔的优化中，也只需要考虑几个异常点对决策边界的影响。这恰恰体现出了支持向量机的思想方法：最终的决策边界仅与少数的支持向量有关，并不会受到大量普通数据的影响。

   训练误差太小并不是好事，这很有可能导致模型过于复杂而出现过拟合。结构风险最小化就是带着抑制过拟合的任务出现的。

除了间隔之外，支持向量机的另一个核心概念是对偶性（duality）。间隔的作用体现在原理上，而对偶性的作用体现在实现上。primal-form的问题比较难以解决因此转换到dual-form。

     在 Python 中实现支持向量机，需要调用 Scikit-learn 库中的 svm 模块，通过其中的 SVC 类来实现分类。要生成线性边界，需要将 SVC 中的 kernel 参数设置为 linear，同时还要将常数项 C 设置为一个接近正无穷的值，以避免正则化的使用。

   这里老师基本上从几何角度来看SVM，之前文哲老师从推导计算角度来讲：https://blog.csdn.net/bohu83/article/details/114198931