机器学习40讲2-学习笔记

Posted 2021-05-14 bohu83

一 序

  本文属于极客时间机器学习40讲学习笔记。

03 学什么与怎么学

   机器学习侧重于将预先设定的准确率等指标最大化，那模式识别就更注重于潜在模式的提取与解释。

什么样的问题才能通过机器学习来解决呢？

首先，问题不能是完全随机的，需要具备一定的模式；其次，问题本身不能通过纯计算的方法解决；再次，有大量的数据可供使用。

机器学习的任务，就是使用数据计算出与目标函数最接近的假设，或者说拟合出最精确的模型 。

输入特征：具体特征（concrete feature）、原始特征（raw feature）和抽象特征（abstract feature），在解决实际问题时，具体特征可以直接使用，原始特征通常需要转换成具体特征，抽象特征就需要根据实际情况加以取舍。

看完了输入特征，再来看看输出结果。根据输出结果的不同，可以将机器学习的方法分成分类算法（classification）、回归算法（regression）和标注算法（tagging）三类。

    如果训练数据中的每组输入都有其对应的输出结果，这类学习任务就是监督学习（supervised learning），对没有输出的数据进行学习则是无监督学习（unsupervised learning）。监督学习适用于预测任务，无监督学习适用于描述任务。    

  学习策略：大部分算法是集中处理所有的数据，也就是一口气对整个数据集进行建模与学习，并得到最佳假设。这种策略被称为批量学习（batch learning），和它相对应的是在线学习（online learning）。在在线学习中，数据是以细水长流的方式一点点使用，算法也会根据数据的不断馈入而动态地更新。

分类：从输入空间、输出空间、数据标签、学习策略等角度可以对机器学习进行分类。

04 计算学习理论 

 本节介绍计算学习的理论，偏抽象些，没看懂。  

     学习的目的不是验证已知，而是探索未知，人类和机器都是如此。对于机器学习来说，如果不能通过算法获得存在于训练集之外的信息，学习任务在这样的问题上就是不可行的。

    在概率论中，有界的独立随机变量的求和结果与求和数学期望的偏离程度存在一个固定的上界，这一关系可以用 Hoeffding 不等式（Hoeffding's Inequality）来表示。

     让模型取得较小的泛化误差可以分成两步：一是让训练误差足够小，二是让泛化误差和训练误差足够接近。正是这种思路催生了机器学习中的“概率近似正确”（Probably Approximately Correct, PAC）学习理论，它是一套用来对机器学习进行数学分析的理论框架。在这个框架下，机器学习利用训练集来选择出的模型很可能（对应名称中的“概率”）具有较低的泛化误差（对应名称中的“近似正确”）

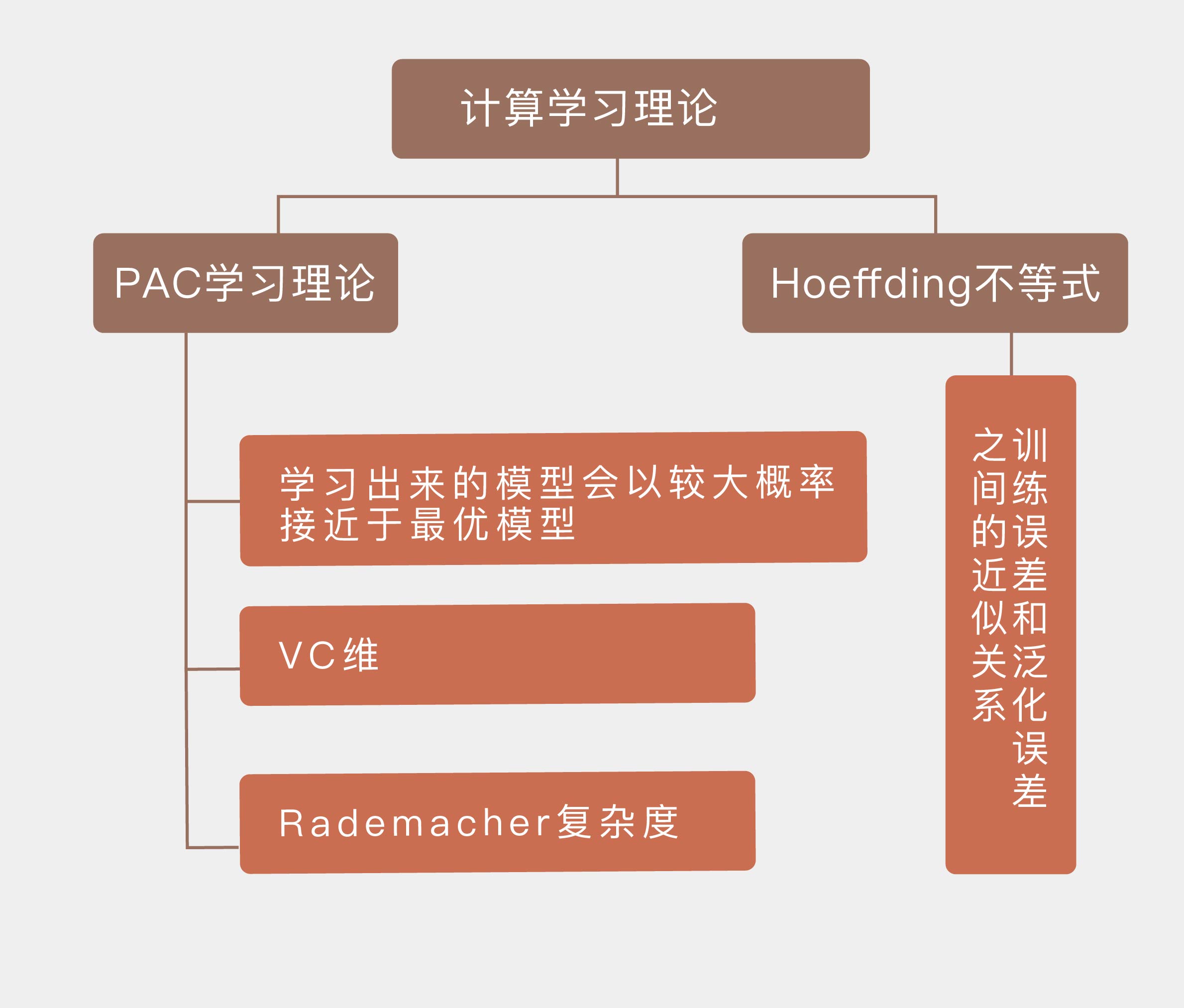
•  Hoeffding 不等式描述了训练误差和泛化误差之间的近似关系；
• PAC 学习理论的核心在于学习出来的模型会以较大概率接近于最优模型；
• 假设空间的 VC 维是对无限假设空间复杂度的度量，体现了复杂性和性能的折中；
• Rademacher 复杂度是结合了先验信息的对函数空间复杂度的度量。

05  模型的分类方式

 机器学习学的是输入和输出之间的映射关系，学到的映射会以模型的形式出现。

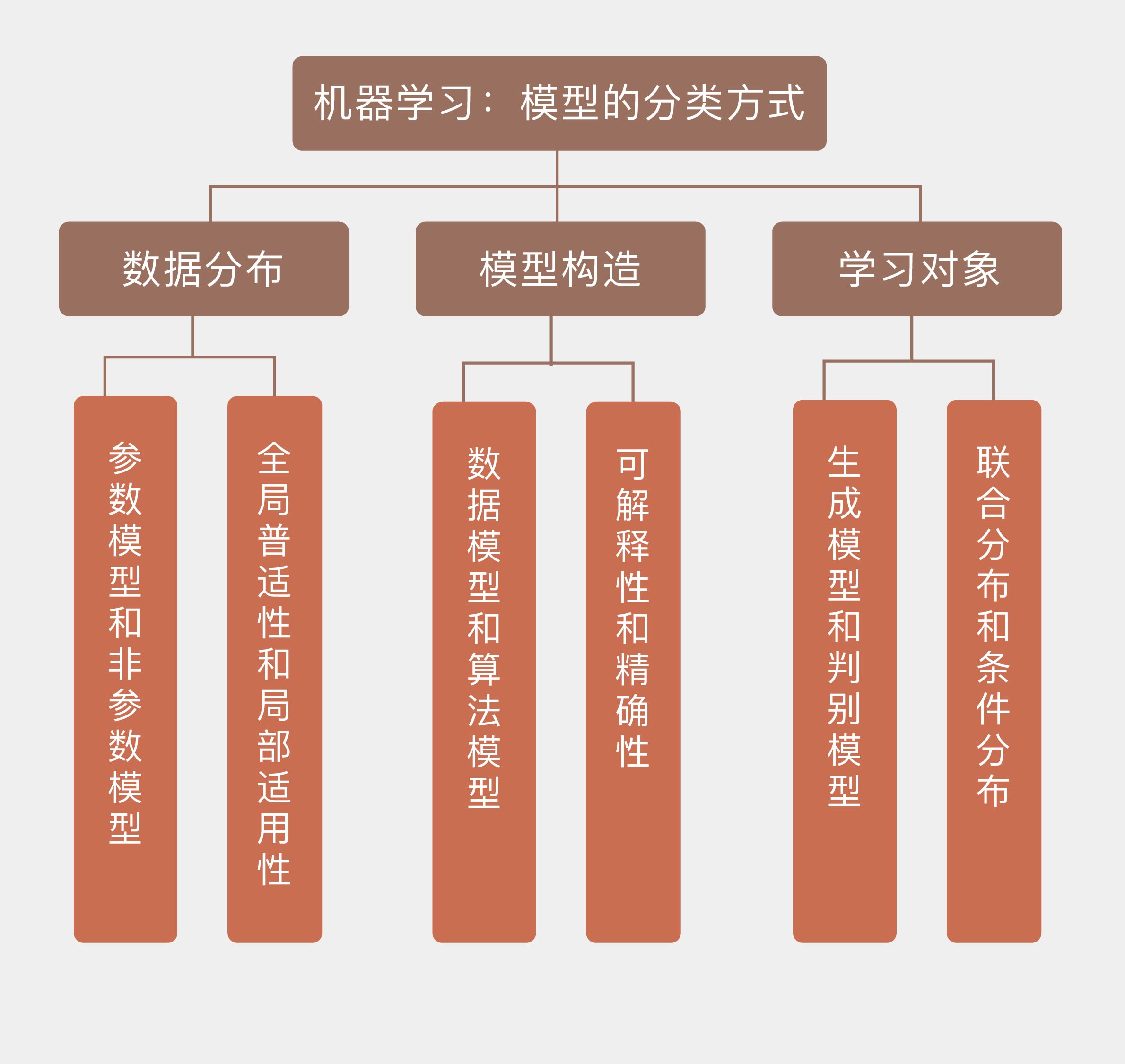
       从数据的角度看，如果待求解的概率分布或者数量关系可以用一组有限且固定数目的参数完全刻画，求出的模型就是参数模型（parametric model）；反过来，不满足这个条件的模型就是非参数模型（non-parametric model）。 

    参数模型的优点在于只用少量参数就完整地描述出数据的概率特性，参数集中的每个参数都具有明确的统计意义。 先验知识并不源于对数据的观察，而是先于数据存在，参数模型恰恰就是先验知识的体现与应用。  参数模型虽然简单实用，但其可用性却严重依赖于先验知识的可信度，也就是先验分布的准确程度。

   非参数模型意味着模型参数的数目是不固定的，并且极有可能是无穷大，这决定了非参数模型不可能像参数模型那样用固定且有限数目的参数来完全刻画。非参数模型其实可以理解为一种局部模型。

  从数据分布的角度看，不同的模型可以划分为参数模型和非参数模型两类。如果将这个划分标准套用到模型构造上的话，得到的结果就是数据模型（data model）和算法模型（algorithm model）。相比于参数对数据分布的刻画，这种分类方式更加侧重于模型对数据的拟合能力和预测能力。

   布雷曼将从输入 x 到输出 y 的关系看成黑盒，数据模型认为这个黑盒里装着一组未知的参数 θ，学习的对象是这组参数；算法模型则认为这个黑盒里装着一个未知的映射 f()˙，学习的对象也是这个映射。

如果说参数模型与非参数模型的核心区别在于数据分布特征的整体性与局部性，那么数据模型和算法模型之间的矛盾就是模型的可解释性与精确性的矛盾。

    还有另一种针对学习对象的划分方式，那就是生成模型和判别模型之分。简单地说，生成模型（generative model）学习的对象是输入 xx 和输出 yy 的联合分布 p(x,y)p(x,y)，判别模型学习的则是已知输入 xx 的条件下，输出 yy 的条件分布 p(y|x).两个分布可以通过贝叶斯定理建立联系。

    生成模型和判别模型的区别可以这样来理解：假如我被分配了一个任务，要判断一个陌生人说的是什么语言。如果用生成模型来解决的话，我就需要把这个老外可能说的所有语言都学会，再根据他的话来判定语言的种类。但可能等我学完这些语言时，这个陌生人都说不出话了。可是用判别模型就简单多了，我只需要掌握不同语言的区别就足够了。即使不会西班牙语或者德语的任何一个单词，单凭语感也可以区分出这两种语言，这就是判别模型的优势。