一道拉普拉斯逆变换练习题和对应的数值计算方法

Posted 2021-05-19 卓晴

摘 要： 针对于一些不太适合因式分解或者留数方法进行Laplace逆变换的问题，通过数值求解可以比较方便获得时域波形。本文给出了利用梯形积分方法进行Laplace逆变换，对于指数衰减周期方波进行逆变换。通过结果也指出了原来题目中使用exp(-3t)进行衰减所能够获得波形与题目给定的相差甚远。

关键词： 拉普拉斯变换，Laplace逆变换，数值计算，梯形积分

 

§01 练习题内容

---

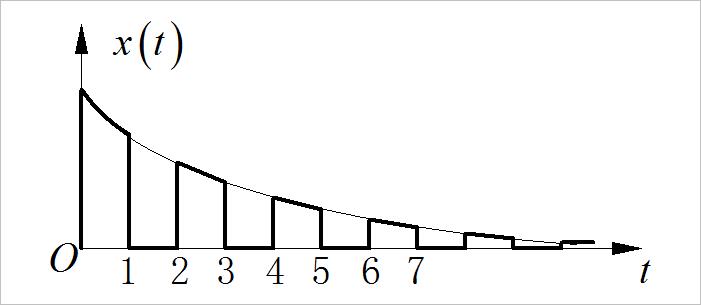
下面信号是有指数衰减信号 $e^{-3t}$和一个周期矩形信号 $x_p\left(t\right)$ 的相乘结果。求：信号 $x\left(t\right)$ 的拉氏变换。

$$x_p\left(t\right)=\sum _{n=0}^{+\infty }u\left(t-2n\right)-u\left(t-2n-1\right)$$

 

§02 经典求解方法

---

解：周期矩形脉冲信号的周期为2，第一个周期内的信号为：$$x_1\left(t\right)=u\left(t\right)-u\left(t-1\right)$$

它对应的拉普拉斯变换为：$$X_1\left(s\right)=\frac{1}{s}\left(1-e^{-s}\right)$$

周期矩形信号的拉普拉斯变换为：
$$X_p\left(s\right)=\frac{X_1\left(s\right)}{1-e^{-2s}}=\frac{1}{s}\left(1-e^{-s}\right)\frac{1}{1-e^{-2s}}=\frac{1}{s\left(1+e^{-s}\right)}$$

再根据s与平移性质：$$X_p\left(s\right)=\frac{1}{\left(s+3\right)\left(1+e^{-\left(s+3\right)}\right)}$$

 

§03 逆拉普拉斯变换

---

这个题目如果从时域波形求对应的拉普拉斯变换，根据上述过程就可以。但如果从$X\left(s\right)$反过来，求对应的时域信号，使用留数方法、因式分解法都不太容易。那么如何验证上述拉普拉斯变化是正确的呢？

1.逆Laplace数值计算

在 Laplace数值逆运算的讨论 讨论使用数值积分方法来求取信号Laplace逆变的方法。

对应的Laplace数值逆变换Python程序如下：

#------------------------------------------------------------
def invlt(t, fs, sigma, omiga, nint):
    omigadim = linspace(0, omiga, nint+1, endpoint=True)
    y = [(exp(1j*o*t) * fs(sigma+1j*o)).real for o in omigadim]
    y_left = y[:-1]
    y_right = y[0:]
    T = sum(y_right + y_left) * omiga/nint
    return exp(sigma*t) * T/ pi / 2

#------------------------------------------------------------
def fs(s):
    return 1/(s*s+1)

#------------------------------------------------------------
sigma = 0.2
omiga=200
nint=omiga*50

tdim = linspace(0, 2*pi* 3, 200)
ft = [invlt(t, fs, sigma, omiga, nint) for t in tdim]

在使用上述程序时，需要

• 对变量sigma设置正确取值，它应该是最右边的极点对应的实部大一点；
• 定义函数 fs(s)

2.本题参数

在本题中，极点包括：

• 实轴上 -3 处极点；
• 在虚轴上，每个2π有无穷多个极点；

所以 $sigma=0.1$。

3.数值计算结果

按照原题给出的参数，绘制出$e^{-3t}$衰减下波形。下面是对应的fs(s)函数定义。

def fs(s):
    return 1/((s+0.2)*(1+exp(-(s+0.2))))

变换出的结果如下。这与题目给定的示意图相差甚远。

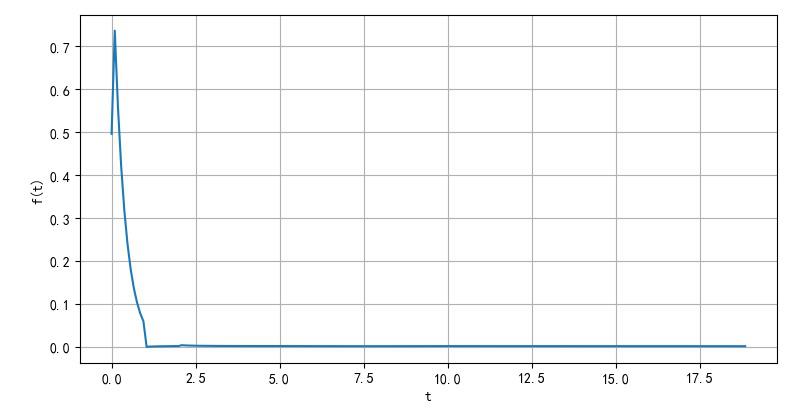
^{▲ exp(-3t)衰减的脉冲方波信号}

不过自己分析一下也马上会明白，实际上由于$e^{-3t}$衰减过快，所以最终只剩下第一个周期半个波形，随后的波形都衰减接近0.

将原来的函数参数修改一下，将指数衰减修改为：$e^{-0.1t}$。计算的波形如下图所示。这就与原题绘制的波形很接近了。

def fs(s):
    return 1/((s+0.1) * (1+exp(s+0.1)))

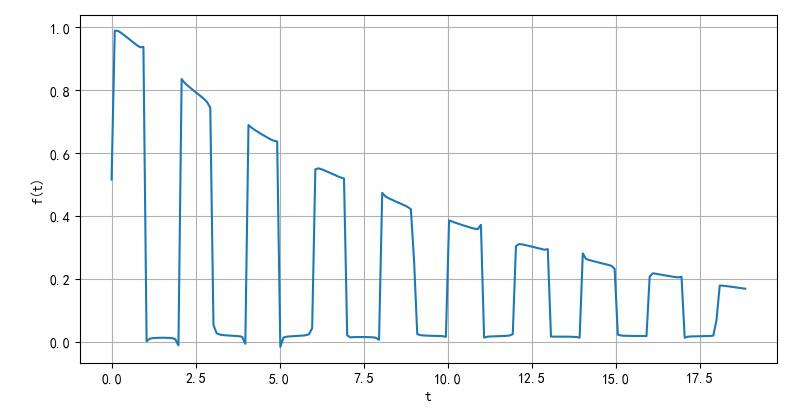
^{▲ exp(-0.1t)衰减的脉冲方波信号}

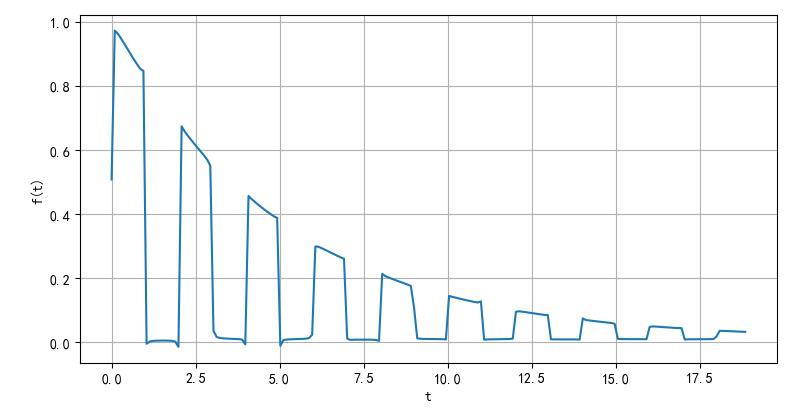
^{▲ exp(-0.2t)衰减的脉冲方波信号}

 

※ 结论讨论

---

针对于一些不太适合因式分解或者留数方法进行Laplace逆变换的问题，通过数值求解可以比较方便获得时域波形。本文给出了利用梯形积分方法进行Laplace逆变换，对于指数衰减周期方波进行逆变换。通过结果也指出了原来题目中使用exp(-3t)进行衰减所能够获得波形与题目给定的相差甚远。

 

---

■ 相关文献链接:

• Laplace数值逆运算的讨论