C++ 实现无向图的最小生成树Kruskal算法(完整代码)
Posted Wecccccccc
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了C++ 实现无向图的最小生成树Kruskal算法(完整代码)相关的知识,希望对你有一定的参考价值。
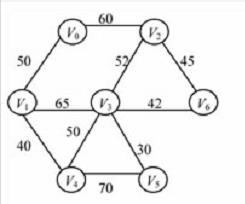
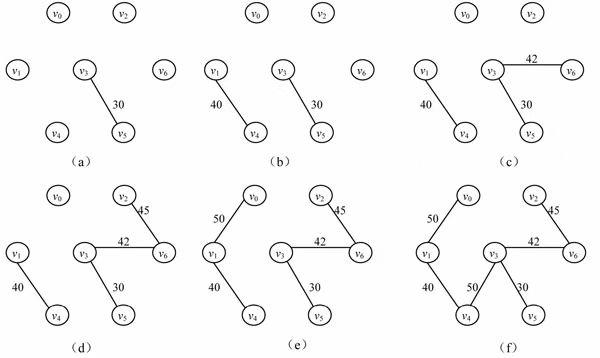
按照Kruskal思想,n个结点的生成树有n-1条边,故反复上述过程,直到选取了n-1条边为止,就构成了一棵最小生成树。
实现Kruskal算法的关键问题是:
当一条边加入T的边集中后,如何判断是否构成回路。
一种解决方法是定义一个一维数组f[n],存放T中每一个顶点所处连通分量的编号。
开始令f[i]=i,即图中每个顶点自成一个连通分量。
如果要往T的边集中增加一条边(vi, vj),首先检查f[i]和f[j]是否相同,若相同,则表明vi和vj处在同一连通分量中,加入此边必然形成回路;
若不相同,则不会形成回路,此时可以把此边加入生成树的边集中。
当加入一条新边后,必然将两个不同的连通分量连通,此时就需将两个连通分量合并,合并方法是将一个连通分量的编号换成另一个连通分量的编号。
下面以图的边表结构(用一个结构体存储图的顶点数、边数、顶点信息、边的信息)来存储一个带权的连通图,实现Kruskal算法如下:
#include <iostream>
#include <algorithm>
using namespace std;
const int MaxcertexNum = 30;
const int MaxEdge = 100;
typedef int VertexType;
class ENode
{
friend bool cmp(ENode a, ENode b);
friend class ELGraph;
private:
int vertex1;
int vertex2;
int weight;
};
class ELGraph
{
public:
ELGraph() {};
void CreateGraph();
void Kruskal(ENode TE[]);
private:
void Sort(ENode *a);
int vertexnum;
int edgenum;
VertexType vertexs[MaxcertexNum];
ENode edges[MaxcertexNum];
int f[MaxcertexNum];
int Find(int x)
{
if (f[x] != x) return Find(f[x]);
else return x;
};
void Union(int x, int y)
{
f[Find(y)] = Find(x);
}
};
bool cmp(ENode a, ENode b)
{
return a.weight < b.weight;
}
void ELGraph::Sort(ENode *a)
{
sort(a, a + edgenum, cmp);
}
void ELGraph::CreateGraph()
{
cout << "请输入顶点数和边数" << endl;
cin >> vertexnum >> edgenum;
cout << "请依次输入按序号0到n顶点的信息" << endl;
for (int i = 0; i < vertexnum; i++)
{
cin >> vertexs[i];
}
cout << "下面输入边表信息" << endl;
for (int i = 0; i < edgenum; i++)
{
int v1, v2, w;
cout << "输入边<i,j>对应的顶点序号i,j,再输入该边的权值" << endl;
cin >> v1 >> v2 >> w;
edges[i].vertex1 = v1;
edges[i].vertex2 = v2;
edges[i].weight = w;
}
}
void ELGraph::Kruskal(ENode TE[])
{
for (int i = 0; i < vertexnum; i++) f[i] = i;
Sort(edges);
int k = 0;
int j = 0;
while (k < vertexnum - 1)
{
int s1 = edges[j].vertex1;
int s2 = edges[j].vertex2;
if (Find(s1)!=Find(s2))
{
TE[k].vertex1 = s1;
TE[k].vertex2 = s2;
TE[k].weight = edges[k].weight;
k++;
Union(s1, s2);
}
j++;
}
for (int i = 0; i < vertexnum - 1; i++)
{
cout << TE[i].vertex1 << "->" << TE[i].vertex2 << " " << TE[i].weight << endl;
}
}
int main()
{
ELGraph g;
g.CreateGraph();
ENode TE[50];
g.Kruskal(TE);
return 0;
}
测试结果:
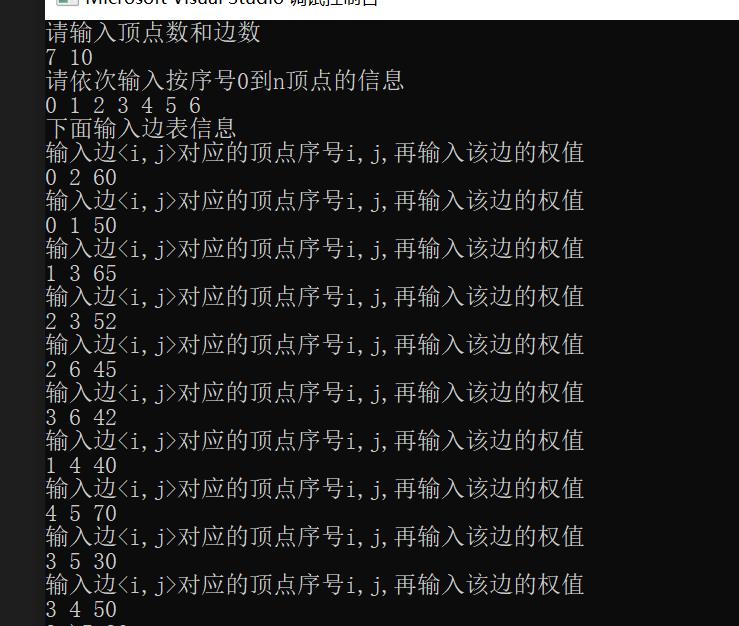

以上是关于C++ 实现无向图的最小生成树Kruskal算法(完整代码)的主要内容,如果未能解决你的问题,请参考以下文章
无向带权图的最小生成树算法——Prim及Kruskal算法思路