对于任给的一张无向带权连通图,求出其最小生成树(C++)
Posted 唐火
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了对于任给的一张无向带权连通图,求出其最小生成树(C++)相关的知识,希望对你有一定的参考价值。
对于任给的一张无向带权连通图,求出其最小生成树。
题目要求:
(1)编程创建一幅图
(2)输出创建的图
(3)编写Prim算法代码,实现图的最小生成树求解,且输出最小生成树
(4)编写Kruskal算法代码,实现图的最小生成树求解,且输出最小生成树
(5)编写菜单,允许用户选择相应操作
代码如下:
#include <iostream>
#include <queue>
#include <algorithm>
using namespace std;
const int maxVertexNum = 30;//最大顶点数
const int noEdge = 99999999;//用来记录两个顶点之间没有边
const int ERROR = -1;//发生错误
class Graph
private :
class Edge
public :
int v1;
int v2;
int w;
;
int edgeNum;//边数
int vertexNum;//顶点数
int vertexs[maxVertexNum][maxVertexNum];//邻接矩阵
bool vis[maxVertexNum];//用来标记是否访问过该顶点
int dist[maxVertexNum];//prim算法中用来记录该结点离最小生成树的距离
int parent[maxVertexNum];//prim算法中用到
Edge edge[maxVertexNum];//用来记录边,方便输出
int totalWeight;//最小权重和
int set[maxVertexNum];//kruskal算法中,集合数组,利用并查集算法,来判断是否构成回路
Edge kEdge[maxVertexNum];//kruskal算法中所用,用来记录创建的图的信息,在用kruskal算法时,不是用邻接矩阵存储的图,而是用了这个结构体数组来存储
public:
void menu()
char c;
while (true)
cout << "--------邻接矩阵存储的图--------------" << endl;
cout << "--------输入 c 创建图-----------------" << endl;
cout << "--------输入 p 输出图-----------------" << endl;
cout << "--------输入 r 使用prim算法-----------" << endl;
cout << "--------输入 k 使用kruskal算法--------" << endl;
cout << "--------输入 e 退出程序---------------" << endl;
cout << "---------顶点从0开始------------------" << endl;
cin >> c;
switch (c)
case 'c':
buildGraph();
cout << "创建完毕,按任意键继续" << endl;
c = getchar();//吃回车
c = getchar();//吃任意键
system("cls");//刷新屏幕
break;
case 'p':
printGraph();
cout << "输出完毕,按任意键继续" << endl;
c = getchar();
c = getchar();
system("cls");
break;
case 'r':
prim();
cout << "输出完毕,按任意键继续" << endl;
c = getchar();
c = getchar();
system("cls");
break;
case 'k':
kruskal();
cout << "输出完毕,按任意键继续" << endl;
c = getchar();
c = getchar();
system("cls");
break;
case 'e':
return;
Graph() :vertexNum(0), edgeNum(0)
initVis();
for (int i = 0; i < maxVertexNum; i++)
for (int j = 0; j < maxVertexNum; j++)
vertexs[i][j] = noEdge;
private:
void initSet()
for (int i = 0; i < vertexNum; i++) set[i] = i;
void Union(int root1, int root2)
int x = Find(root1);
int y = Find(root2);
if (x != y)
set[x] = y;
int Find(int x)
if (set[x] != x) return Find(set[x]);
else return x;
void initVis()
for (int i = 0; i < maxVertexNum; i++)
vis[i] = false;
void buildGraph()
cout << "请输入节点数和边数" << endl;
cin >> vertexNum >> edgeNum;
int e1, e2;
int w;
for (int i = 0; i < edgeNum; i++)
cin >> e1 >> e2>>w;
vertexs[e1][e2] = w;
vertexs[e2][e1] = w;
kEdge[i].v1 = e1;
kEdge[i].v2 = e2;
kEdge[i].w = w;
void printGraph()
for (int i = 0; i < vertexNum; i++)
vis[i] = true;
for (int j = 0; j < vertexNum; j++)
if (!vis[j]&&vertexs[i][j] != noEdge)
cout << i << " - " << j <<" = "<<vertexs[i][j]<< endl;
initVis();
int findMinDist()
int minVertex;
int minDist = noEdge;
for (int i = 0; i < vertexNum; i++)
if (dist[i] != 0 && dist[i] < minDist)
minDist = dist[i];
minVertex = i;
if (minDist < noEdge) return minVertex;
else return ERROR;
void prim()
for (int i = 0; i < vertexNum; i++)
dist[i] = vertexs[0][i];
parent[i] = 0;
totalWeight = 0;
int cnt = 0;
dist[0] = 0;
parent[0] = -1;
cnt++;
int v;
while (true)
v = findMinDist();
if (v == ERROR) break;
edge[cnt].v1 = parent[v];
edge[cnt].v2 = v;
edge[cnt].w = dist[v];
totalWeight += dist[v];
dist[v] = 0;
cnt++;
for (int w = 0; w < vertexNum; w++)
if (dist[w] != 0 && vertexs[v][w] < noEdge)
dist[w] = vertexs[v][w];
parent[w] = v;
if (cnt < vertexNum)
cout << "此图不连通" << endl;
else
for (int i = 1; i < cnt; i++)
cout << edge[i].v1 << " - " << edge[i].v2 << " = " << edge[i].w << endl;
cout <<"totalWeight = " <<totalWeight << endl;
//所有普通类成员函数,都不能以函数指针的方式作为其他函数的入口函数。
//所以这里的cmp函数要加上static
static bool cmp(Edge a, Edge b)
return a.w < b.w;
void kruskal()
initSet();
sort(kEdge,kEdge+edgeNum,cmp);
int cnt = 0;
int idx = 0;
totalWeight = 0;
while (cnt < vertexNum - 1 && idx < edgeNum)
int v1 = kEdge[idx].v1;
int v2 = kEdge[idx].v2;
if (Find(v1) != Find(v2))
edge[cnt].v1 = v1;
edge[cnt].v2 = v2;
edge[cnt].w = kEdge[cnt].w;
totalWeight += edge[cnt].w;
cnt++;
Union(v1, v2);
idx++;
if (cnt < vertexNum - 1)
cout << "此图不连通" << endl;
else
for (int i = 0; i < vertexNum - 1; i++)
cout << edge[i].v1 << " - " << edge[i].v2 << " = " << edge[i].w << endl;
cout << "totalWeight = " << totalWeight << endl;
;
int main()
Graph g;
g.menu();
return 0;
示例:
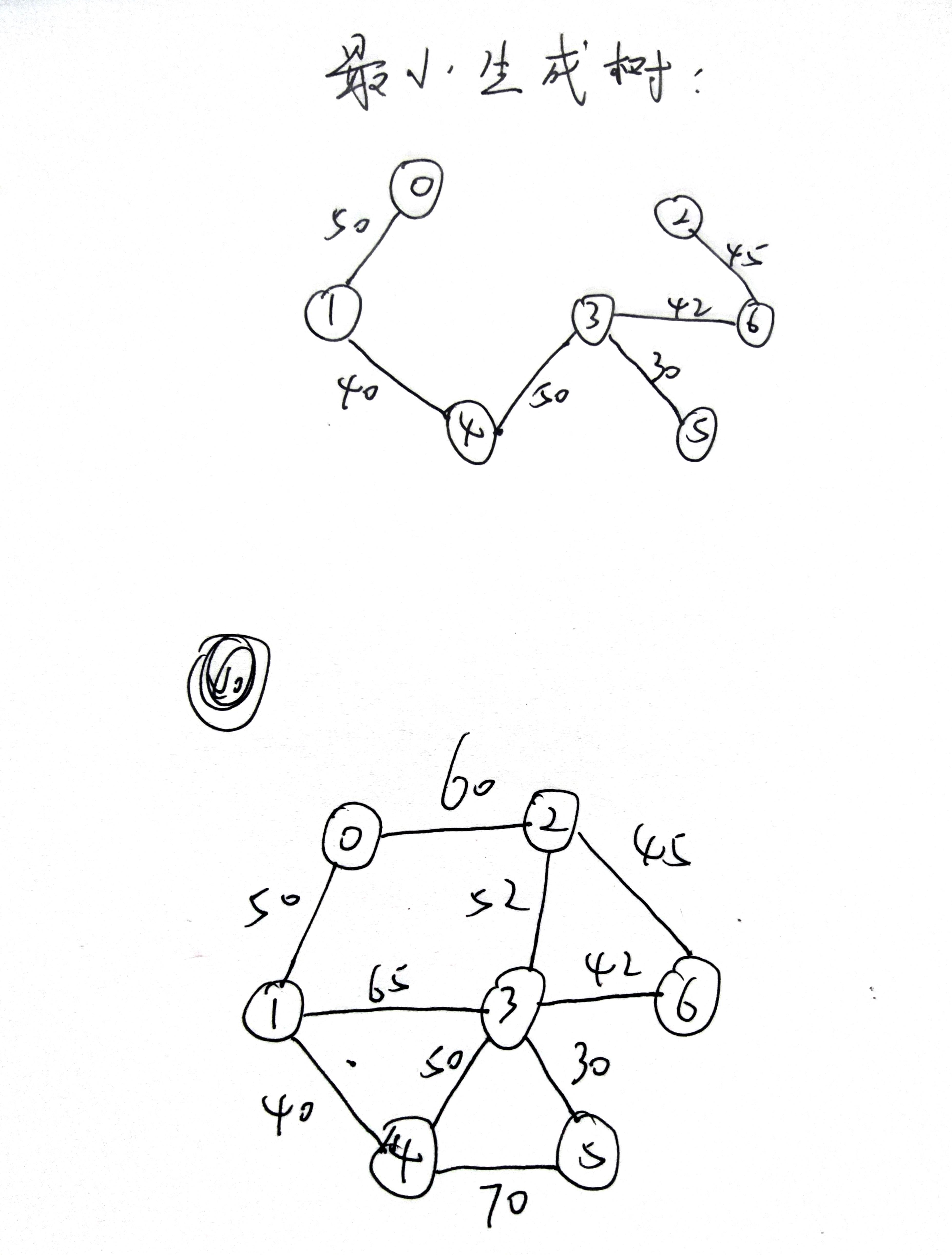
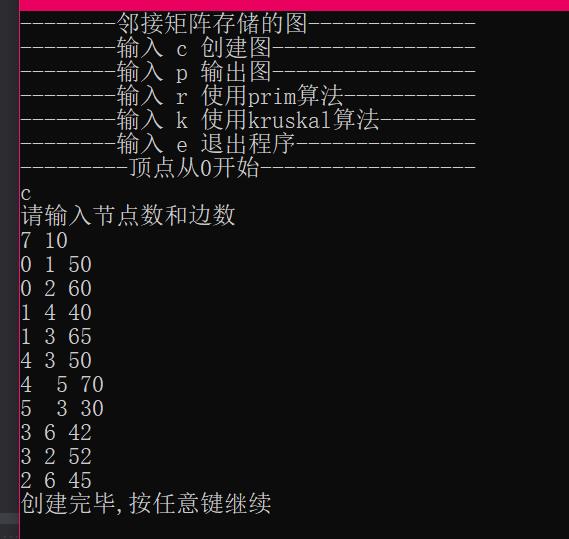
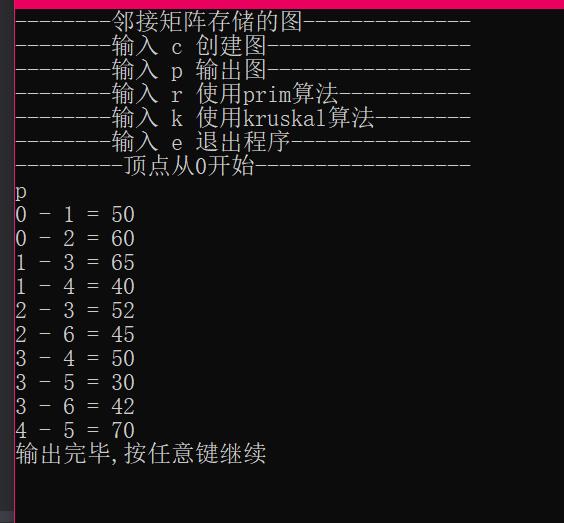
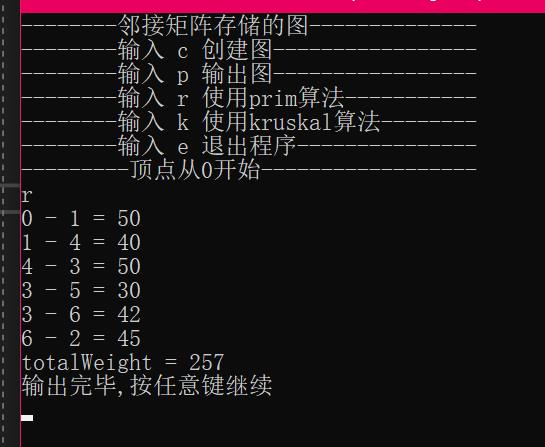
以上是关于对于任给的一张无向带权连通图,求出其最小生成树(C++)的主要内容,如果未能解决你的问题,请参考以下文章