求大佬用java帮我实现dijkstra算法，单源最短路径

Posted 2023-03-21

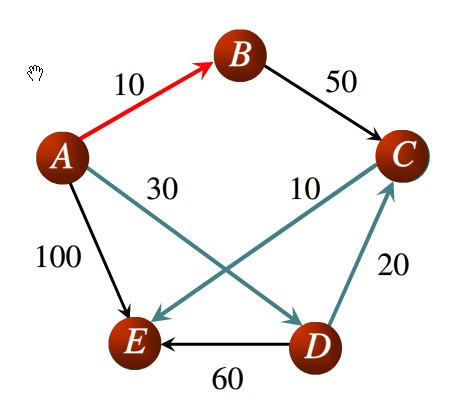
求大佬用java帮忙写一下这个图的单源最短路径算法，dijkstra的，谢谢了！！！

参考技术A

import heapq
from collections import defaultdict
edges = [["A","B"],["A","D"],["A","E"],["B","C"],["C","E"],["D","E"],["D","C"]]
dist = [10,30,100,50,10,60,20]
res = []
def dijkstra(e,dist,start,end):
‍   hm = defaultdict(list)
‍   for i in range(len(e)):
‍   ‍   hm[e[i][0]].append((e[i][1],dist[i]))
‍   r =
‍   r[start] = 0
‍   q = [(0,start,[start])]
‍   while q:
‍   ‍   dis,node,res = heapq.heappop(q)
‍   ‍   if node == end:
‍   ‍   ‍   return dis,res
‍   ‍   for u,v in hm[node]:
‍   ‍   ‍   t = dis+v
‍   ‍   ‍   if u not in r or t < r[u]:
‍   ‍   ‍   ‍   r[u] = t
‍   ‍   ‍   ‍   heapq.heappush(q,(t,u,res+[u]))
‍   return 0,[]
dijkstra(edges,dist,"A","E")

参考技术B public void test()
//初始化矩阵，记录路径数据
int SIZE = 5;
int[][] data = new int[SIZE][SIZE];
for (int i = 0; i < SIZE; i ++)
for (int j = 0; j < SIZE; j ++)
data[i][j] = -1;


data[0][1] = 10;
data[0][3] = 30;
data[0][4] = 100;
data[1][2] = 50;
data[2][4] = 10;
data[3][4] = 60;
data[3][2] = 20;

//计算最小距离结果
Map<String, List<Integer>> minPaths = calcPath(data);

//在结果内反向从终点检索最近距离路径
List<Integer> minPath = new ArrayList<>();
int lastPathPoint = SIZE - 1;
while (true)
minPath.add(lastPathPoint);
lastPathPoint = minPaths.get("lastPathPoints").get(lastPathPoint);
if (lastPathPoint == -1)
break;



//输出最近路径
for (int i = minPath.size() - 1; i >= 0; i --)
System.out.printf("\033[31m%c \033[0m", minPath.get(i) + 'A');
if (i != 0)
System.out.print("-> ");





/**
* 计算最短路径统计
* 从起点开始挨个计算距离当前已计算点集合最近的点并记录加入集合
* @param data
* @return
*/
private Map<String, List<Integer>> calcPath(int[][] data)
Map<String, List<Integer>> result = new HashMap<>();
List<Integer> points = new ArrayList<>();
List<Integer> distances = new ArrayList<>();
List<Integer> lastPathPoints = new ArrayList<>();

//初始化：所有点的距离为-1，所有点最近路径的上一个点为-1
for (int i = 0; i < data.length; i ++)
distances.add(-1);
lastPathPoints.add(-1);


//挨个检查当前集合所有点的相邻点，找出最近距离点
points.add(0);
distances.set(0, data[0][0]);
Set<Integer> completePoints = new HashSet<>(); //已无需要检查相邻点的点，减少后续检查
while (points.size() < data.length)
int minPoint = -1;
int minDistance = -1;
int minPathPoint = -1;
for (Integer point : points)
if (completePoints.contains(point)) //该点已被记录无需再检查，跳过
continue;

//检查当前点相邻点
boolean hasConnectPoint = false;
for (int i = 0; i < data[point].length; i ++)
if (data[point][i] == -1) //不是相邻点
continue;

if (distances.get(i) >= 0) //该相邻点已在集合内
continue;

hasConnectPoint = true;
if (data[point][i] + distances.get(point) < minDistance || minDistance == -1) //新的最近点
minPoint = i;
minDistance = data[point][i] + distances.get(point);
minPathPoint = point;


if (!hasConnectPoint) //无需要检查的相邻点，记录以减少下次检查
completePoints.add(point);


if (minPoint == -1) //已无点与当前集合相连
break;

points.add(minPoint);
distances.set(minPoint, minDistance);
lastPathPoints.set(minPoint, minPathPoint);


result.put("points", points);
result.put("distances", distances);
result.put("lastPathPoints", lastPathPoints);
return result;

用小根堆实现dijkstra，求图的单源最短路径

小根堆实现dijkstra

求图的最短路径，最常用的有四种方法：

1.Floyed（弗洛伊德）算法。最简单的最短路径算法，可以求多源最短路径。时间复杂度为O(n*n*n)。

2.Dijkstra（迪杰斯特拉）算法。只能求单源最短路径。时间复杂度为O(n*n)。

3.Bellman-Ford（贝尔曼福德）算法。只能求单源最短路径。时间复杂度为O(NE)（N为顶点数，E是边数）。

4.SPFA算法。为Bellman-Ford算法的队列实现，减少不必要的冗杂计算。只能求单源最短路径。时间复杂度为O(kE)（k是常数，平均值为2）。

由以上算法可知求单源最短路径，SPFA一般情况为耗时最少的。

但我们也使用Dijkstra算法。但它的时间复杂度也太高，于是我们就用小根堆优化Dijkstra，减少冗杂操作，达到减少时间的目的。

最好使用STL的优先队列来模拟小根堆，由于STL中的优先队列自动设为大根堆，所以我们把队列里的每个量都乘以-1，达到目的。

以下为代码实现:

 1 #include<cstdio>
 2 #include<queue>
 3 #define N 420000
 4 using namespace std;
 5 priority_queue<int>s;//优先队列 
 6 int num_edge,head[N],a,b,c,d[N],n,m,x,y,p[N];
 7 struct hehe{
 8     int next;
 9     int to;
10     int dis;
11 }edge[N];
12 void add_edge(int from,int to,int dis){
13     edge[++num_edge].next=head[from];
14     edge[num_edge].to=to;
15     edge[num_edge].dis=dis;
16     head[from]=num_edge;
17 }
18 void dijkstra(){
19     s.push(-a);//由于优先队列自动设为大根堆，所以可以把其中所有量都乘以-1，达到使用小根堆的要求 
20     for(int i=1;i<=n;++i)
21         d[i]=4200000;
22     d[a]=0;
23     while(!s.empty()){
24         x=s.top();//取出队首元素 
25         p[-x]=1;
26         s.pop();//删除队首元素 
27         for(int i=head[-x];i;i=edge[i].next){
28             y=edge[i].to;
29             if(p[y]==1)
30                 continue;
31             if (d[y]>d[-x]+edge[i].dis){
32                 d[y]=d[-x]+edge[i].dis;
33                 if(!p[y])
34                     s.push(-y);//加入一个遍历元素 
35             }
36         }
37     }
38 }
39 int main(){
40     scanf("%d%d",&n,&m);
41     for(int i=1;i<=m;++i){
42         scanf("%d%d%d",&a,&b,&c);
43         add_edge(a,b,c);
44         add_edge(b,a,c);
45     }
46     scanf("%d%d",&a,&b);//求a到b的最短路径 
47     dijkstra();
48     printf("%d",d[b]);
49     return 0;
50 }

View Code