时间序列预测ARIMA模型实践（SPSS应用）

Posted 2021-05-02 胡大大数据

• 时间序列分析基本原理与基础方法请参考《地理数学方法》课程时间序列分析章节
  

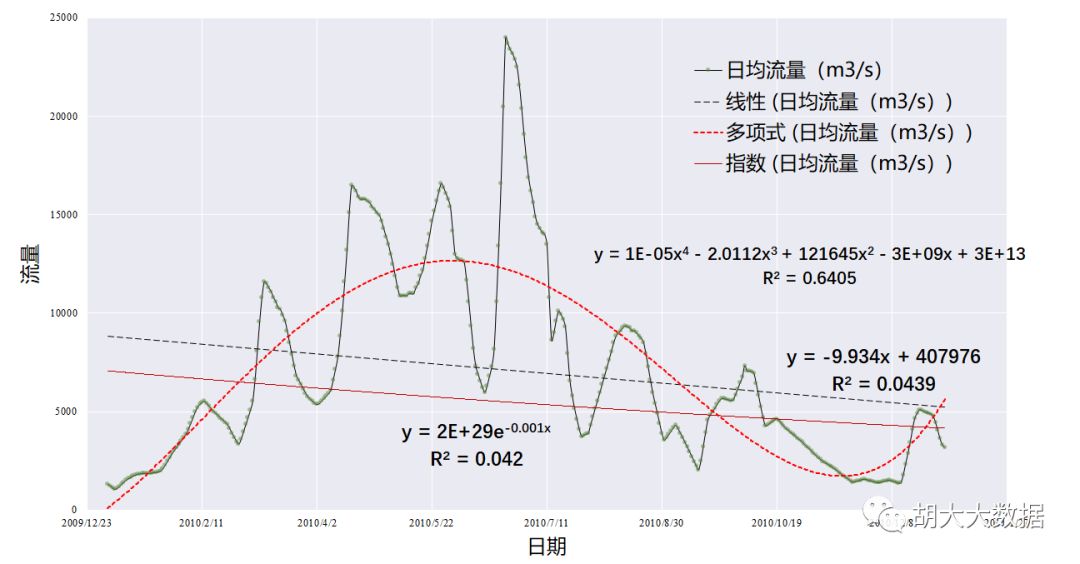
• 平稳性严格定义：时间序列随机变量的所有统计特征都是独立于时间分布

• 平稳性简要判别：时间序列无趋势无周期性，均值延时间轴常量震荡，方差随时间变化趋于稳定

• 强平稳：均值函数是常数函数且协方差函数仅与时间差相关

• 检验方法：ADF、KPSS、PP……

• 差分处理：去除趋势使时间序列平稳

•差分自回归移动平均模型，其基本模型可表示为

ARIMA(p,d,q)

•其中p是自回归模型阶数，d是差分阶数，q是移动(滑动)平均项数。

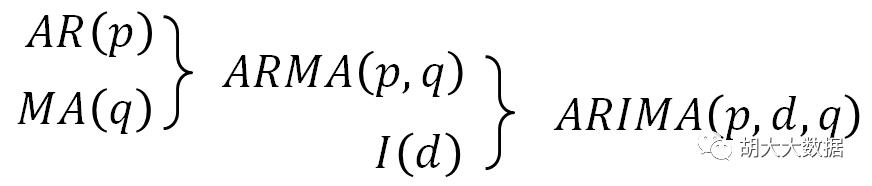
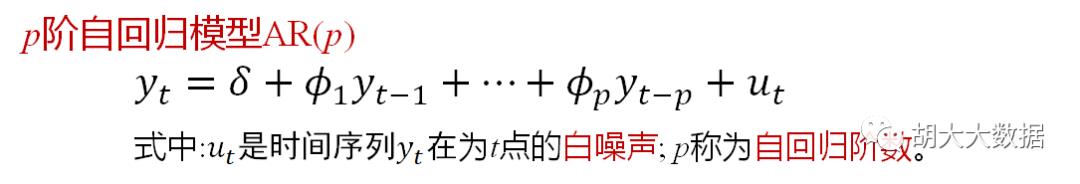
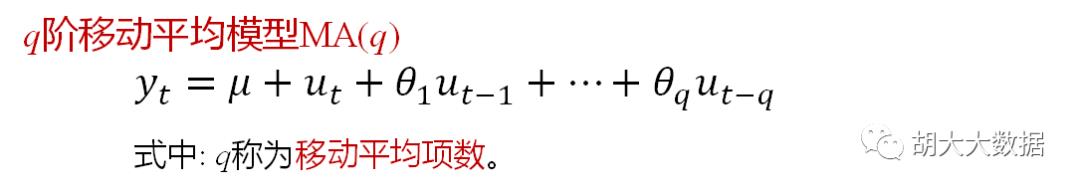
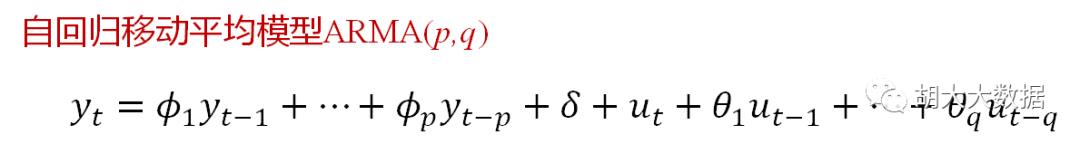
差分自回归移动平均模型ARIMA(p,d,q)

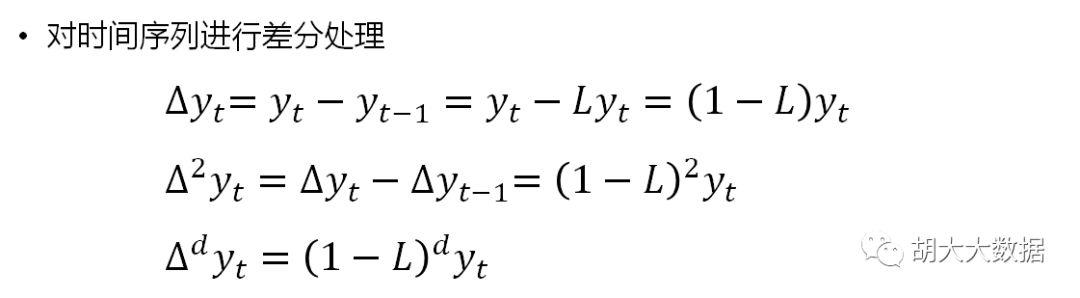
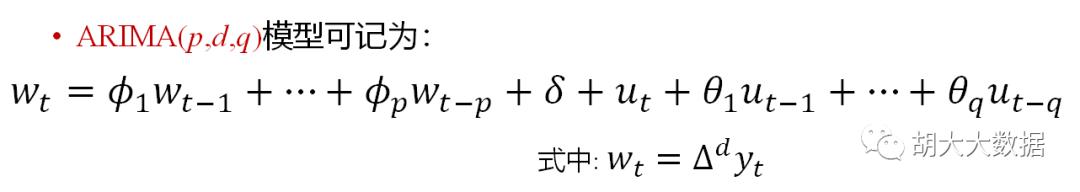
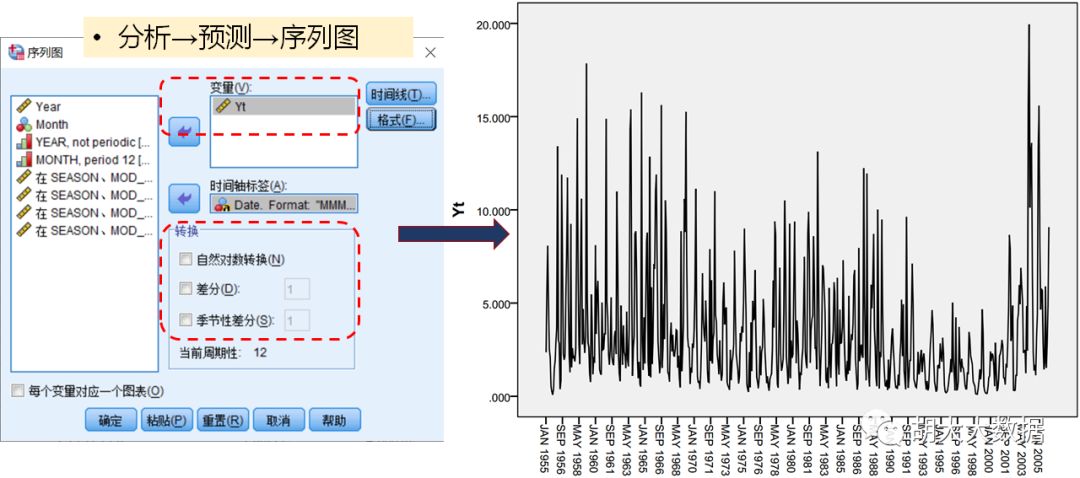
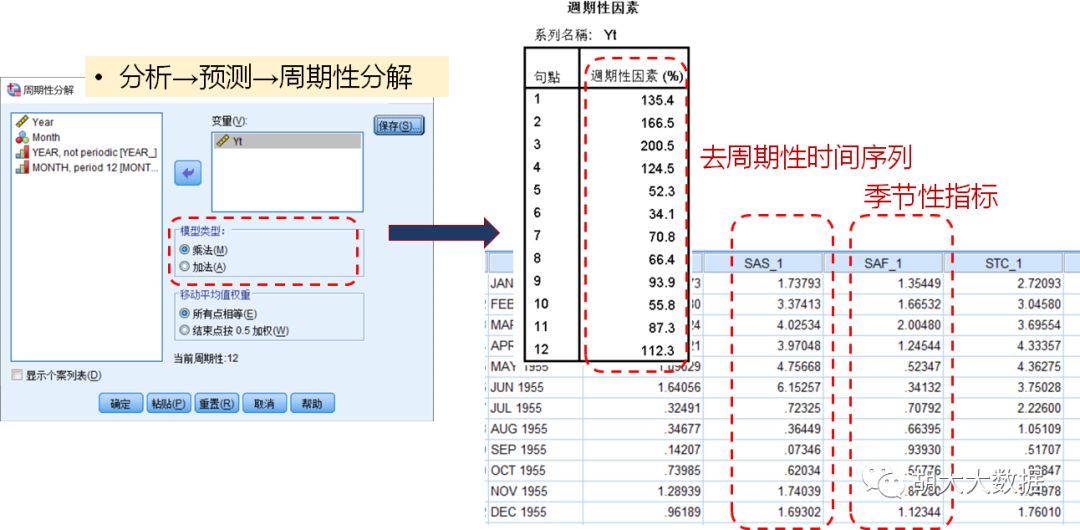
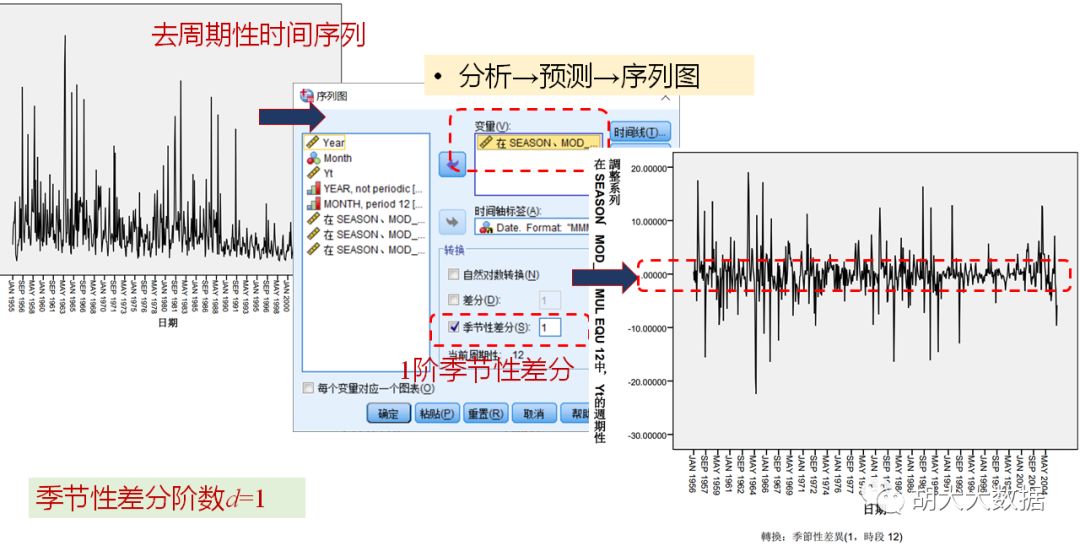
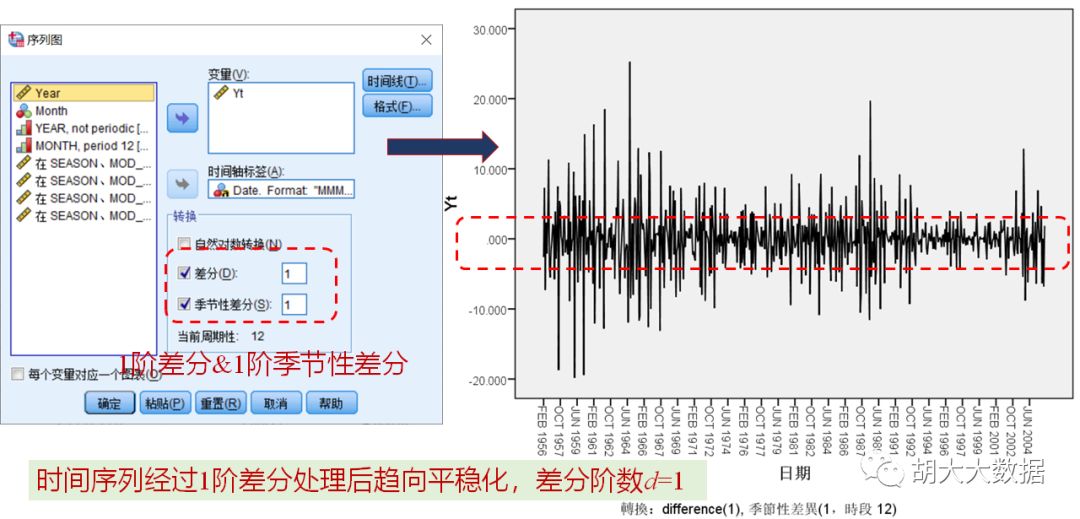
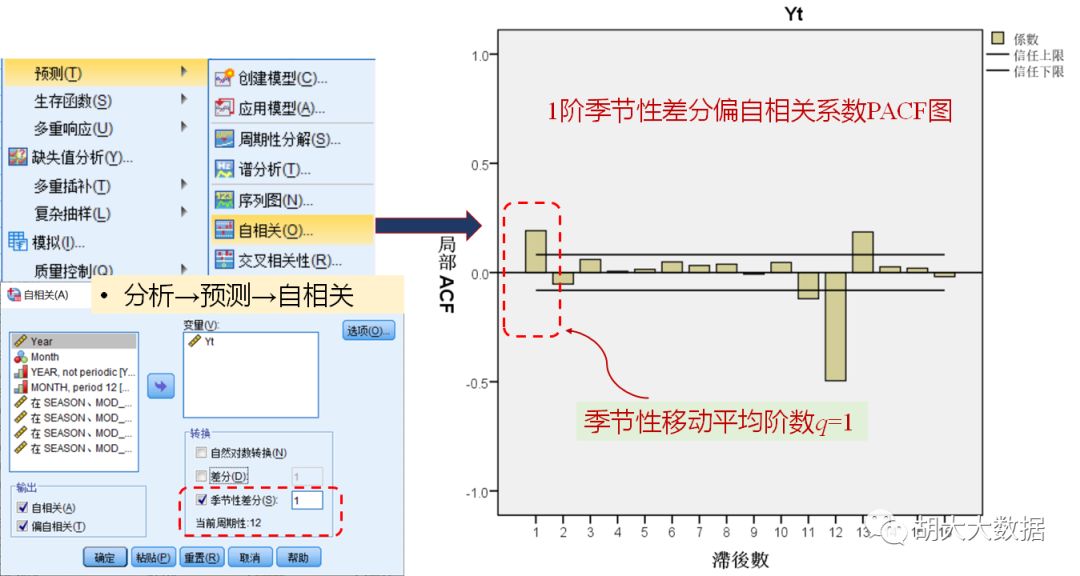
• Step-1: 时间序列数据可视化，观察其季节性与平稳性特征。非平稳时间序列进行(季节性)差分处理，得到去周期性平稳序列及(季节性)差分阶数d。

• Step-2: 选取合适模型，确定ARIMA模型的自回归阶数p与移动平均项数q。

• 平稳化处理后，若自相关函数ACF是拖尾的，偏自相关函数PACF是截尾的，建立AR模型；

• 若自相关函数ACF是截尾的，偏自相关函数PACF是拖尾的，建立MA模型；

• 若自相关函数ACF与偏自相关函数PACF均是拖尾的，建立ARMA模型。

• Step-4: AR/MA/ARIMA模型参数估计。

• Step-5: 假设检验，诊断残差序列是否为白噪声序列，应用模型进行预测。

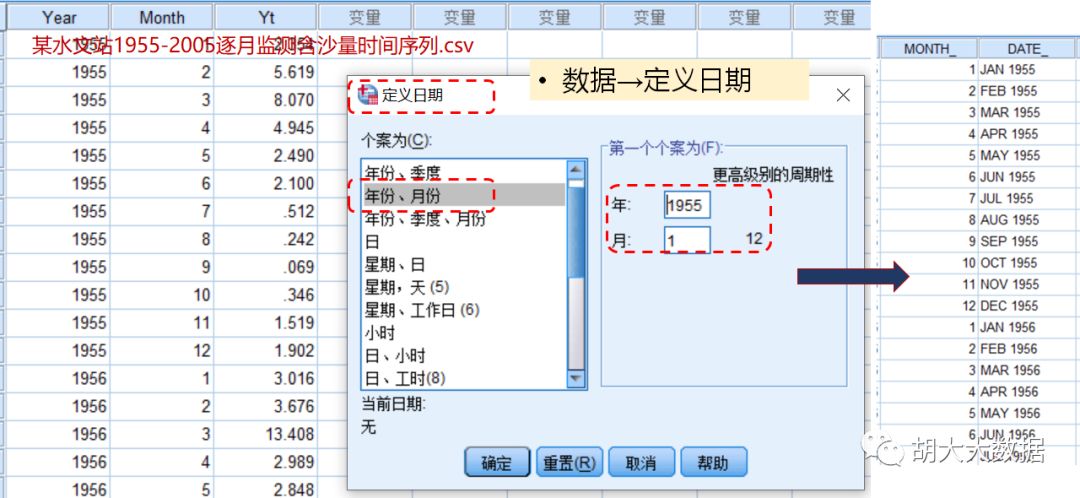
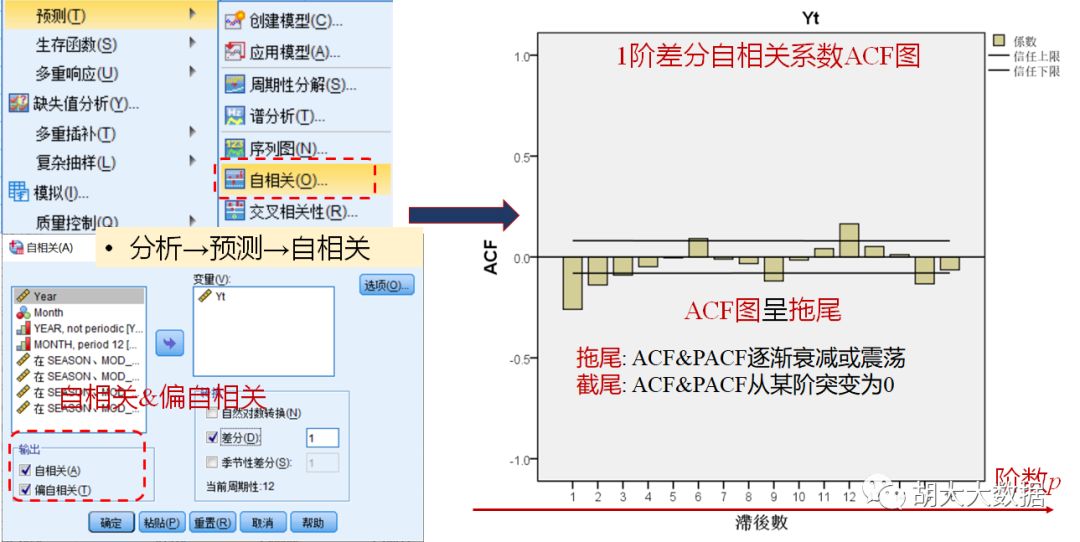
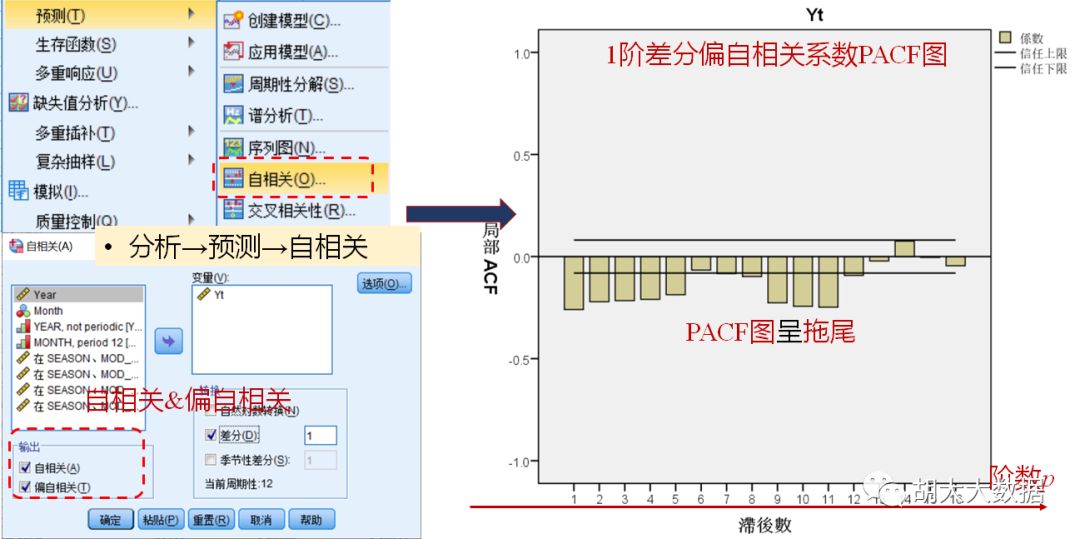
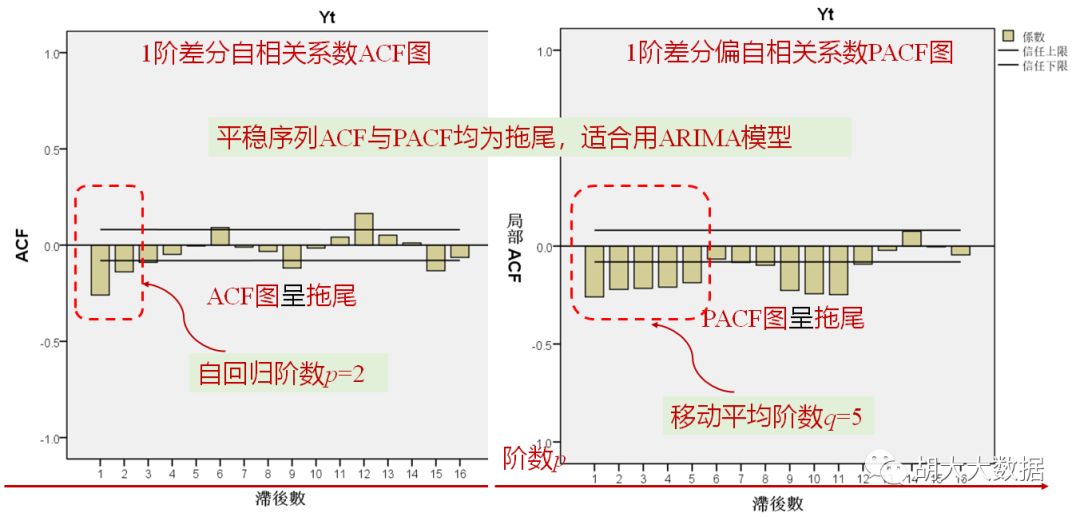
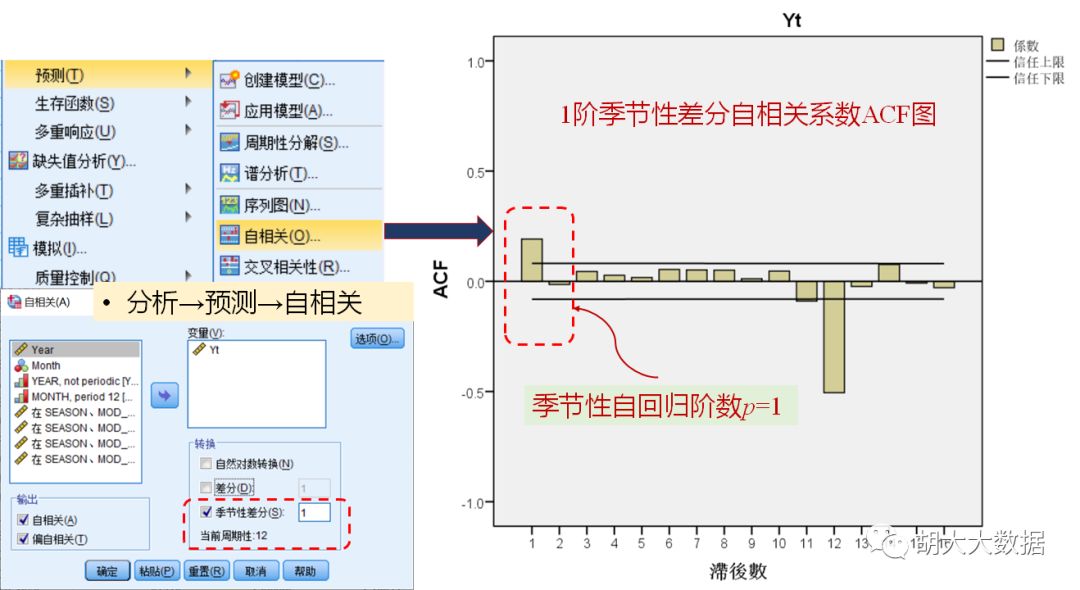
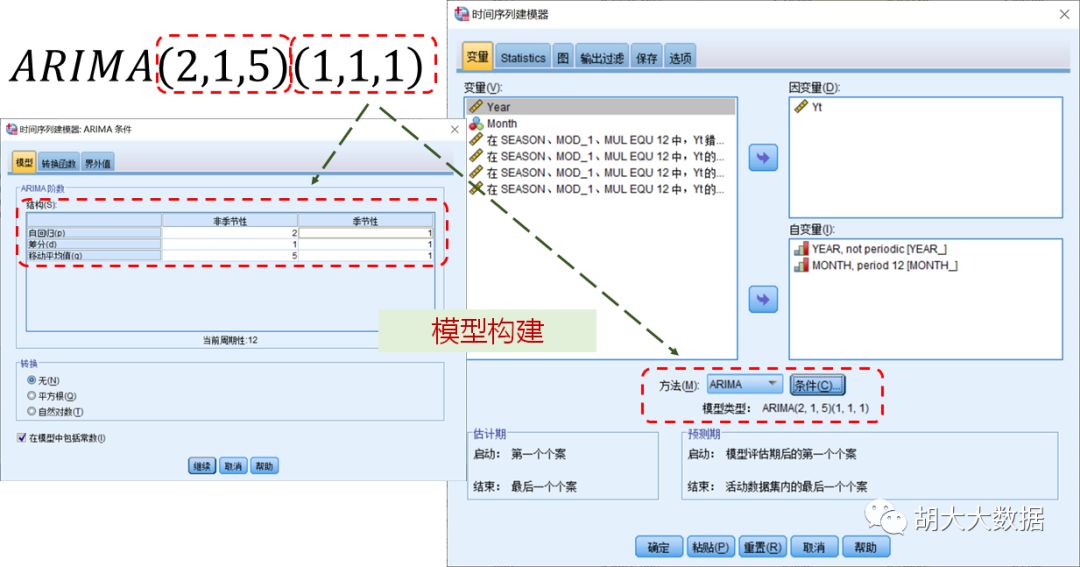
确定模型参数，最终选定为ARIMA(2,1,5)(1,1,1)

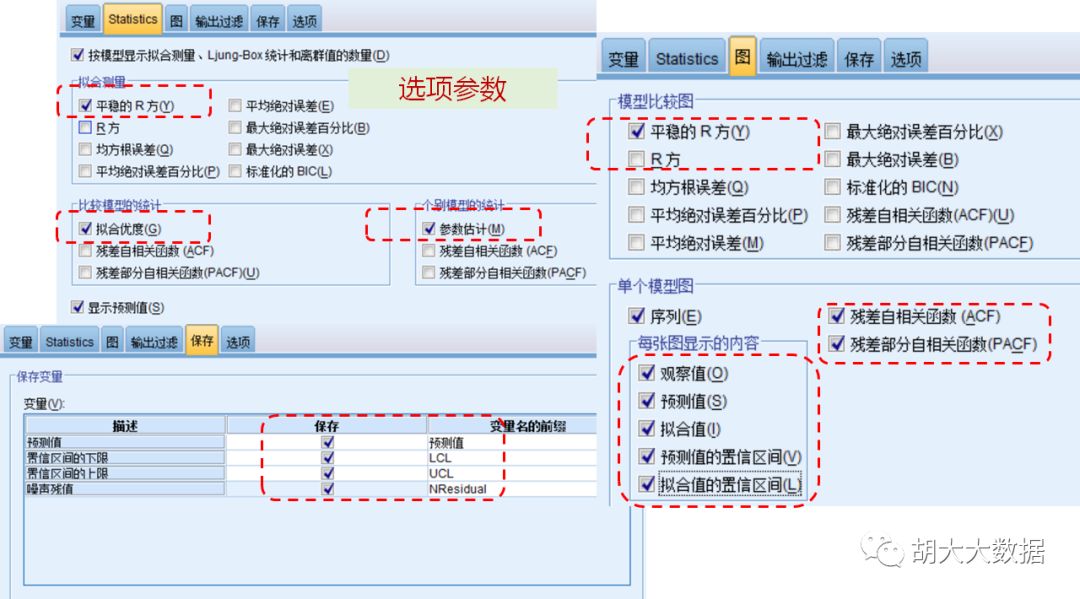
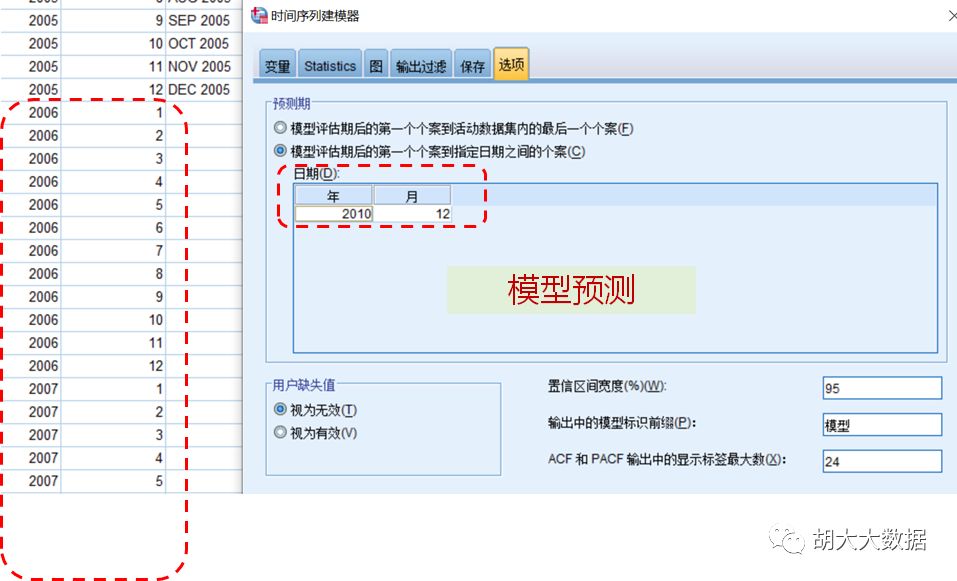
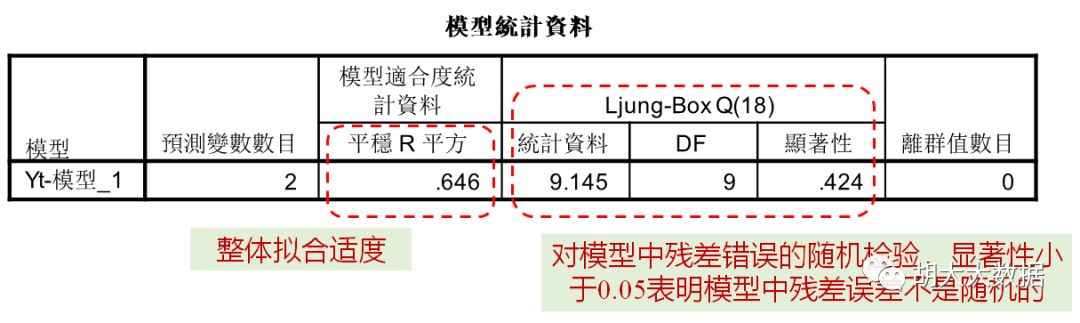
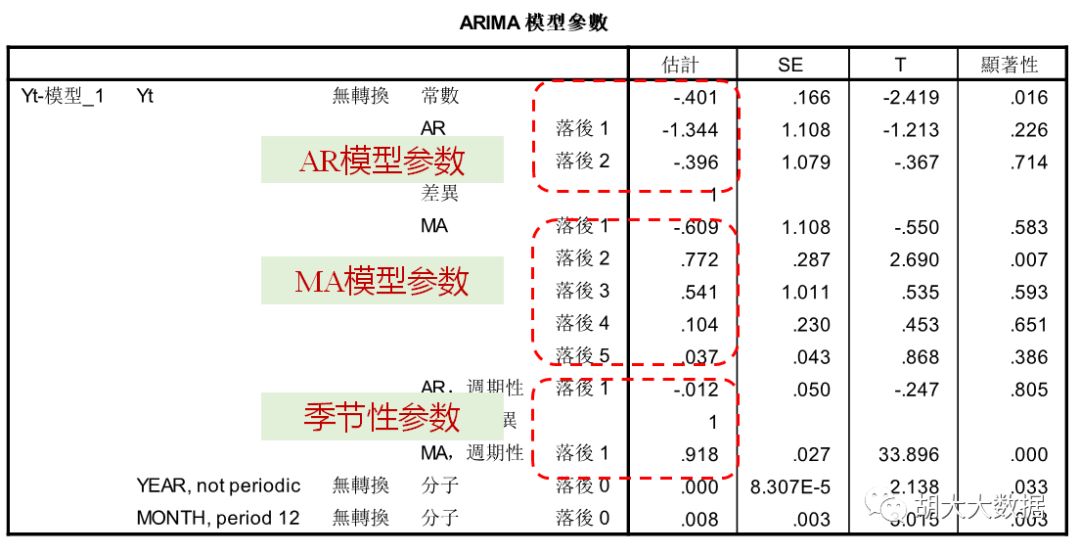
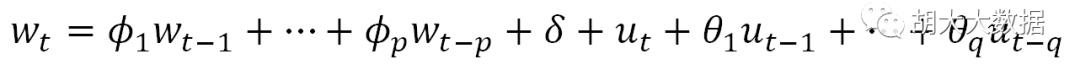
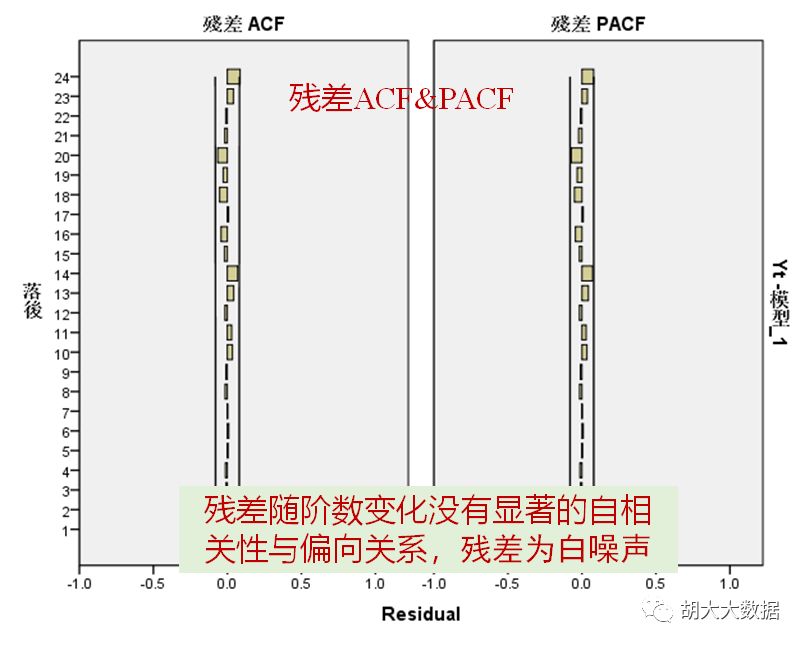
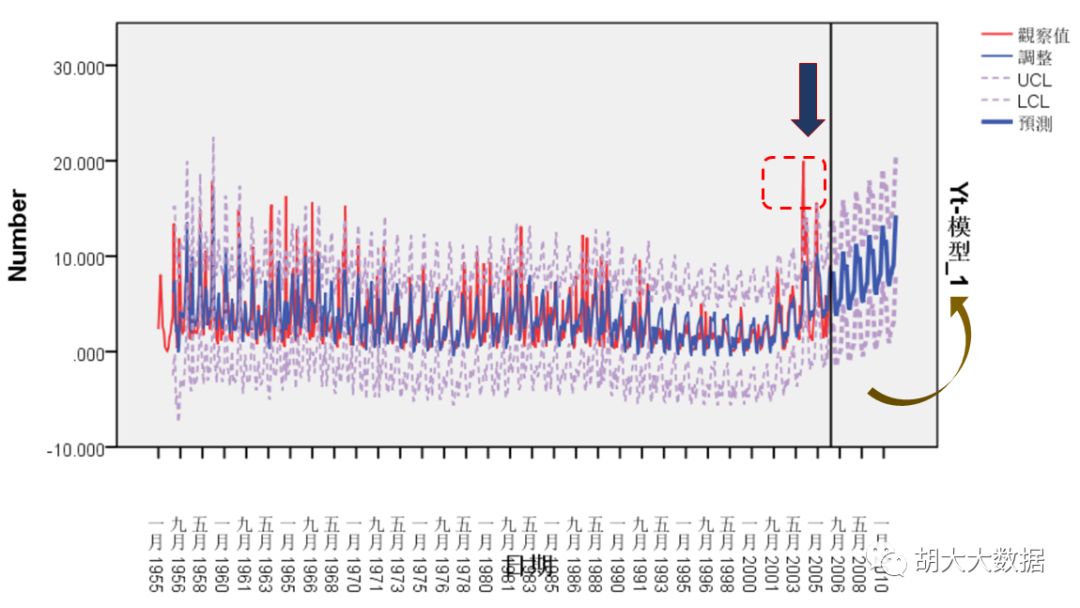
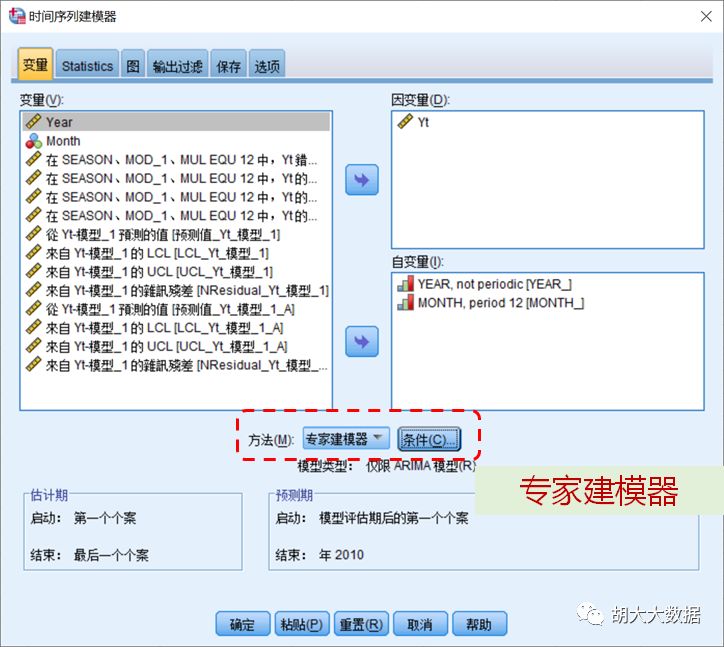
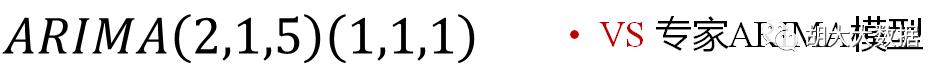
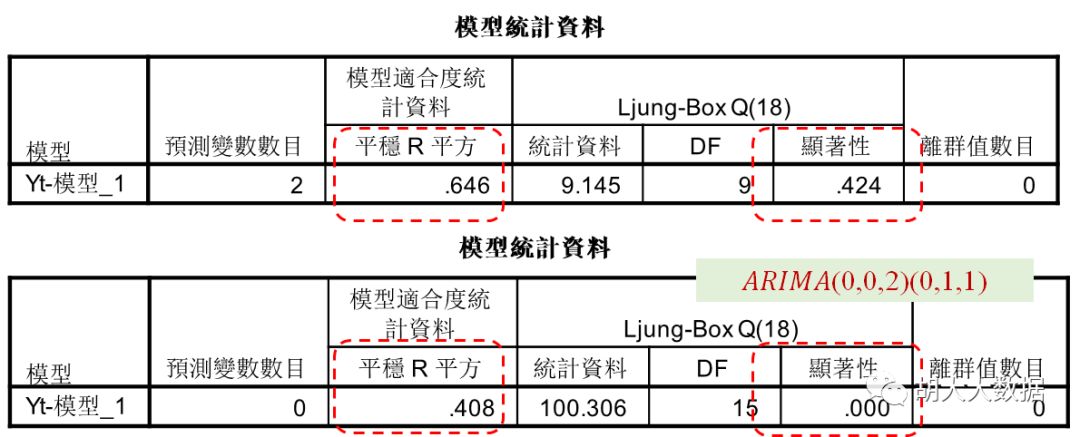
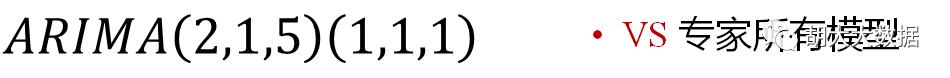
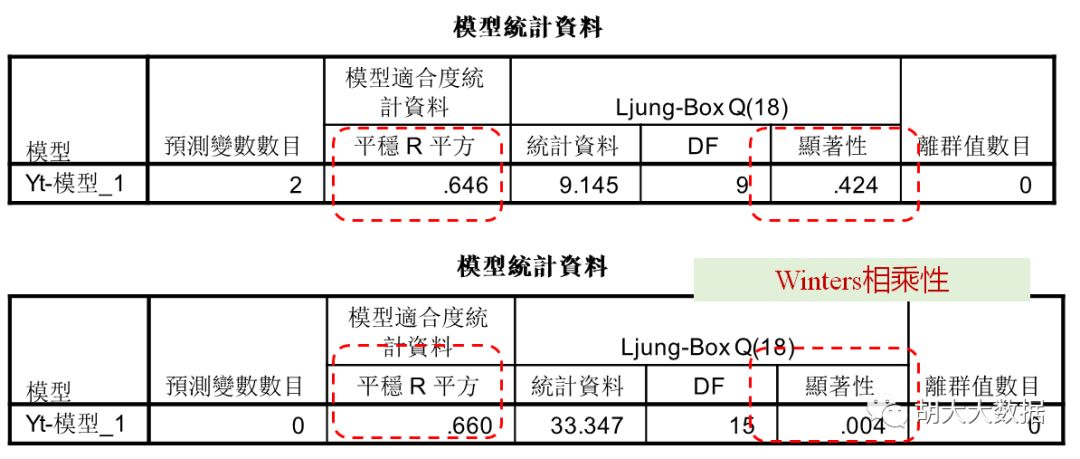
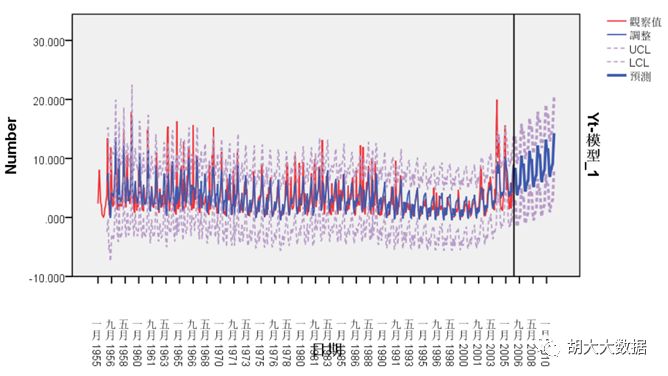
ARIMA(2,1,5)(1,1,1)回归效果与预测结果

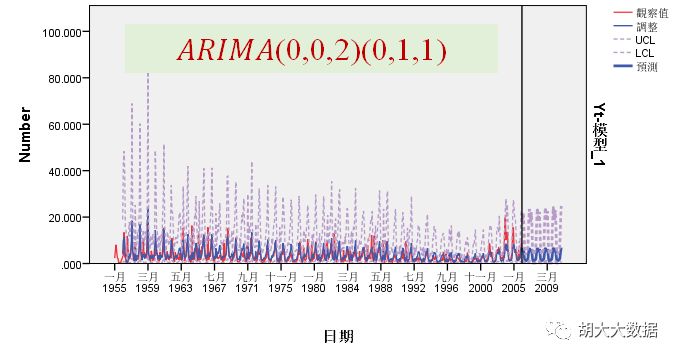
ARIMA(0,0,2)(0,1,1)回归效果与预测结果

Winters相乘性模型回归效果与预测结果