时间序列预测模型ARIMA浅析

Posted 2021-05-02 机器学习blog

本文聊聊arima模型。

ARIMA是一种比较常用的基于历史数据来做预测的时间序列模型。时间序列在商业中有很多应用，比如它可以解释销售中的季节性规律；可以预测新客或流失客户的数量等。

本文以R为例来介绍arima模型。

ARIMA的全称是auto-regressive integrated moving average，主要是由三个参数确定的，即(p,d,q)。其中auto regressive (AR(p)) 是指回归过程中某个时间点的取值依赖于过去的p个时间点的取值。比如，AR(5)或者ARIMA(5,0,0)就表示当前取值依赖于过去的5个时间点的取值。参数d表示差分 I(d) 的阶，差分即为用当前的值减去之前的值。差分主要用于将不平稳的序列平稳化。moving average MA(q) 表示模型的的误差是之前误差的组合。阶数q表示当前的误差依赖于之前q个误差。这三个成分使得ARIMA模型不具有季节性，可以写成线性方程。

应用模型之前首先要对原始数据有个概括性的认识。可以画出这些数据，观察其中的规律以及异常情况，然后处理异常值或缺失值，R语言中的 tsclean() 函数可以比较好的处理异常值以及缺失值。如果原始数据具有比较陡峭的增长趋势，比较建议对整个序列对数化，即对数化。

对于时间序列类型的数据，一般都会有一定的趋势性或者季节性，R语言中的decompose() 或者 stl() 函数可以检测或者移除其中的趋势性。要检测时间序列是否是平稳的，可以利用函数 adf.test() 来检查。ACF，PACF这两个图有助于确定差分的阶数。时间序列中的残差应该是正态分布的，模型误差一般可以用AIC 或者 BIC 来衡量。

下面利用示例来讲解ARIMA。

首先加载依赖包，加载数据。

接下来，审查数据，观察其趋势，查看是否有异常值等等。

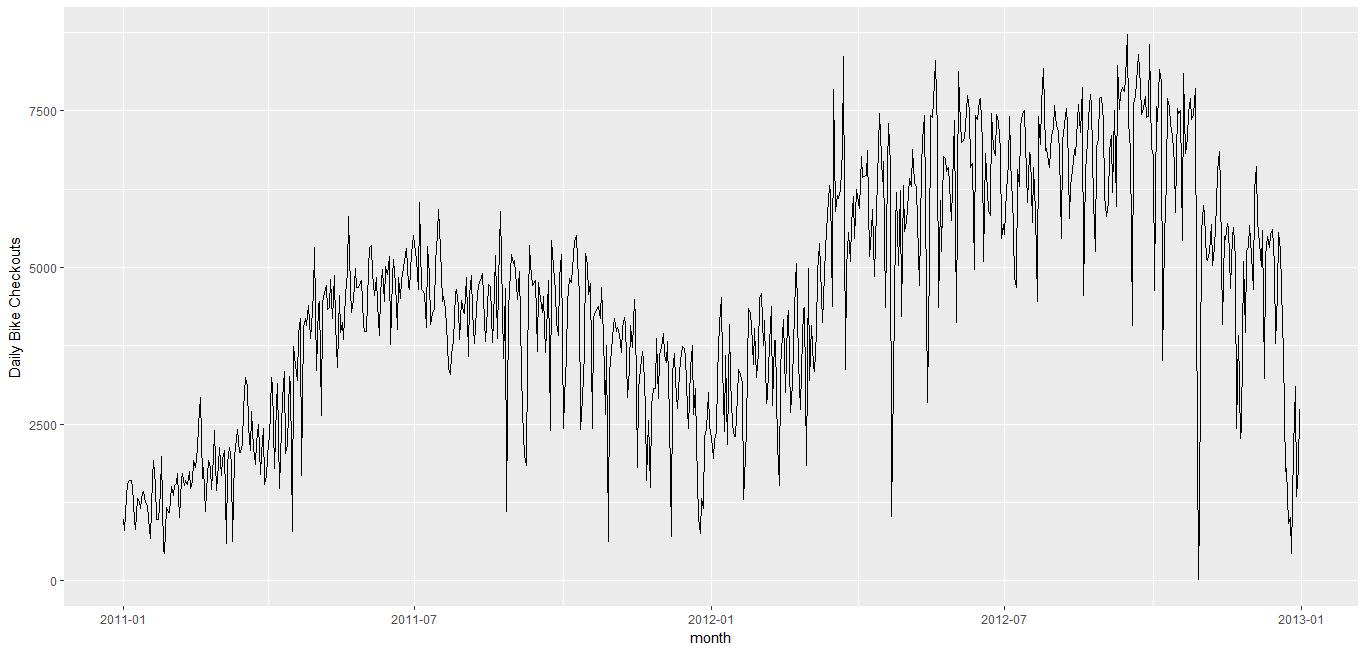
显然，该数据的波动挺大的，而且不同季节的幅度也有较大差别。也存在两天之间的数值跨越非常大，这种变化很有可能就是离群点。R语言中针对时间序列包含了去除离群点的函数， 比如 forecast 包里面的 tsclean()。这个函数不仅可以去除离群点，而且可以补充缺失值。 效果如下：

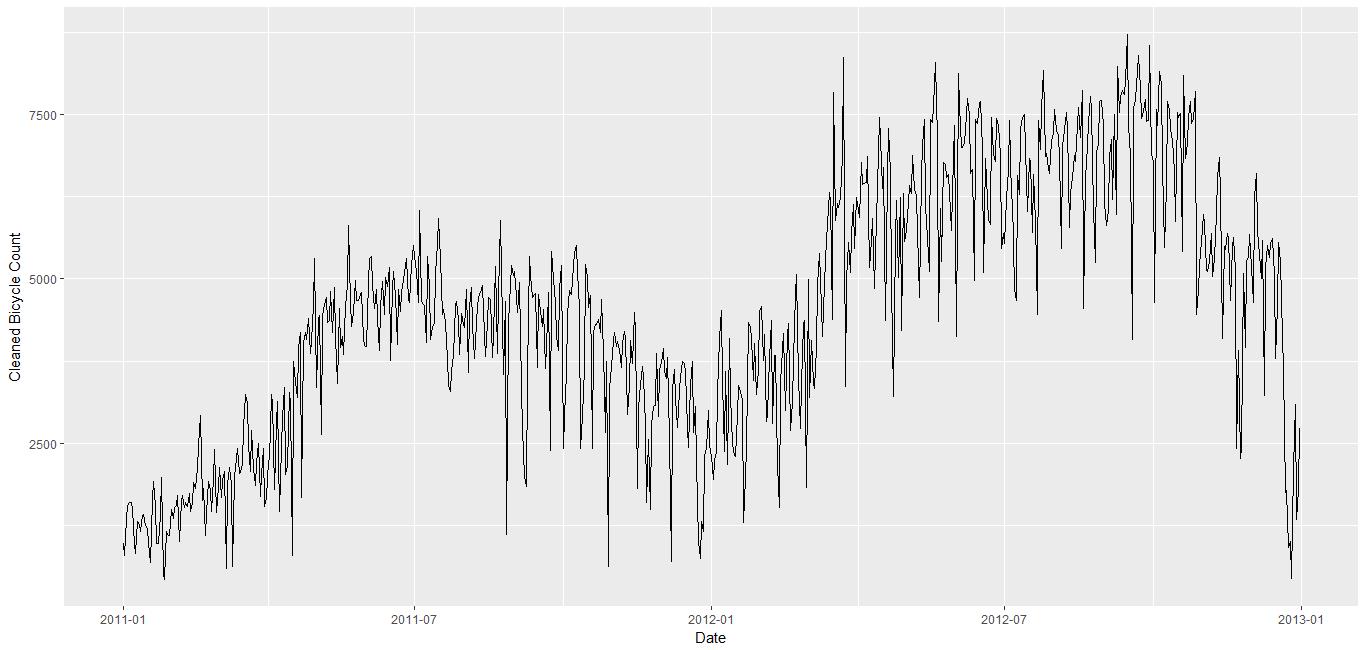
去除离群点之后，可以画一条线，保留其大致趋势，同时对噪声点光滑化。这就是时间序列中的移动平均。这种方法可以使得时间序列更加平稳可预测。移动平均的阶为k，则表示取出前后各k个样本点，然后取平均来代替原样本点。这是一般的移动平均，然而在ARIMA中的移动平均并不是对样本点的平均，而是对误差的平均。容易看出，移动平均的步幅越大，则该序列越平滑。

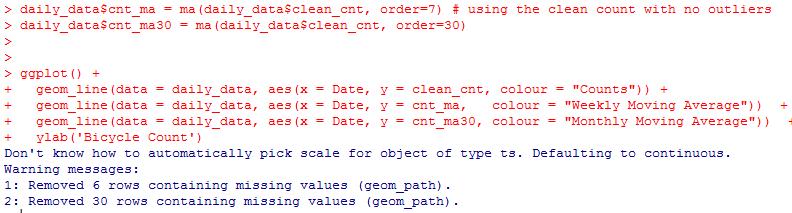
效果如下：

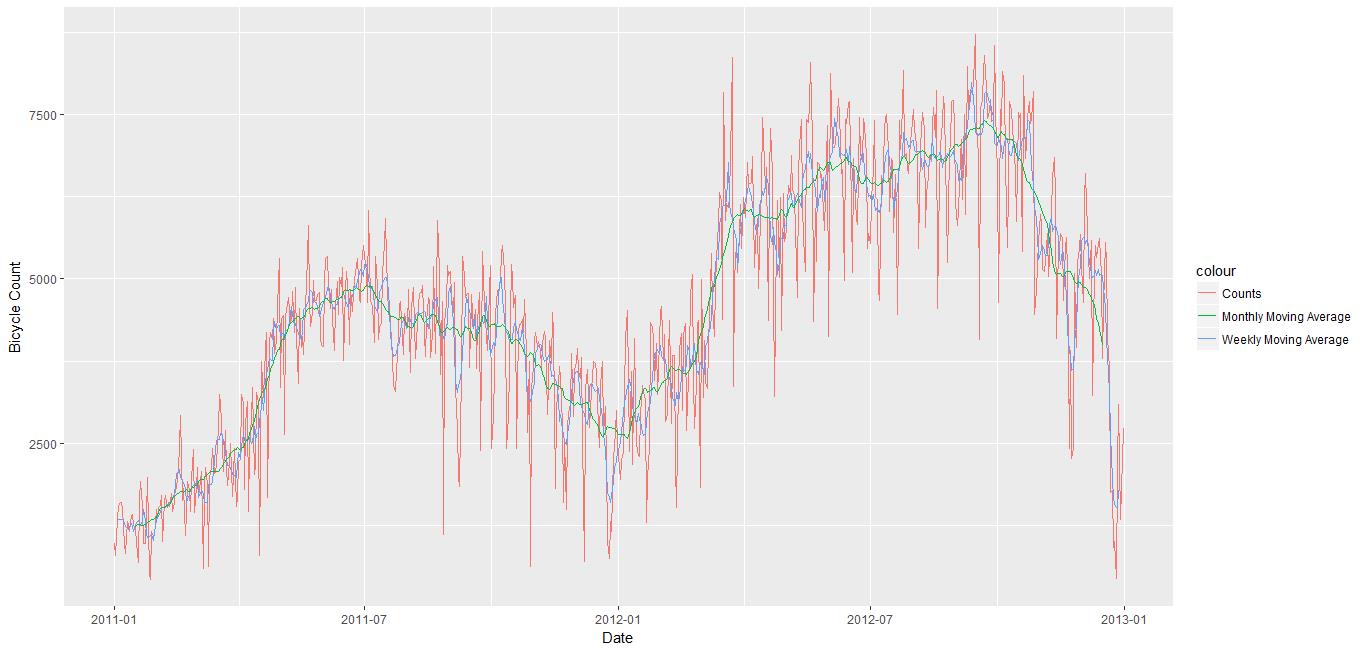
时间序列中三大构成包含了趋势性，季节性以及循环性。趋势性是指序列的整体变化趋势，比如是上升还是下降。季节性是指特定的时间段具有特定的特征，不同时间段的特征不一样。循环性是指周而复始的特性。通常趋势性和循环性是绑定在一起的。并不是所有的时间序列都具有这三个特性，但是，把这三个特征分离出来有利于构建预测模型。

季节性可以利用 stl() 来计算。这个函数可以将时间序列加以分解和预测，其中用到了平滑，并且从原始序列中将季节性分离出来。

示例如下：

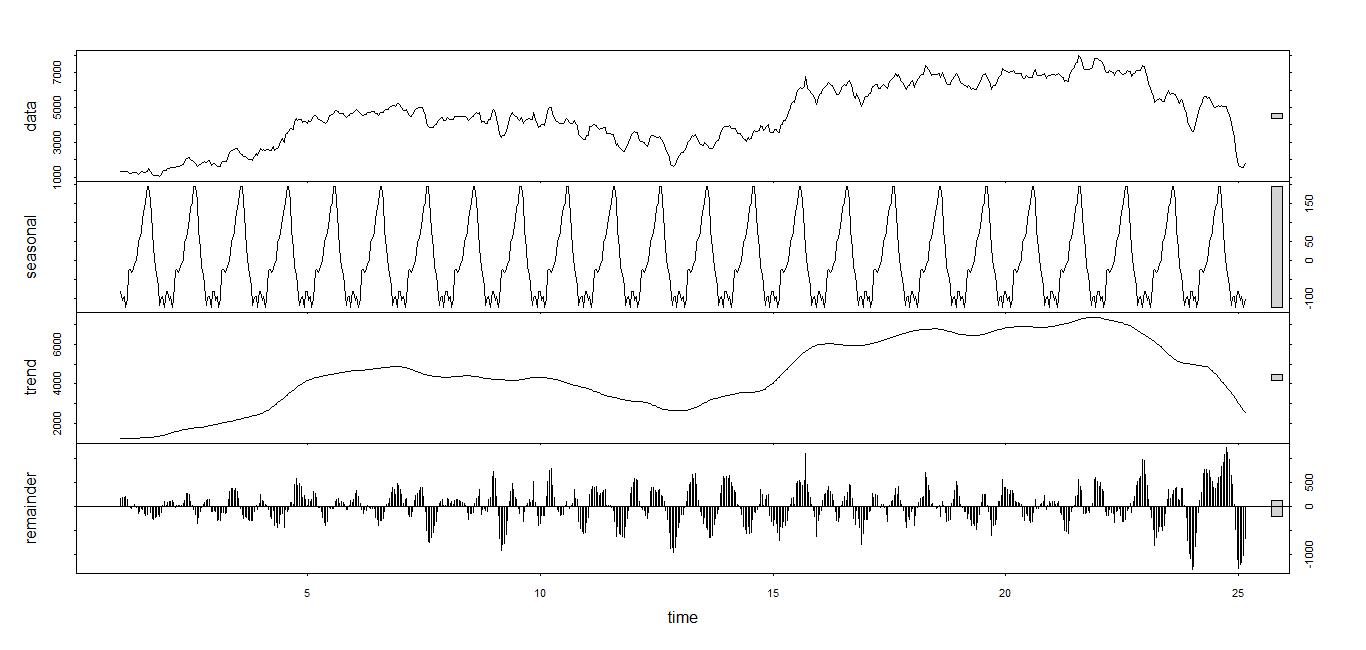
上面是分解成和式的，如果要分解成乘积，则需要设置  allow.multiplecative.trend=TRUE。

对ARIMA模型进行拟合，一般要求时间序列是平稳的，意即均值，方差以及自相关系数具有时间不变性。augmented Dickey-Fuller (ADF) 测试可以用来检验一个时间序列是否是平稳的。原假设是该序列是不平稳的。

示例如下：

容易看出，本例的原假设是成立的，即本例中的序列是不平稳的。

针对不平稳的时间序列，可以利用差分法进行校正。这种方法可以去除趋势性或者循环性。差分具有它的阶，一阶差分即为当前时间的取值减去前一时间点的取值。这种差分很容易扩展到二阶差分(d=2)，即为t时刻的取值减去t-1时刻的取值作为一个结果，然后再减去t-1时刻的取值减去t-2时刻的取值所得的差，公式上即为 (s_t-s_[t-1]) - (s_[t-1]-s_[t-2])。针对季节性的差分类似，差别在于季节的长短。

那么问题来了，如何选择差分的阶呢？ACF(autocorrelaion function) 在判断序列是否平稳时可以提供可视化界面，也可以选择ARIMA模型的阶。ACF可以帮助我们选择差分的阶，也有助于选择MA(q)的阶。Partial autocorrelation plots (PACF) 有助于选择AR(p)的阶。

示例如下：

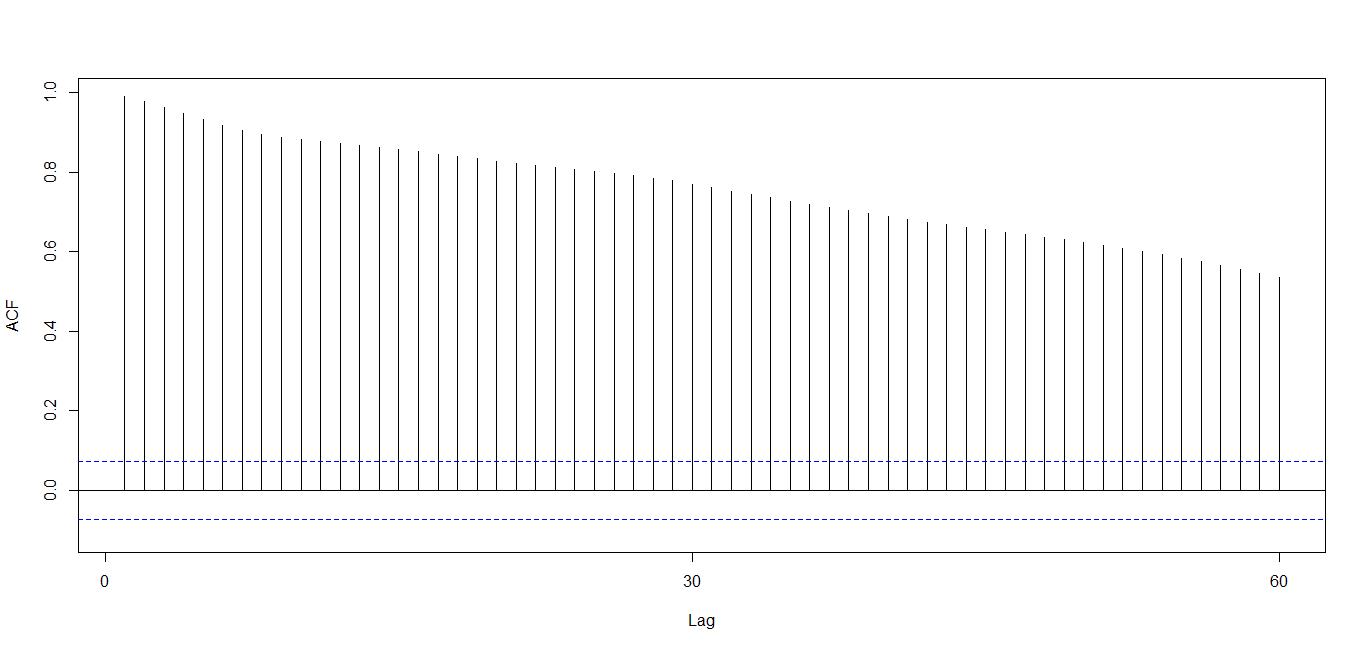
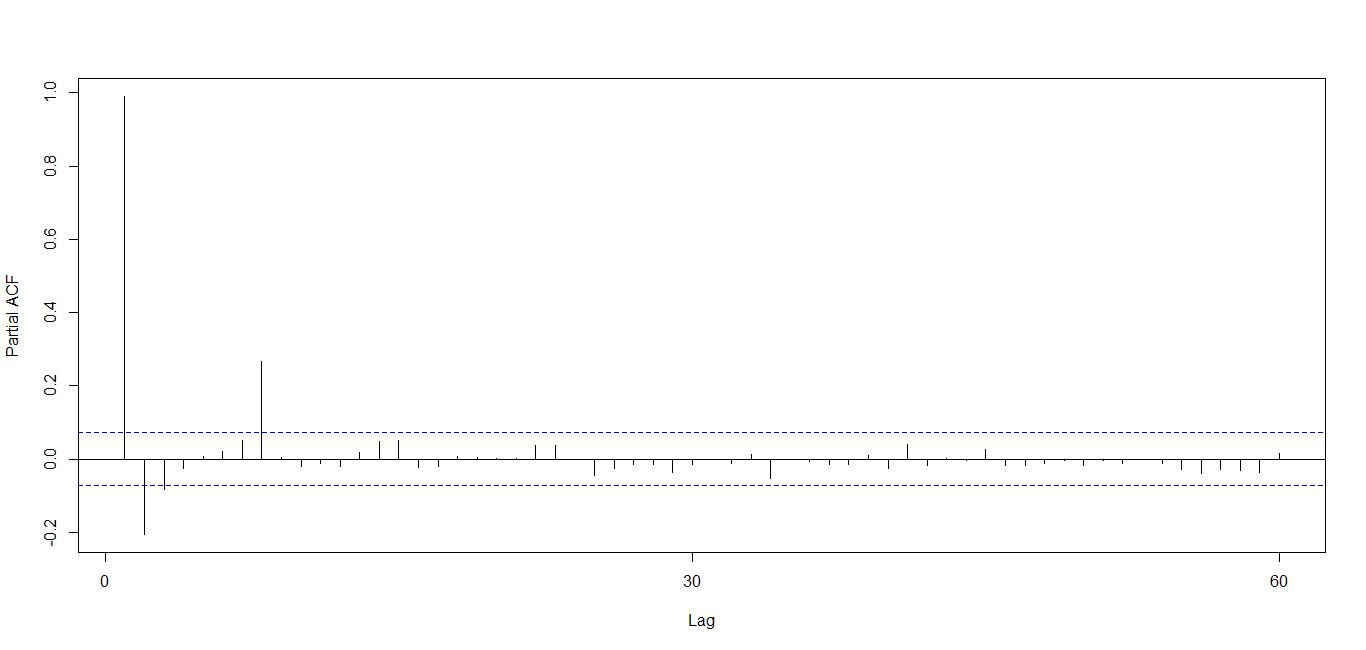
接下来从d=1开始选择合适的差分阶。利用ADF检验可以得到，一阶差分已经足够了，可以用于模型中。

示例代码如下：

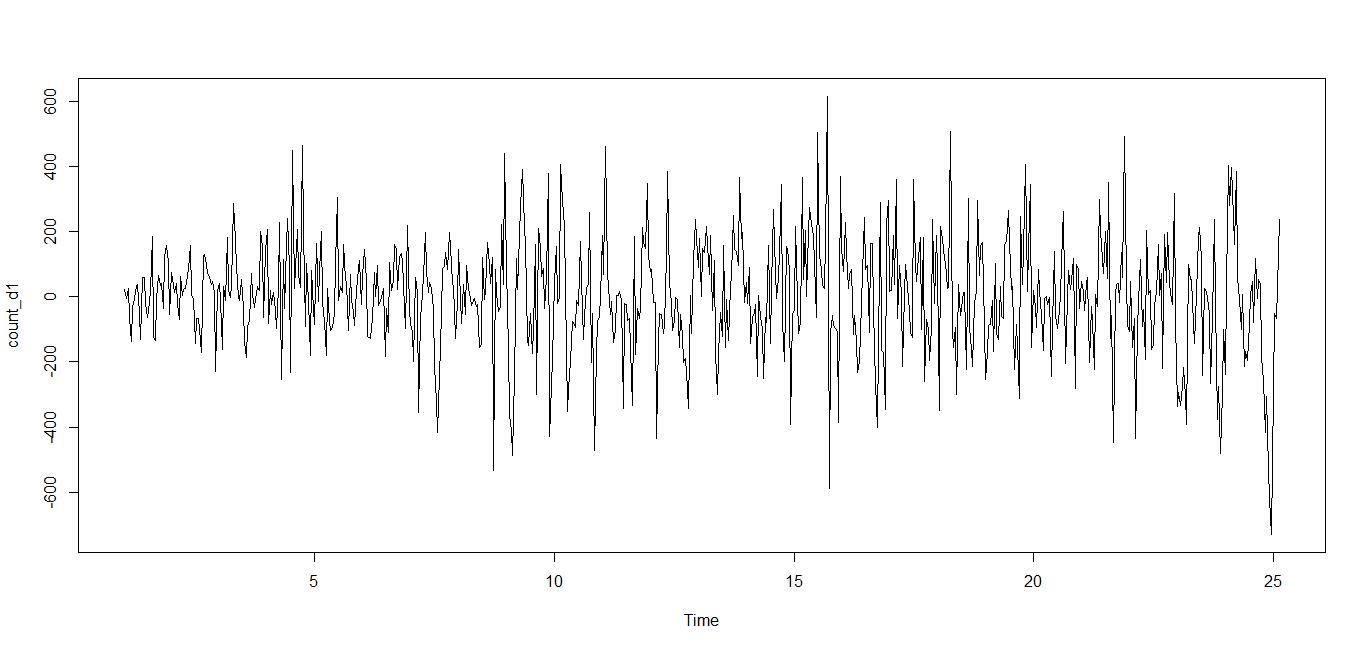
基于上面的差分序列可以进而确定p和q的取值。

示例代码如下：

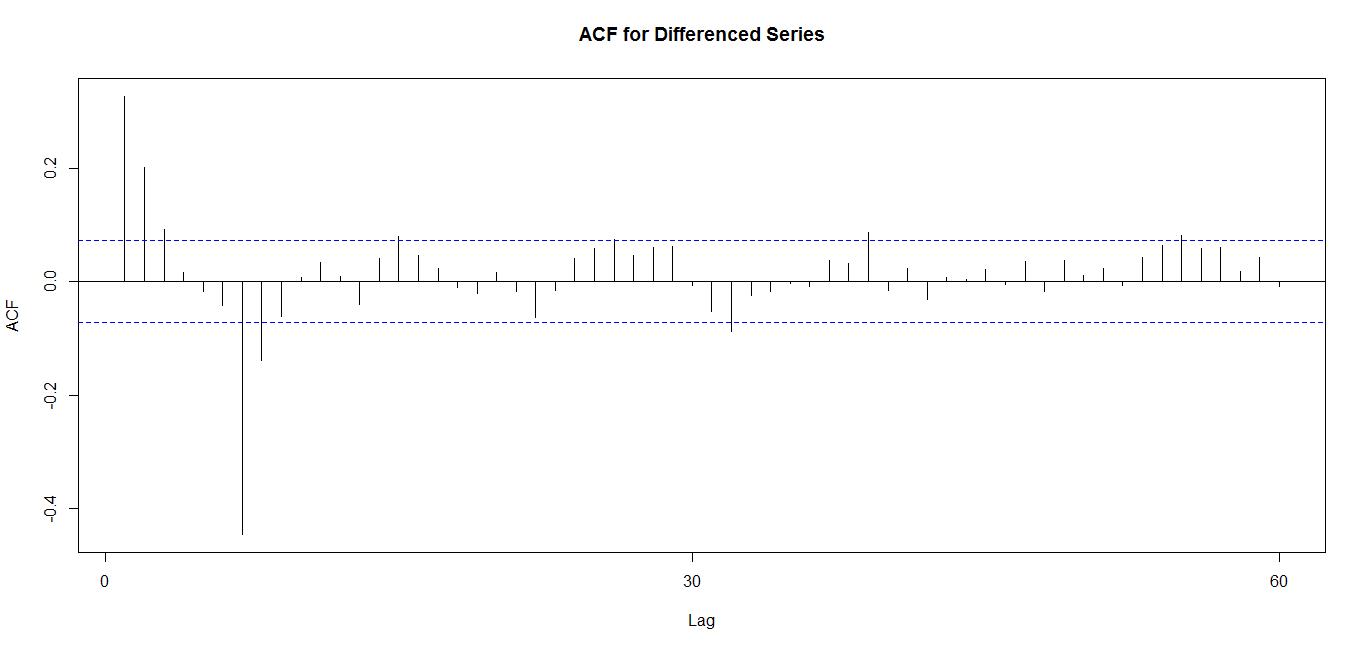
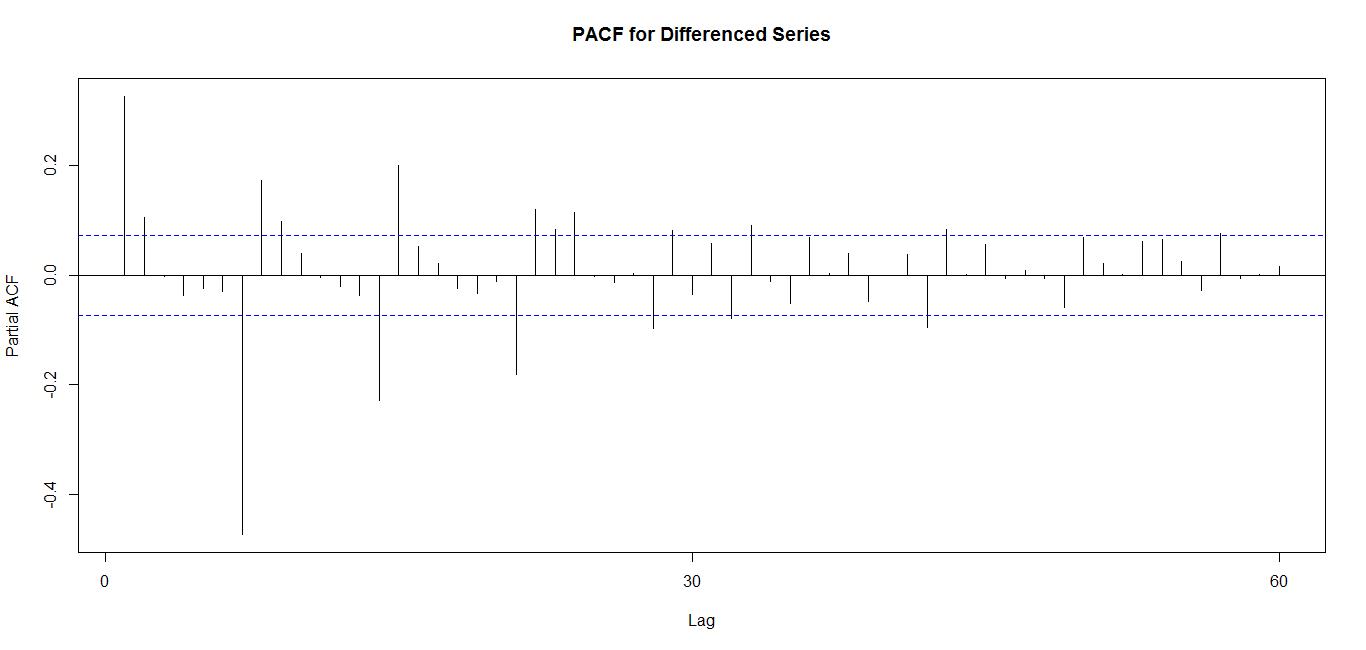
R语言的forecast包提供了用户自己指定阶的函数arima()，也提供了自动生成最佳(p,d,q)的函数auto.arima()。比较模型好坏的标准有很多，比较常用的两个即为Akaike information criteria (AIC) 和 Bayesian information criteria (BIC)。这些标准都是用来衡量丢失信息多少的，丢失信息越少越好，因此目标是最小化AIC和BIC。

可以根据上面的图选择参数(1,1,1)，即差分阶为1，自回归的阶为1，平滑移动的阶为1.。

示例代码如下：

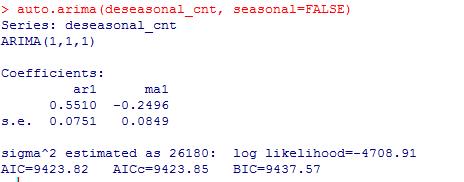
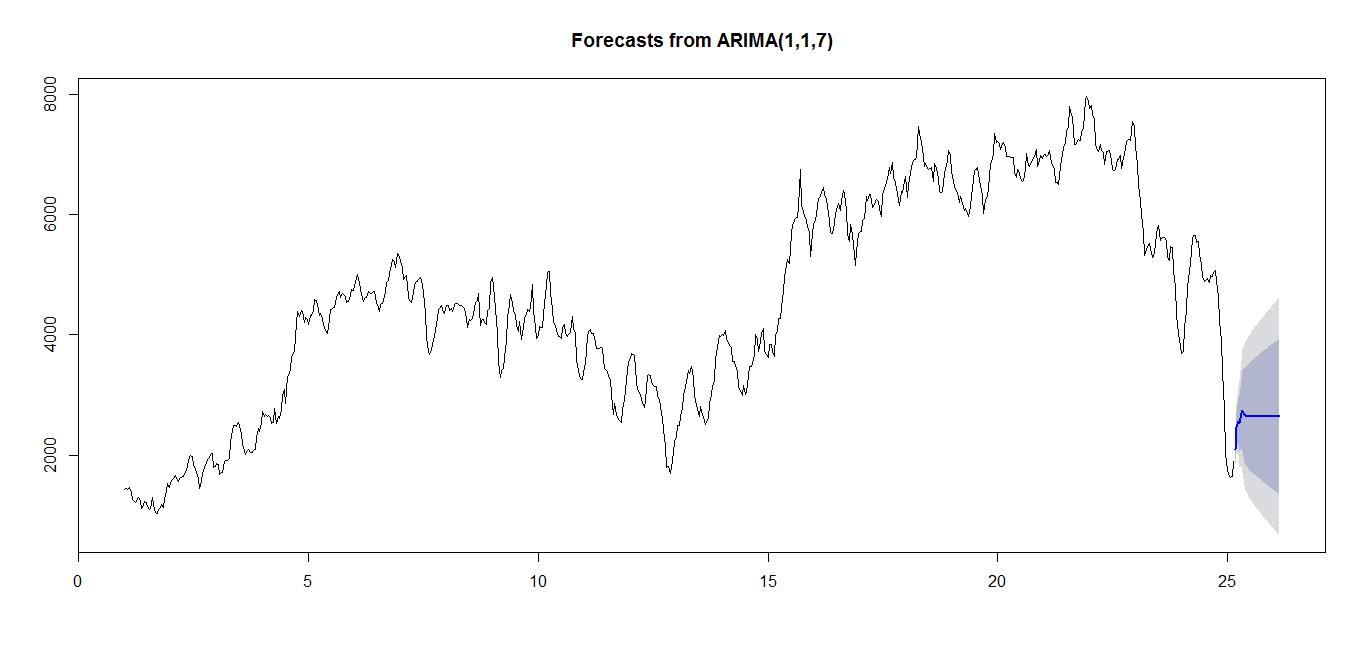
如果令q=7，则

容易发现AIC也很小。

然后就可以预测未来的序列取值，比如：

上面的例子中没有跟真实数据做对比，为了跟真实数据作对比，可以将真实数据抽取出来，然后作对比。比如：

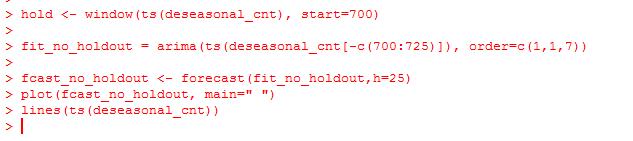
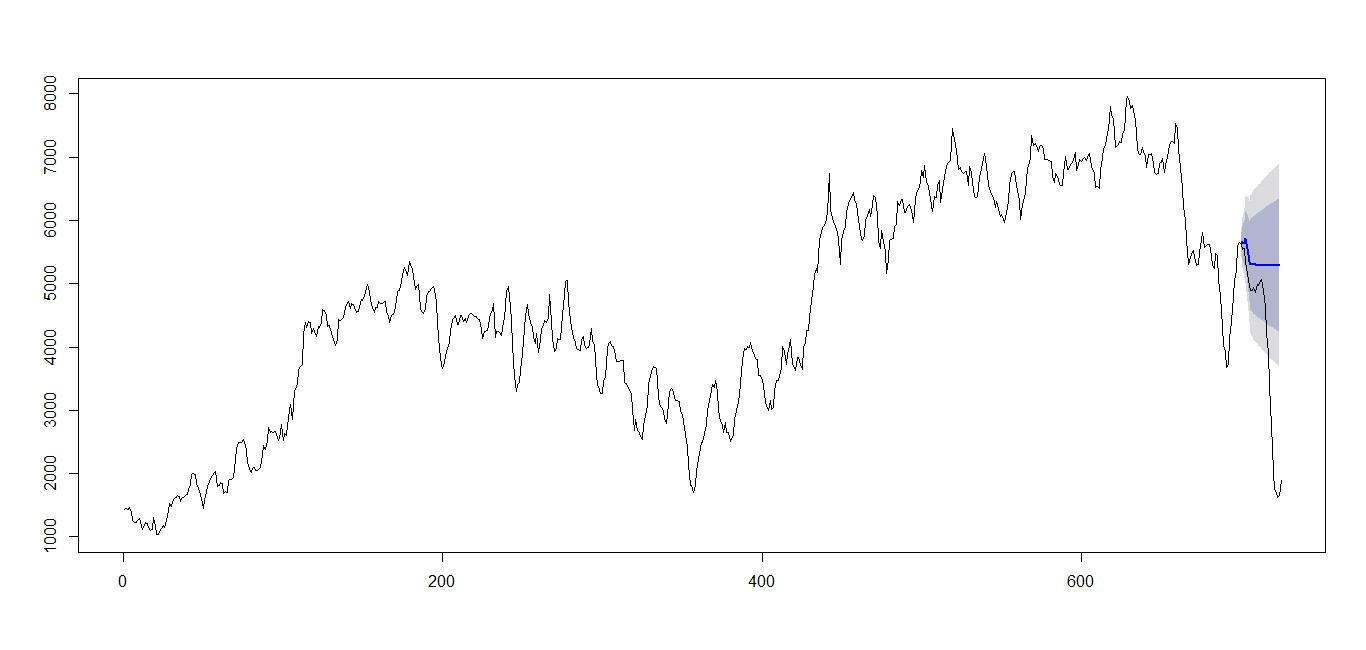
容易看出效果不好，主要原因在于没考虑季节性因素。为了提升效果，可以将季节性因素加入进来。

代码如下：

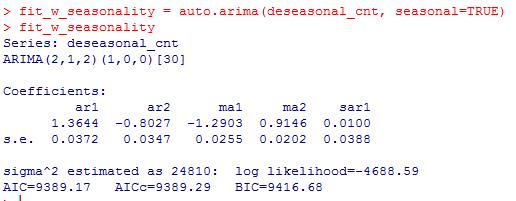
然后预测并画图：

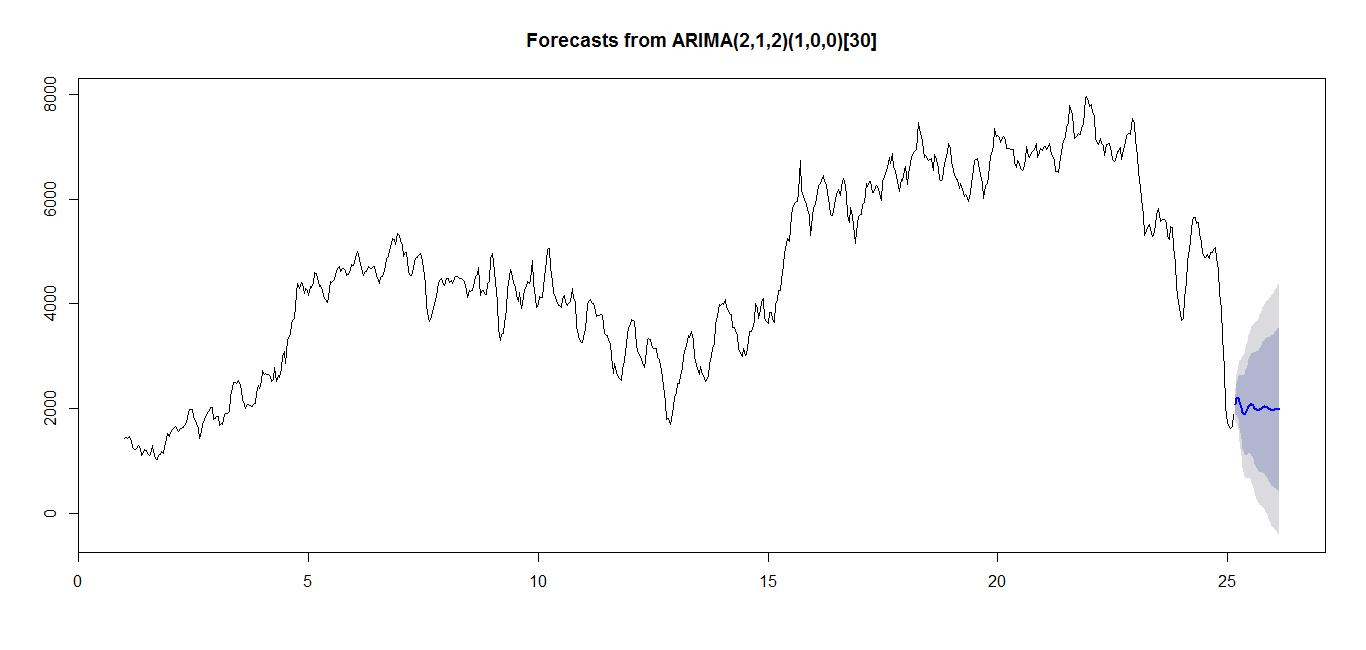
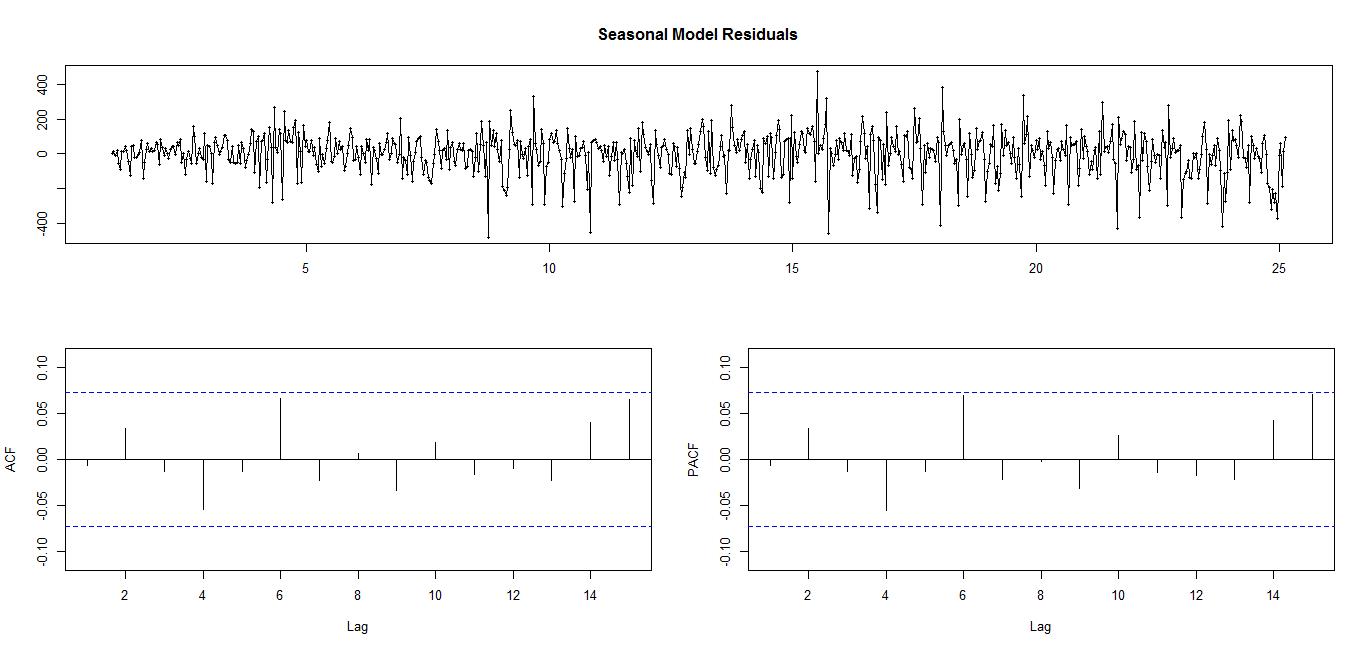
查看残差以及ACF，PACF的代码如下：

参考资料：

Fanaee-T, Hadi, and Gama, Joao, 'Event labeling combining ensemble detectors and background knowledge', Progress in Artificial Intelligence (2013): pp. 1-15, Springer Berlin Heidelberg, [http://link.springer.com/article/10.1007/s13748-013-0040-3].

Lichman, M. (2013). UCI Machine Learning Repository [http://archive.ics.uci.edu/ml]. Irvine, CA: University of California, School of Information and Computer Science.

https://www.datascience.com/learn-data-science/tutorials/introduction-to-forecasting-with-arima-r-data-science