线性结构

Posted 2022-11-27 天“码”行空

数据结构包括数据逻辑结构，数据存储结构，以及实现数据操作的算法。

在数据的逻辑结构中，有种常见的而且简单的结构叫做线性结构，即数据元素之间构成一个有序的序列。这一章，我们就来学习线性结构。

下面以一个例子为例，来引入线性结构：

【例1】

一元多项式及其运算

一元多项式的标准表达式可以表示为：f(x) = a0 + a1x^1+......+a(n-1)x^n-1+a(n)x^n

其运算有相加，相减，相乘

如何在计算机中表示一元多项式并实现其运算呢？

我们来看看一元多项式的标准形式：你会发现如果我们能够在计算机中存储一元多项式的项数n，以及每一项的系数a(i)，如a0,a1,.....a(n-1),a(n)，那么就意味着能够在计算机中来表示一元多项式了。

想想看，有几种方法呢？

方法一：采用顺序存储结构直接表示一元多项式

用一个数组a存储多项式的相关数据：数组分量a[i]表示项x^i的系数a(i), 即用数组分量下标对应于相应项的系数，而数组分量值就是系数。

例如f(x1) = 4x^5-3x^2+1可以用下表的数组表示：

下标i	0	1	2	3	4	5
a[i]	1	0	-3	0	0	4

现在用这种方法表示后，假设现在要进行多项式的运算。比如要实现两个多项式相加，应该怎么做呢？假设f(x2) = 3x^5+5x^3+2，求f(x1) + f(x2)的值？只需要把同下标下相应的系数相加即可。

下标i	0	1	2	3	4	5
b[i]	2	0	0	5	0	3

即把同i下，a[i]的值与b[i]的值相加即可，假设相加后得到一个新的值c[i],c[i]就是新多项式的系数数组。即要实现两个多项式相加，只要把两个数组对应分量项相加即可。

那这个方法有没有什么缺陷呢？

我们说，若多项式在比较稀疏（多项式有很高的阶，但只有很少的非零项）的情况下，时间和空间效率会很差。比如表示1+2x^30000这样的多项式，就必须采用一个大小至少30001的数组，而这个数组中大部分数据为0，只有两项不为0，显然空间浪费很厉害。而如果将之与多项式x+3x^2000加在一起，则必须遍历30001+2001个数组元素，可见，时间效率也很低。

那对于这种问题，有没有什么改进方法呢？比如说，能不能只存储非零项的信息，其它项就不必为他浪费空间了。来看下一种方法。

方法2：采用顺序存储结构表示多项式的非零项。

每个非零项a(i)x^i涉及两个信息：指数i和系数a(i)。因此可以将一个多项式看作是一个（a(i), i）二元组的集合。为了以后多项式运算方便，我们可以按照指数下降的顺序来组织这个二元组。所以可以把多项式看成是（a(i), i）二元组的有序序列（an,n）， （an-1, n-1）， ...... (a0, 0)。

我们可以用一个结构数组来存储以上系数非零项二元组的有序序列。数组的大小通过非零项的最多个数来确定，而不是通过多项式的阶数来确定。显然，这样做，相比于第一种方法，对于稀疏多项式的情况能节省大量空间。但是如果说多项式不是很稀疏，那么优势就没有了，甚至需要更多的空间。

现在有两个多项式，P（x1） = 9x^12 + 15x^8 + 3x^2和P（x2）= 26x^19 - 4x^8 - 13x^6 + 82

数组下标i	0	1	2
系数	9	15	3
指数	12	8	2

 

数组下标i	0	1	2	3
系数	26	-4	-13	82
指数	19	8	6	0

当多项式采用方法2时，相应的运算实现（如多项式相加）显然就比方法1复杂。因为方法1中，指数项相同的项的系数均有相同的数组下标，我们只需要把两个数组相同数组下标的数组元素的值相加即可。但是方法2中，数组下标相同，它们的指数不同，显然不能像数组1那样直接相加那么简单了。所以说，其计算比方法1复杂一些。

例如实现两个多项式的相加，可采用以下策略：分别从头开始查看两个多项式中的每一项，如果当前两项的指数不一样，那就将指数大的那一项“拷贝”到结果多项式中；如果它们指数一样，而且对应系数和不为0，那么就在多项式中增加一个系数作为它们之和的新项。

对于图3.2中的例子，这两个多项式的相加过程基本是这样：

【1】比较（9，12）和（26，19），将（26，19）移到结果多项式；

【2】比较（9，12）和（-4，8），将（9，12）移到结果多项式；

【3】比较（15，8）和（-4，8），将（11，8）增加到结果多项式；

【4】比较（3，2）和（-13，6），将（-13，6）移到结果多项式；

【5】比较（3，2）和（82，0），将（3，2）移到结果多项式；

【6】将（82，0）直接移到结果多项式。

最后得到的结果多项式是（（26，19），（9，12），（11，8），（-13，6），（3，2）），即多项式：

P（x）= 26x^19 + 9x^12 + 11x^8 - 13x^6 + 3x^2

这个方法有什么缺点呢？

用数组表示的一个问题是灵活性不够。由于事先无法知道多项式可能的非零项数，我们只能根据可能的最大值事先确定数组大小。有没有更好的方法呢？链表是一种更好的存储方法。

方法3：采用链表结构来存储多项式的非零项。

用链表表示多项式，每个链表的结点存储多项式的一个非零项，包括系数和指数两个数据域以及一个指针域，其结点结构可表示为：

Coef（系数）

Expon（指数）

Next（指针域）

 

 

对应的数据结构定义为：

struct PolyNode

   int Cofe;
   int Expon;
   struct PolyNode *Next;
;

如果要实现链表表示的两个多项式相加，采用的方法与结构数组的方法非常相似。

小结：

数据结构的操作与数据结构的存储方式密切相关。不同的数据存储方式，相应的操作实现方法是不一样的。比如用数组直接存储，多项式的加法运算通过简单的数组相加就可以实现。如果采用链表来记录非零项，那么多项式的相加运算要复杂的多。这两种方式比较起来，在多项式非零项相对少的情况下，前者实现简单，但时间和空间浪费大。后者实现起来复杂，但时间和空间效率高。所以数据结构的设计往往需要在算法的可理解性，时间，空间效率之间做折中，针对具体问题选择合适的数据结构和相应的算法。

例2.前面我们分析了一元多项式的表示，更进一步地，二元多项式该如何表示呢？比如给定二元多项式9x^12y^2 + 4x^12 + 15x^8y^3 - x^8y + 3x^2。

可以扩展一元多项式的表示方法来表示二元多项式，即我们可以把二元多项式按照一元多项式的方法来组织。比如可以将上述二元多项式看成x的一元多项式：

（9y^2+4）x^12 + （15y^3-y）x^8 + 3x^2。其中，一元多项式的常量系数在这里就成了y的一元多项式。同样，我们可以采用链表结点表示多项式的各个非零项，原来结点中表示链表系数的域就成了指向关于y的一元多项式链表的指针域（存放地址）。

上述二元多项式可用如下链表表示：

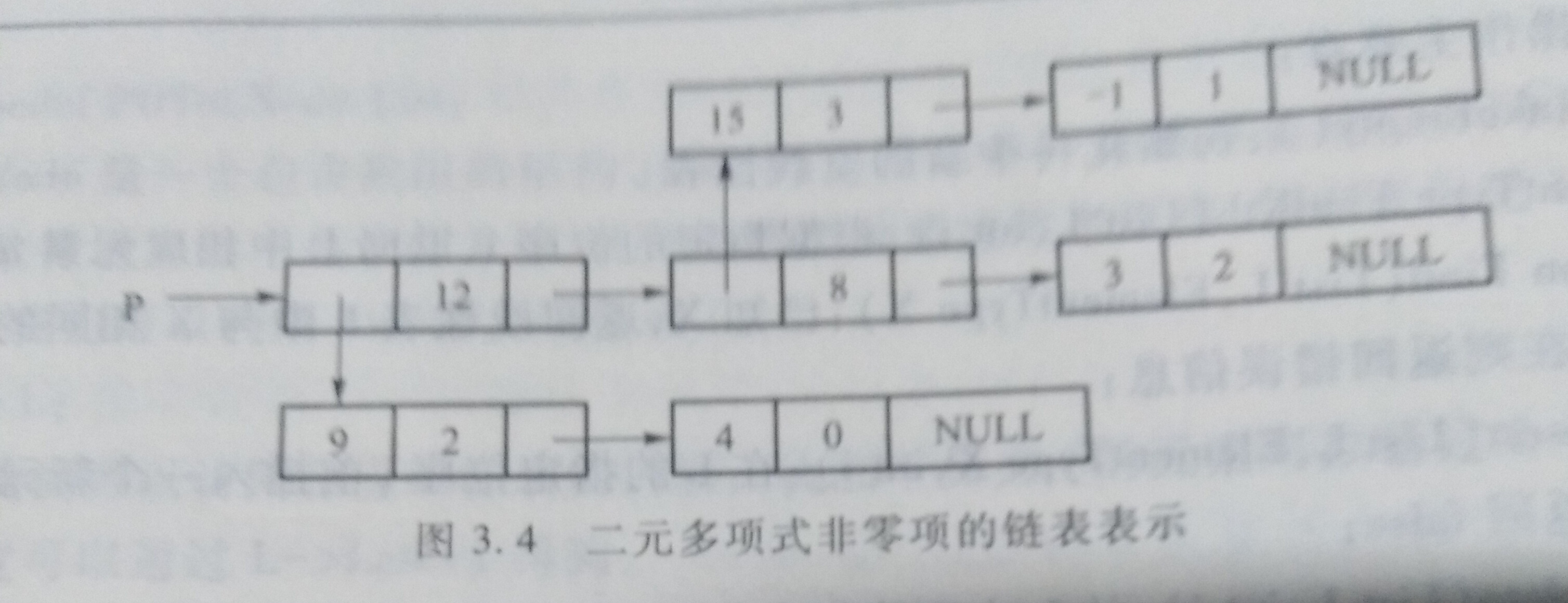
上述二元多项式是按照x的指数组织的一个有序序列。在该序列中，即包含纯粹的“（系数，指数）项”，也有包含一元多项式（当然也是有序序列的项）。类似这种包含子序列的有序序列就是一种广义表。

在前面的多项式的例子中，我们将多项式问题抽象为由系数和指数所构成的二元组有序序列的存储与操作问题。我们可以研究更为一般的有序的对象序列的组织和管理方法，其操作包括：插入元素，删除元素等。这问题就是下面要学习的线性表，也是一类典型的数据结构。

 

 

关注即可和我继续学习接下来的内容哦！ ！我们一起学习，一起进步，我会持续更新的。。。。。。