区块链与密码学第6-2讲：经典数字签名算法—RSA数字签名算法

Posted 2022-04-27 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

6.2 RSA数字签名法

数字签名一般利用公钥密码技术来实现，其中私钥用来签名，公钥用来验证签名。比较典型的数字签名方案有：

RSA签名算法(R. L. Rivest, A. Shamir, and L. M. Adleman, 1978) 

ElGamal 签名算法(T. ElGamal, 1985) 

Schnorr签名算法(C. P. Schnorr, 1989) 

DSS签名算法(NIST, 1991)

基于RSA公钥体制的签名方案通常称为RSA数字签名方案。RSA签名体制的基本算法如下：

密钥的生成（与加密系统一样）：

公钥Pk=e,n；私钥Sk=d

签名过程（d,n）:

用户A对消息M∈Zn进行签名，计算：

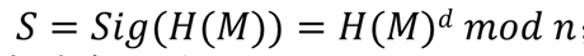
并将S附在消息M后

验证过程（e,n）:

给定（M,S），Ver（M,S）为真，则H(M)=Se(mod n)成立

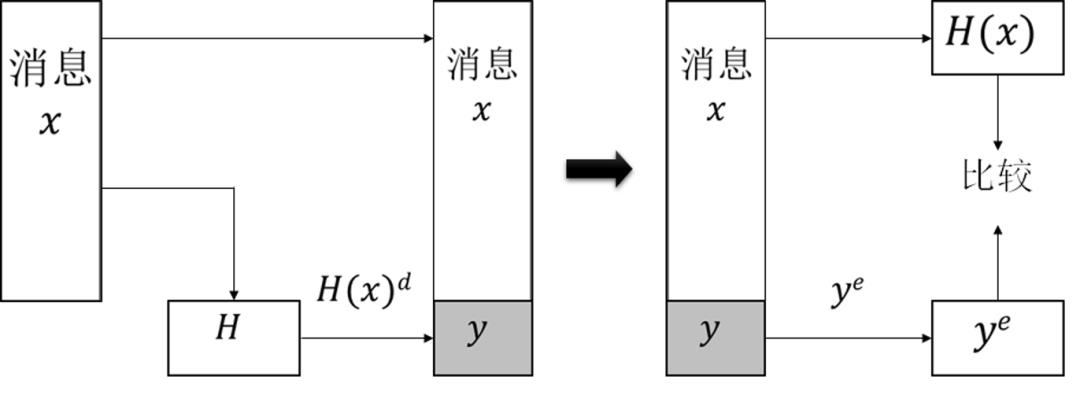
RSA数字签名算法工作流程

假设RSA直接对消息进行签名

一般攻击：攻击者任选一个数据Y,用A的公钥计算X=Yemodn,于是便可以用Y伪造A对消息X的签名，因为：

实际意义不大：伪造的消息X具有实际意义的概率很小

Hash函数可以抵御这种攻击

利用已有签名进行攻击：如果消息M1、M2的签名分别是S1和S2，则任何知道M1,S1,M2,S2的人可以伪造对消息M1M2的签名S1S2因为

用户不要轻易对其他用户提供的随机数据进行签名

更有效的方法：对数据的Hash值签名

利用签名获得明文：攻击者截获密文C=Memod n,选择随机数r，并计算：

然后攻击者设法让发送者对y签名，获得：

攻击者计算：

用户不要轻易对其他用户提供的随机数据进行签名

更有效的方法：对数据的Hash值签名

H(M)的另一个作用一加快签名速度

对整个消息签名，由于公钥体制速度比较慢，当消息比较长时，签名与验证过程都会相当慢

对消息的Hash值签名，则无论消息多长，签名都只与Hash值的长度有关

RSA算法比较慢，用私钥进行签名和公钥进行验证。因上述RSA签名算法沒有加入随机数，当出现重复性的原始资料，攻击者会通过相同签名信息而猜测出原文。应该怎么办呢？

PSS (Probabilistic Signature Scheme)私钥签名流程的一种填充模式。

目前主流的RSA签名包括RSA-PSS和RSA-PKCS#1 V1.5。

后者相对应PKCS (Public Key Cryptography Standards)是一种能够自我恢复签名，而PSS无法从签名中恢复原来的签名。

OpenSSL-1.1.x以后默认使用更安全的PSS的RSA签名模式。

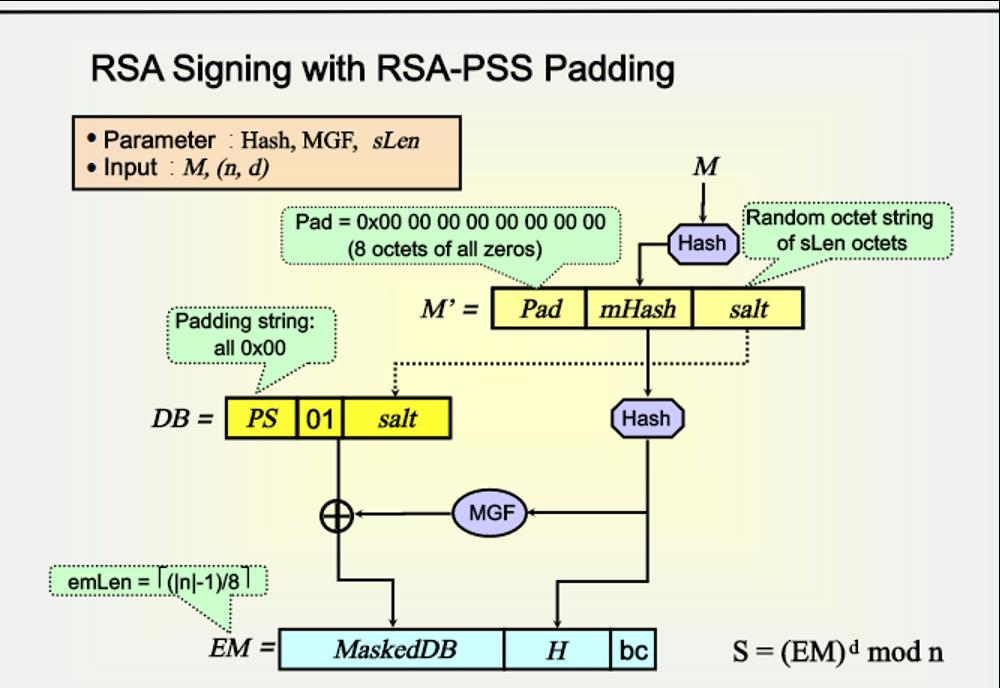
 PSS算法的编码操作过程

RSA-PSS数字签名算法

密钥生成

生成一个模数n，一个公钥e和一个私钥d。

假设安全参数为k(n是k比特的数)，我们定义两个整数k0和k1并且满足：k0+k1≤k-1

然后我们定义两个哈希函数：一个扩展数据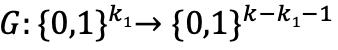

 

，一个压缩数据

签名算法

为了对一个消息m进行签名，签名者执行以下步骤：

① 生成一个随机数

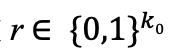
② 计算w=H(m||r)

③ 设置y=0||w||(G1(w)⊕r)||G2(w)

④ 计算s=ydmod n

⑤ 消息m的签名为s

验证算法

为了对一个消息m进行的签名s进行验证，验证者执行以下步骤：

① 计算y=semod n

② 将y分解成: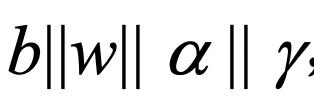

 ，其中b的长度为1比特，w的长度为k1比特，a的长度为k0比特，γ的长度为k-k0-k1-1比特

③ 计算r=a⊕G1(w)

④ 当且仅当下列等式成立时，接受该签名：

 

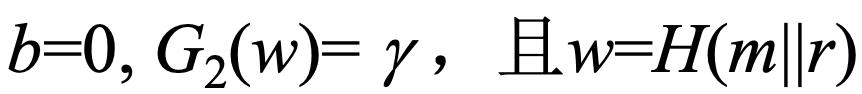
今天的课程就到这里啦，下一堂课我们将介绍经典的数字签名算法—ElGamal数字签名算法，带大家继续了解数字签名，敬请期待！

-- 完 --

关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集