区块链与密码学第6-3讲：数字签名算法大合集

Posted 2022-04-27 Dig Quant

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网，版权归属其原作者所有，如有侵权请立即与我们联系，我们将及时处理。】

6.3 其他数字签名算法

EIGamal算法

数字签名一般利用公钥密码技术来实现，其中私钥用来签名，公钥用来验证签名。ElGamal公钥密码算法是在密码协议中有着重要应用的一类公钥密码算法，其安全性是基于有限域上离散对数学问题的难解性。它至今仍是一个安全性良好的公钥密码算法。它既可用于加密又可用于数字签名的公钥密码体制。

假设p是一个大素数，g是GF(p)的生成元。Alice的公钥为y = gx mod p, g，p私钥为x。

签名算法：

Alice用H将消息m进行处理，得h=H(m).

Alice选择秘密随机数k，满足0<k< p-1，且(k, p-1)=1

计算r=gk (mod p)，s=(h－ x · r) · k-1(mod (p－1))

Alice将(m，r，s)发送给Bob

验证签名过程：

接收方收到M与其签名(r，s)后：

计算消息M的Hash值H(M)

验证公式

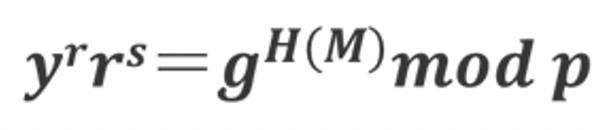
成立则确认为有效签名，否则认为签名是伪造的

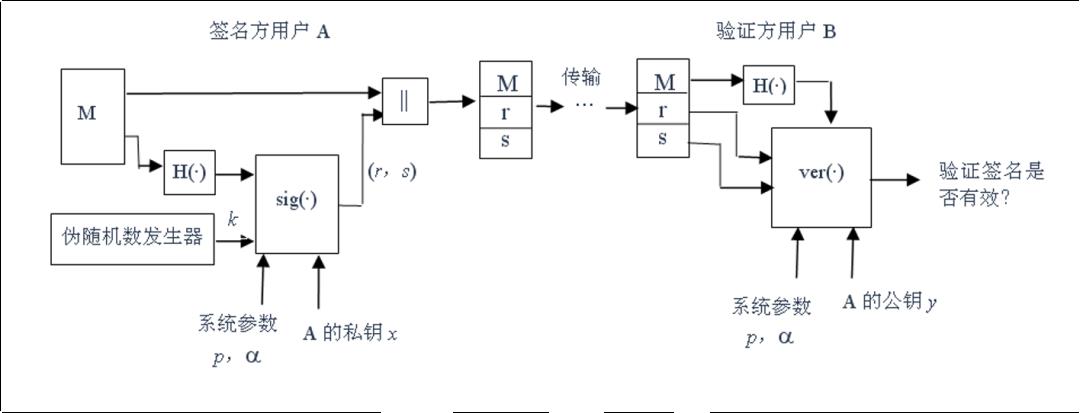
PSS算法的编码操作过程

上述方案的安全性是基于如下离散对数问题的：已知大素数p、GF(p的生成元g和非零元素y∈GF(p)，求解唯一的整数k, 0≤k≤p – 2，使得y≡gk (mod p)，k称为y对g的离散对数。

在1996年的欧洲密码学会(Proceedings of EUROCRYPT 96)上，David Pointcheval和Jacques Stern给出一个ElGamal签名的变体，并基于所谓分叉技术证明了在随机预言模型下所给方案是安全的(在自适应选择消息攻击下能抗击存在性伪造)。

Schnorr算法

Schnorr签名方案是一个短签名方案，它是ElGamal签名方案的变形，其安全性是基于离散对数困难性和哈希函数的单向性的。

假设p和q是大素数，是q能被p-1整除，q是大于等于160 bit的整数，p是大于等于512 bit的整数，保证GF(p)中求解离散对数困难；g是GF(p)中元素，且gq≡1mod p。

密钥生成： 

Alice选择随机数x为私钥，其中1<x<q； 

Alice计算公钥y≡gx (mod p)

签名算法：

①Alice首先随机数k，这里1<k<q； 

②Alice计算e=h(M, gk mod p)

③Alice计算s=k-x·e(mod q) 

④Alice输出签名(e, s) 

验证算法：

Bob计算gkmod p=gs·ye mod p 

Bob验证e = h(M, gk mod p)是否成立，如果成立则输出「Accept」，否则输出「Reject」。

Schnorr签名与ElGamal签名的不同点：

安全性比较：在ElGamal体制中，g为域GF(p)的本原元素；而在Schnorr体制中， g只是域GF(p)的阶为q的元素，而非本原元素。因此，虽然两者都是基于离散对数的困难性，然而ElGamal的离散对数阶为p-1， Schnorr的离散对数阶为q

签名长度比较：Schnorr比ElGamal签名长度短

ElGamal：(m，r，s)，其中r的长度为|p|， s的长度为|p-1|

Schnorr：(m，e，s)，其中e的长度为|q|， s的长度为|q|

DSA算法

1991年，美国政府颁布了数字签名标准(Digital Signature Standard, DSS)，也称为数字签名算法(Digital Signature Algorithm, DSA) 。

和DES一样，DSS也引起了激烈的争论，反对者认为：密钥太短、效率不如RSA高、不能实现数据加密并怀疑NIST在DSS中留有后门。

随后，美国政府对其做了一些改进，目前DSS的应用已经十分广泛，并被一些国际标准化组织采纳为国际标准。2000年，美国政府将RSA和椭圆曲线密码引入到数字签名标准中，进一步丰富了DSA算法。

DSA的主要参数：

全局公开密钥分量，可以为用户公用

p：素数，要求2L-1<p<2L,512<=L<1024，且L为64的倍数

q : (p-1)的素因子，2159<q<2160，即比特长度为160位

g : =h(p-1)/q mod p.其中h是一整数，1<h<(p-1)且üh(p-1)/q mod p>1

用户私有密钥

x：随机或伪随机整数，要求0<x<q

用户公开密钥

y：=gx mod p 

随机数k  

随机或伪随机整数，要求0<k<q 

DSA签名过程：

用户随机选取k

计算e=h(M)；

计算r=(gk mod p) mod q 

计算s=k-1(e+x · r) mod q

输出(r, s)，即为消息M的数字签名

DSA验证过程：

接收者收到M, r, s后，首先验证0<r<q, 0<s<q

计算e=h(M)； 

计算w=(s)-1 mod q  

计算u1=e · w mod q 

计算u2=r · w mod q

计算①v=[(gu1 · yu2) mod p] mod q

如果v=r，则确认签名正确，否则拒绝

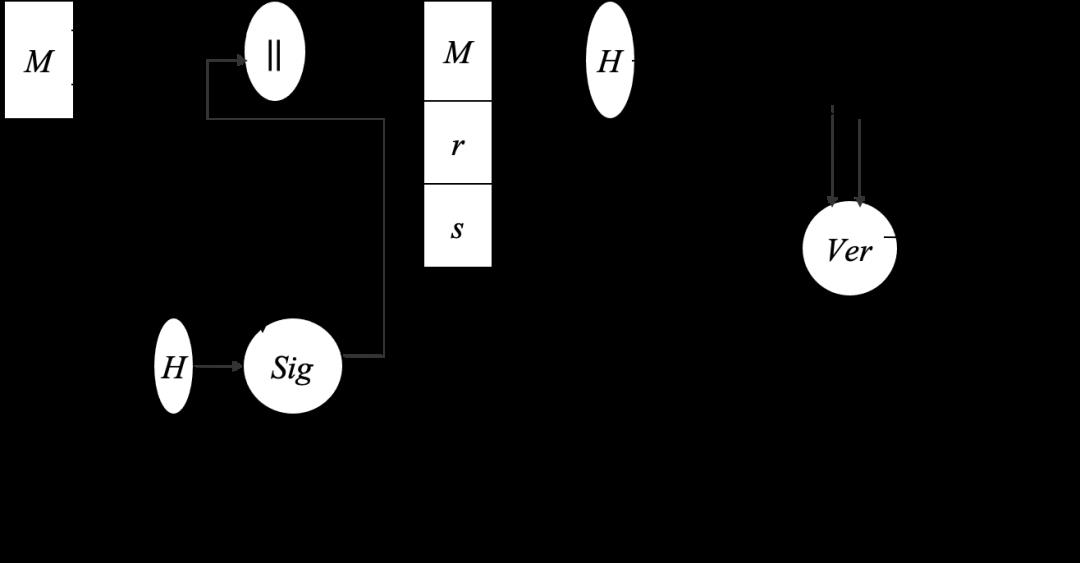
DSA算法的工作流程

今天的课程就到这里啦，下一堂课我们将学习基于椭圆曲线的数字签名算法，带大家继续了解数字签名，敬请期待！

-- 完 --

关注点宽学园，每周持续更新区块链系列课程，小宽带你进入区块链世界。我们下节课见啦。

【区块链与密码学】课堂回顾：

区块链与密码学系列文章合集