区块链与密码学第6-7讲:SM9数字签名算法
Posted Dig Quant
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了区块链与密码学第6-7讲:SM9数字签名算法相关的知识,希望对你有一定的参考价值。

【本课堂内容全部选编自PlatON首席密码学家、武汉大学国家网络安全学院教授、博士生导师何德彪教授的《区块链与密码学》授课讲义、教材及互联网,版权归属其原作者所有,如有侵权请立即与我们联系,我们将及时处理。】
6.7 SM9数字签名算法
为了降低公开密钥系统中密钥和证书管理的复杂性,以色列科学家、RSA算法发明人之一Adi Shamir在1984年提出了标识密码(Identity-Based Cryptography)的理念。
标识密码将用户的标识(如邮件地址、手机号码、QQ号码等)作为公钥,省略了交换数字证书和公钥过程,使得安全系统变得易于部署和管理,非常适合端对端离线安全通讯、云端数据加密、基于属性加密、基于策略加密的各种场合。
2008年标识密码算法正式获得国家密码管理局颁发的商密算法型号:SM9(商密九号算法),为我国标识密码技术的应用奠定了坚实的基础。
SM9是基于双线性对的标识密码算法,与SM2类似,包含四个部分:总则、数字签名算法、密钥交换协议以及密钥封装机制和公钥加密算法。在这些算法中使用了椭圆曲线上的对这一工具,不同于传统意义上的SM2算法,可以实现基于身份的密码体制,也就是公钥与用户的身份信息即标识相关,从而比传统意义上的公钥密码体制有许多优点,省去了证书管理等。
SM9算法不需要申请数字证书,适用于互联网各种新兴应用的安全保障,如基于云技术的密码服务、电子邮件安全、智能终端保护、物联网安全、云存储安全等等。这些安全应用可采用手机号码或邮件地址作为公钥,实现数据加密、身份认证、通话加密、通道加密等安全应用,并具有使用方便,易于部署的特点,从而开启了普及密码算法的大门。
在政府高度重视和市场迫切需求的双向驱动下,国密算法SM1—SM9应时而生。其中,SM9算法于2016年3月由国家密码管理局正式公布。
国产商用密码示意图
双线性对的概念
设q是一个大素数,G1和G2是阶为q的两个加法群(椭圆曲线上的群), GT是阶为q的乘法群,我们称映射e:G1×G2→GT为双线性映射(双线性对),如果它满足以下条件:
双线性性:任给P1∈ G1 , P2∈ G2和任意整数a, b∈Zq,e(a⋅P1, b⋅P2 ) = e(P1, P2 )ab。
非退化性:存在Q1∈G1 , Q2∈G2使得e(Q1, Q2 )≠。
可计算性:对于任意给定的Q1∈G1 , Q2∈G2 ,计算e(Q1, Q2 )是容易的。
如果G1=G2 ,则称e为对称双线性对,否则称e为非对称双线性对。目前在密码学中广泛应用的主要有Weil对、Tate对、Ate对、R-Ate对等。
SM9密码算法选用了安全性能好、运算速率高的R-Ate对。
系统参数生成
密钥生成中心(Key Generation Center, KGC)执行以下步骤生成系统参数和主私钥:
KGC生成随机数sk做为主私钥,这里0<sk<q-1
KGC计算系统公钥Ppub=sk ∙ P2;
KGC保存私钥sk, 公布系统公钥。
注意:
SM9算使用BN曲线,G1和G2分别是椭圆曲线E(Fp)和E()的加法群,GT是乘法群,群G2中元素尺寸是群G1中元素尺寸的2倍。
选择系统公钥为G2中的元素,那么就可以使得用户私钥和签名中一部分是G1中元素,降低了用户私钥和签名的尺寸。
用户私钥生成
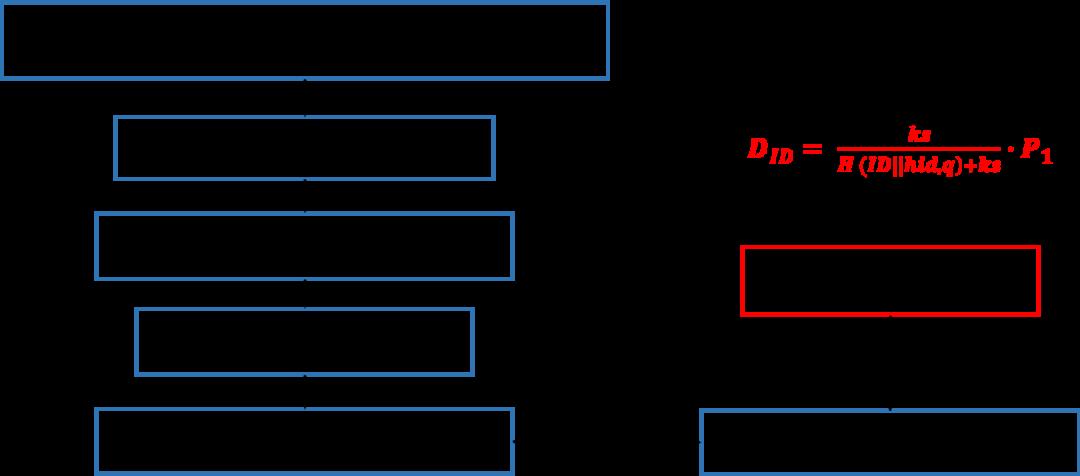
SM9数字签名算法用户私钥生成示意图
签名
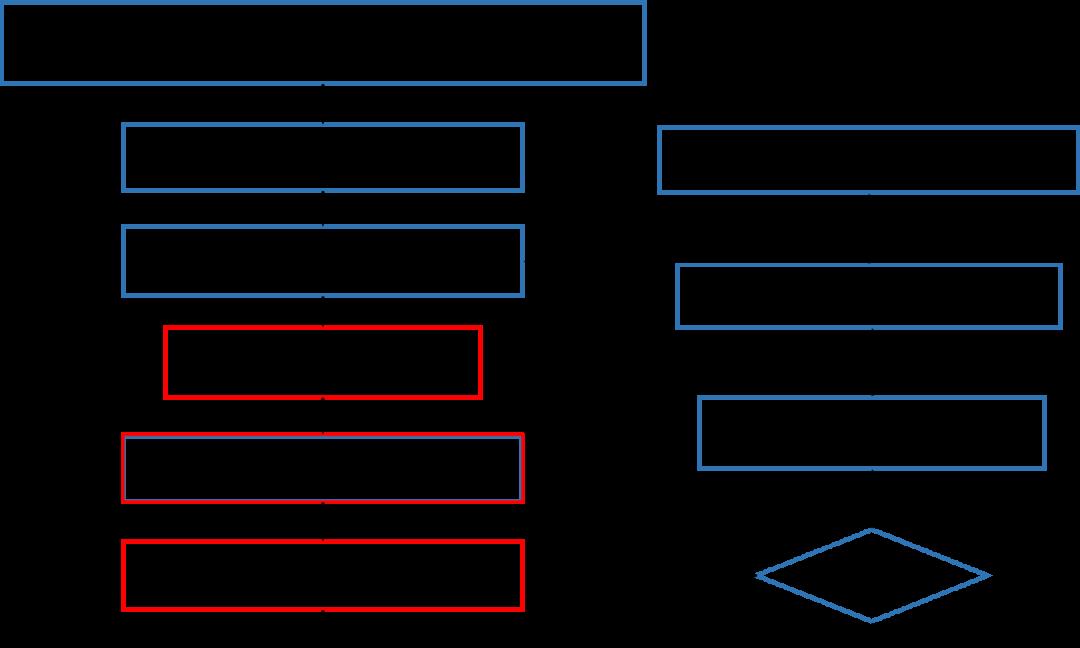 SM9数字签名算法签名过程示意图
SM9数字签名算法签名过程示意图
验证
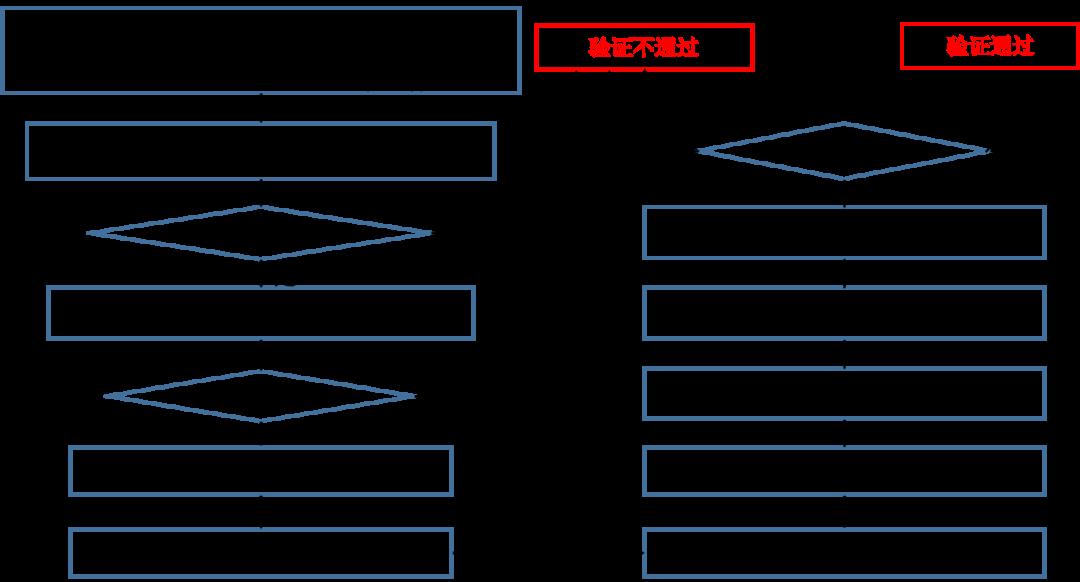
SM9数字签名算法验证过程示意图
今天的课程就到这里啦,下一堂课我们将学习数字签名算法在区块链中的应用,带大家继续了解数字签名,敬请期待!

-- 完 --
关注点宽学园,每周持续更新区块链系列课程,小宽带你进入区块链世界。我们下节课见啦。
【区块链与密码学】课堂回顾:
以上是关于区块链与密码学第6-7讲:SM9数字签名算法的主要内容,如果未能解决你的问题,请参考以下文章