自动驾驶中激光雷达如何检测障碍物

Posted 2022-03-21 泠山

自动驾驶中激光雷达如何检测障碍物

• 1. 介绍
• • 1.1 激光雷达-一种三维激光传感器
  • 1.2 激光雷达的优缺点？
  • 1.3 基于激光雷达如何进行障碍物检测？
  • 1.4 点云处理难点
• 2. 点云处理
• • 2.1 点云处理-体素网格
  • • 2.1.1 什么是体素网格？
• 3 三维点云的分割
• • 3.1 RANSAC
  • • 3.1.1 RANSAC 的实现
• 4. 障碍聚类
• • 4.1 点云聚类
  • • 4.1.1 计算 KD-Tree
    • 4.1.2 欧式聚类
  • 4.2 最邻近(NN)问题
  • • 4.2.1 为什么 NN 问题很重要
    • 4.2.2 为什么点云的 NN 很困难
    • 4.2.1 为什么最邻近在点云中如此困难
  • 4.3 BST(Binary Search Tree), kd-tree, octree 核心思想
  • 4.4 二叉树
  • • 4.4.1 BST 构建/插入
    • • 4.4.1.1 BST 插入复杂度
    • 4.4.2 BST 查找
    • 4.4.3 1NN 查找最邻近
    • 4.4.4 kNN 查找最邻近（N 个最邻近）
  • 4.5 Kd-tree
  • • 4.5.1 Kd-tree的构建
    • 4.5.2 Kd-tree的两种方式
• 5. 边界框
• 5.1 PCA
• • 5.1.1 PCA 应用
  • 5.1.2 Singular Value Decomposition (SVD)
  • 5.1.3 PCA 理论
  • • 5.1.4 PCA 应用一：降维
    • 5.1.5 Kernel PCA
    • 5.1.5 PCA 应用
• 6. 滤波
• • 6.1 Noise removal
  • • 6.1.1 Radius Outlier
    • 6.1.2 升级版：Statistical Outlier Removal
  • 6.2 Downsampling
  • • 6.2.1 Voxel Grid Downsampling

Reference:

1. 高翔，张涛 《视觉SLAM十四讲》
2. 自动驾驶中激光雷达检测障碍物理论与实践

激光雷达是利用激光束来感知三维世界，通过测量激光返回所需的时间输出为点云。它集成在自动驾驶、无人机、机器人、卫星、火箭等许多领域。

1. 介绍

1.1 激光雷达-一种三维激光传感器

激光雷达传感器利用光原理进行工作，激光雷达代表光探测和测距。它们可以探测到 300m 以内的障碍物，并准确估计它们的位置。在自动驾驶汽车中，这是用于位置估计的最精确的传感器。
激光雷达传感器由两部分组成：激光发射（顶部）和激光接收（底部）。发射系统的工作原理是利用多层激光束，层数越多，激光雷达就越精确。层数越多，传感器就越大。激光被发射到障碍物并反射，当这些激光击中障碍物时，它们会产生一组点云，传感器与飞行时间（TOF）进行工作，从本质上说，它测量的是每束激光反射回来所需的时间。如下图：
当激光雷达的质量和价格非常高时，激光雷达是可以创建丰富的三维环境，并且每秒最多可以发射200万个点。点云表示三维世界激光雷达传感器获得每个撞击点的精确 $(X,Y,Z)$位置。
激光雷达传感器可以是固态的，也可以是旋转的，固态激光雷达将把检测的重点放在一个位置上，并提供一个覆盖范围（比如FOV为90°）。在后一种情况下，它将围绕自身旋转，并提供360°旋转。在这种情况下，一般把它放在设备顶上，以提高能见度。

激光雷达很少用作独立传感器。它们通常与相机或雷达结合在一起，这一过程称为传感器融合。融合过程可分为早期融合和后期融合。早期融合是指点云与图像像素融合，后期融合是指单个检测物的融合。

1.2 激光雷达的优缺点？

缺点：

• 激光雷达不能直接估计速度。他们需要计算两个连续测量值之间的差值。
• 激光雷达在恶劣的天气条件下工作不好。在有雾或者下雨的情况下，激光会击中它，使场景变得混乱。
• 激光雷达的价格虽然在下降，但仍然很高。

优点：

• 激光雷达可以精确地估计障碍物的位置。到目前为止，还没有更准确的方法。
• 激光雷达处理点云。如果我们看到车辆前方的点云，即使障碍物检测系统没有检测到任何东西，我们也可以及时停车。这是一个很大的安全保证，车辆将不仅依赖于图像的神经网络和概率问题。

1.3 基于激光雷达如何进行障碍物检测？

激光雷达进行障碍物的步骤通常分为 4 个步骤：

1. 点云处理
2. 点云分割
3. 障碍聚类
4. 边界框拟合

1.4 点云处理难点

1. 稀疏的；

2. 不规则----搜索邻居比较困难；

3. 缺乏纹理信息；

4. 无序的----深度学习很困难；
   $$\left[\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ ⋮& ⋮& ⋮\\ x_N& y_N& z_N\end{array}\right]=\left[\begin{array}{ccc}{x}_2& y_2& z_2\\ x_1& y_1& z_1\\ ⋮& ⋮& ⋮\\ x_k& y_k& z_k\end{array}\right]$$

   如上面的行换了，表达的还是同一个物体。对于深度学习而言，输入进去的矩阵是不一样的就会产生不同的输出，但是我们希望输出是一样的。

5. 旋转同变性/不变性：我们旋转一些点，它的坐标是不一样的，但是它还是同一个物体。

2. 点云处理

2.1 点云处理-体素网格

为了处理点云，我们可以使用最流行的库 PCL(point cloud library)。它在 Python 中可用，但是在 C++ 中使用它更为合理，因为语言更适合机器人学。它也符合 ROS(机器人操作系统)。PCL 库可以完成探测障碍物所需的大部分计算，从加载点到执行算法。这个库相当于 OpenCV 的计算机视觉。因为激光雷达的输出很容易达到每秒 100000 个点，所以我们需要使用一种称为体素网格的方法来对点云进行下采样。

2.1.1 什么是体素网格？

体素网格 是一个三维立方体，通过每个立方体只留下一个点来过滤点云。立方体越大，点云的最终分辨率越低。最终，我们可以将点云的采样从几万点减少到几千点。
滤波完成后我们可以进行的第二个操作是 ROI(感兴趣区域) 的提取，我们只需删除不属于特定区域的每一些点云数据，例如左右距离 10m 以上的点云，前后超过 100m 的点云都通过滤波器滤除。现在我们有了降采样并滤波后的点云了，此时可以继续进行点云的分割、聚类和边界框实现。

3 三维点云的分割

3.1 RANSAC

点云分割任务是将场景与其中的障碍物分离开来，其实就是地面的分割。一种非常流行的分割方法称为 RANSAC(Random Sample consenses)。该算法的目标是识别一组点中的异常值。点云的输出通常表示一些形状。有些形状表示障碍物，有些只是表示地面上的反射。RANSAC 的目标是识别这些点，并通过拟合平面或直线(拟合的是地面)将它们与其他点分开。
为了拟合直线，我们可以考虑线性回归。但是有这么多的异常值，线性回归会试图平均结果，而得出错误的拟合结果，与线性回归相反，这里的 RANSAC 算法将识别这些异常值，且不会拟合它们。

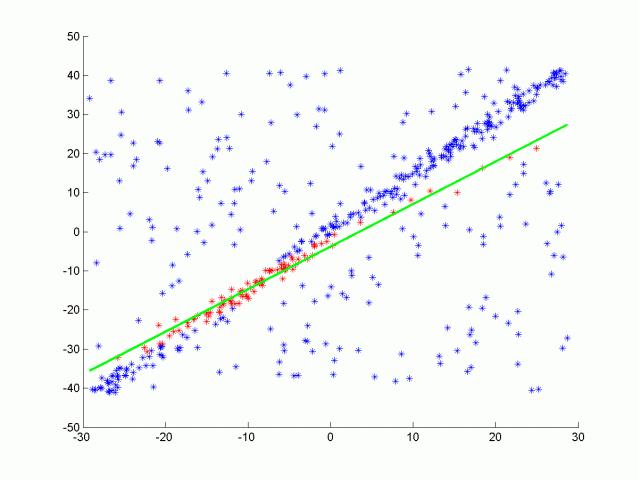
如上图所示我们可以将这条线视为场景的目标路径（即道路），而孤立点则是障碍物。

3.1.1 RANSAC 的实现

过程如下：

• 随机选取2个点
• 将线性模型拟合到这些点计算每隔一点到拟合线的距离。如果距离在定义的阈值距离公差范围内，则将该点添加到内联线列表中。

因此需要算法一个参数：距离阈值。

最后选择内点最多的迭代作为模型；其余的都是离群值。这样，我们就可以把每一个内点视为道路的一部分，把每一个外点视为障碍的一部分。RANSAC应用在3D点云中。在这种情况下，3个点之间的构成的平面是算法的基础。然后计算点到平面的距离。

下面点云为 RANSAC 算法的结果，紫色区域代表车辆（RANSAC 在这里应该只用来区分地面了）：

RANSAC 是一个非常强大和简单的点云分割算法。它试图找到属于同一形状的点云和不属于同一形状的点云，然后将其分开。

4. 障碍聚类

4.1 点云聚类

RANSAC 的输出是障碍点云和地面。由此，可以为每个障碍定义独立的簇。它是如何工作的？

聚类是一系列机器学习算法，包括：k-means（最流行）、DBScan、HDBScan 等。这里可以简单地使用欧几里德聚类，计算点之间的欧几里德距离。

4.1.1 计算 KD-Tree

在进行点云聚类问题时，由于一个激光雷达传感器可以输出几万个点云，这将意味有上万次的欧几里德距离计算。为了避免计算每个点的距离，这里使用 KD-Tree 进行加速。

KD-Tree 是一种搜索算法，它将根据点在树中的XY位置对点进行排序，一般的想法-如果一个点不在定义的距离阈值内，那么x或y更大的点肯定不会在这个距离内。这样，我们就不必计算每一个点云。

4.1.2 欧式聚类

过程如下：

• 选取两个点，一个目标点和一个当前点；
• 如果目标和当前点之间的距离在距离公差范围内，请将当前点添加到簇中。
• 如果没有，选择另一个当前点并重复。

点云欧式聚类算法就是将一组点云按其距离进行分割。聚类算法以距离阈值、最小聚类数目和最大聚类数目作为输入。通过这种方式，可以过滤“幽灵障碍物”（一个单点云在空间中是没有理由存在的），并定义一个封闭的障碍物距离。如下图这里用不同颜色来代表聚类后的障碍物点云簇。

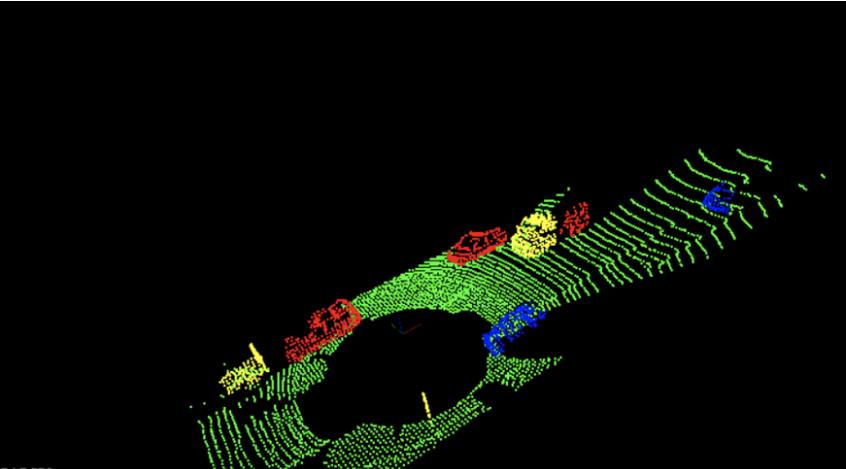
4.2 最邻近(NN)问题

• K-NN
  在空间 $M$ 中给定点集 $S$，一个查询点 $q\in M$，在 $S$ 中查找 $k$ 个最近点。
  

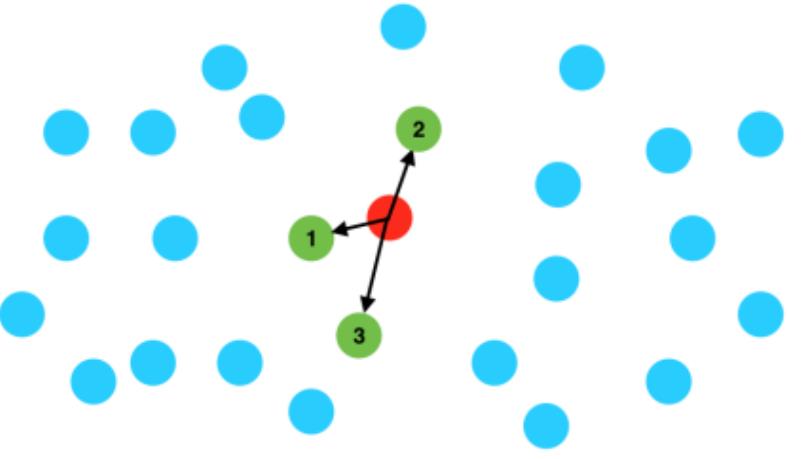
• Fixed Radius-NN
  在空间 $M$ 中给定点集 $S$，一个查询点 $q\in M$，在 $S$ 中查找所有符合 $||s-q||<r$ 的点。
  

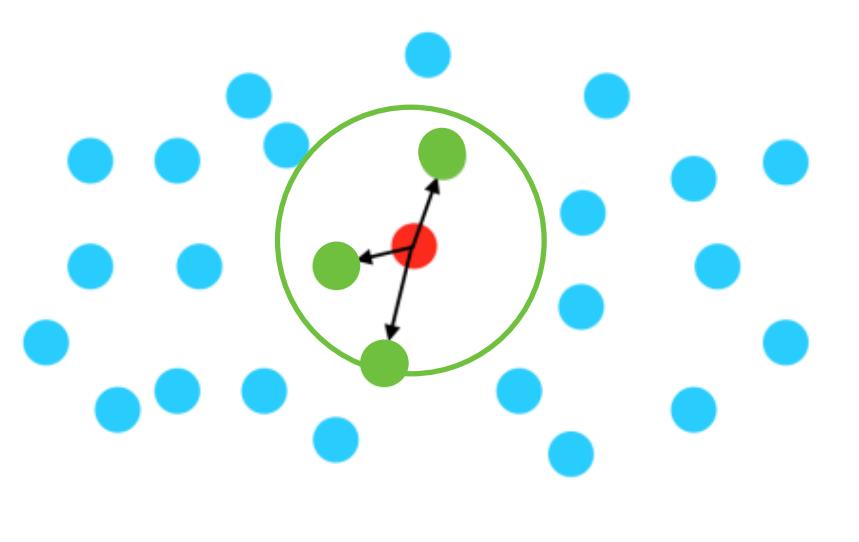
4.2.1 为什么 NN 问题很重要

1. 它几乎无处不在
   • 表面法向量估计
   • 噪声滤波
   • 采样
   • 聚类
   • 深度学习
   • 特征检测 / 描述
2. 为什么不简单的直接调用开源库（flann, PCL, ect.）
   • 它们不够高效：它们是通常使用的库，没有对 2D/3D 做优化；大多数开源的八叉树实现是低效的，而八叉树在 3D 中是最有效率的
   • 很少有 NN 库基于 GPU 的

4.2.2 为什么点云的 NN 很困难

1. 不规则：点云可以分布在任何地方
2. 维度灾难：点云可以是三维的，与二维相比的数据量是指数上升的。也可以建立一个三维网格，将点云转化成图像一样的东西，但是网格大部分区域是空白的，而且网格大小的选取也是一个问题。因此使用网格并不高效。

4.2.1 为什么最邻近在点云中如此困难

图像：
一个邻居简单的表示为 $x+\Delta x,y+\Delta y$.
点云：

• 不规则的：可以分布在图像中任何一个地方；
• 维数灾难：网格大部分是空白的，原理上就很低效。

4.3 BST(Binary Search Tree), kd-tree, octree 核心思想

• 空间分割：
  1. 将空间划分成不同面积；
  2. 只寻找一部分区域，而不是所有的数据点。
• 停止标准：
  1. 如何跳过一些区域：每个区域都会有一个最差距离；
  2. 如何停止 k-NN/radius-NN 查找: 如果知道可能的结果都在某个区间里面，那么查找完就结束了；

4.4 二叉树

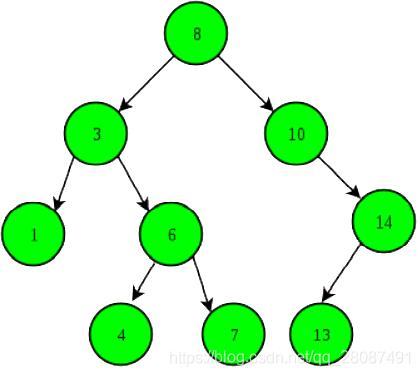
BST 是一个基于节点的树结构：

1. 左边的 key 都要比中间 root 小，右边的大。

一个节点包含：

• Key；
• Left child;
• Right child;
• … …

4.4.1 BST 构建/插入

比较小放左边，比较大放右边。如果左右边被占据了，就跟左右边被占据的继续对比。
给定一个一维点集 $x_1,x_2,...,x_n,x_i\in \mathbb{R}$，如一个数组：$[100,20,500,10,30,40]$

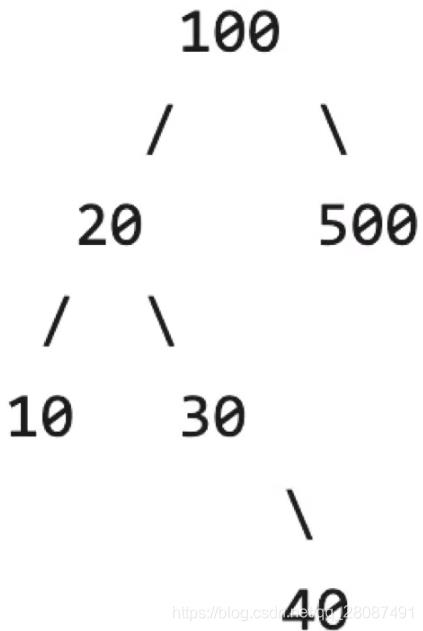
4.4.1.1 BST 插入复杂度

最坏的情况是 $O(h)$，在这里 $h$ 为在 BST 中点的个数。如将数组 [9,8,7,6,5,4,3] 按顺序插入进一个空的 BST 中：

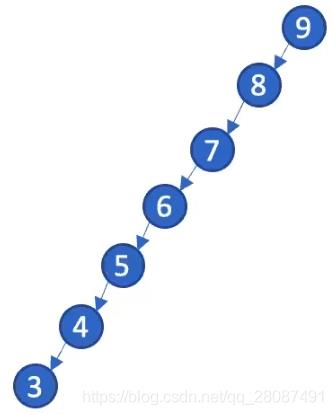
这是一个合法的二叉树但它一无是处。平衡二叉树是另一个话题了。最佳情况：$h=lo{g}_{2}n$。

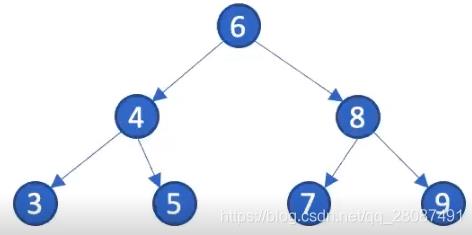
4.4.2 BST 查找

给定一个 BST 和一个待查找 key，决定哪一个 node 等于这个 key，如果没有，则返回 NULL。

4.4.3 1NN 查找最邻近

比如说在下图中查找点 11：
汽车激光雷达有啥用

自动驾驶感知算法实战2——激光雷达原理介绍

自动驾驶感知算法实战2——激光雷达原理介绍

如何通过16线激光雷达实现无人车的避障

在行驶中前方有障碍物，无人驾驶技术可以自动识别吗？

汽车激光雷达有啥用？激光雷达和毫米波雷达的区别