数字信号处理线性时不变系统 LTI ( 判断某个系统是否是 “ 线性 “ 系统 | 案例四 )

Posted 2022-02-26 韩曙亮

文章目录

• 一、判断某个系统是否是 “ 线性 “ 系统

一、判断某个系统是否是 “ 线性 “ 系统

---

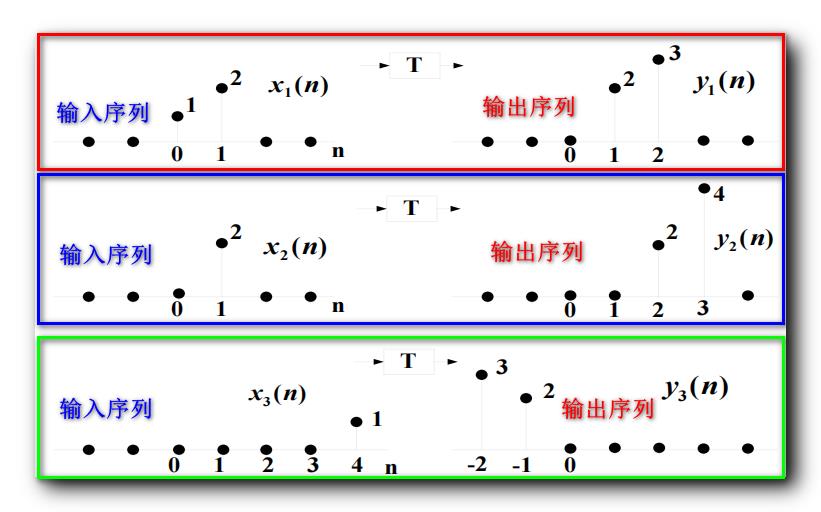
系统 $T$ 是 " 时不变系统 " , 输入序列 与 输出序列 如下图所示 :

输入为 $x_1(n)$ 序列时 , 输出是 $y_1(n)$ 序列 ;

输入为 $x_2(n)$ 序列时 , 输出是 $y_2(n)$ 序列 ;

输入为 $x_3(n)$ 序列时 , 输出是 $y_3(n)$ 序列 ;

判断上图中的系统 $T$ 是是否是 线性系统 ;

当系统为 $T[\delta (n)]$ 时 , 输出是什么 ;

$x_1(n)=\delta (n)+2\delta (n-1)$ , $y_1(n)=2\delta (n-1)+3\delta (n-2)$

$x_2(n)=2\delta (n-1)$ , $y_2(n)=2\delta (n-2)+4\delta (n-3)$

$x_3(n)=\delta (n-4)$ , $y_3(n)=2\delta (n+1)+3\delta (n+2)$

$x_1(n)=x_2(n)+x_3(n+4)$ , 令 $x_1(n)$ 中的 $\delta (n)$ 等于 $x_3(n)$ 中的 $\delta (n-4)$ , 向左移 $4$ 即可 ;

在该系统是 " 时不变 " 系统的前提下 , 如果 $y_1(n)=y_2(n)+y_3(n+4)$ , 那么说明该系统是 " 线性 " 系统 ;

$y_1(n)=y_2(n)+y_3(n+4)$

$y_2(n)+y_3(n+4)=2\delta (n-2)+4\delta (n-3)+2\delta (n+5)+3\delta (n+6)$ , 明显不等于 $y_1(n)=2\delta (n-1)+3\delta (n-2)$ ;

该系统 , 不是 " 线性 " 系统 ;

$T[\delta (n)]$ 系统中 , 如果 输入是 $\delta (n)$ 序列 , 则对应的 " 变换 " 后的输出是 $y_3(n+4)=2\delta (n+5)+3\delta (n+6)$ , 得到如下公式 :
$$T[\delta (n)]=2\delta (n+5)+3\delta (n+6)$$