N位加减法运算器实现(Verilog HDL)|计算机组成
Posted 桃陉
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了N位加减法运算器实现(Verilog HDL)|计算机组成相关的知识,希望对你有一定的参考价值。
前言:
简单的加法器我们都认识,即一个加数一个被加数,相加后得到和;今天我们要首先介绍的是全加器,它除了加数与被加数外,还存在低位进位,得到的结果除了和还有高位进位。之后会介绍与之类似的减法器;最后将二者综合起来得到双符号位(判断是否溢出)的补码加减法计算器。
1.一位全加器的设计
∙
\\bullet
∙ 对于一位全加器,它的加数、被加数、和都是一位的二进制数,它的低位进位和高位进位也是一位的二进制数,其中1表示需要进位,0表示不需要进位。
∙
\\bullet
∙ 我们可以简单的列一个运算表格如下(前三列为输入项,后两列为输出项):
| Ai | Bi | Ci | Si | Ci+1 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
其中Ai为加数、Bi为被加数,Ci为低位进位,Si为和,Ci+1为高位进位。我们可以发现当输入数据中出现奇数个1时和就为1,偶数个1时和为0,所以我们可以采用异或^的逻辑操作进行运算。
a
s
s
i
g
n
s
=
a
∧
b
∧
c
i
assign \\ s=a \\wedge b \\wedge ci
assign s=a∧b∧ci
而对于高位进位操作,我们只要判断是否有大于等于两个1,如果满足就会发生进位那么高位进位为1,反之为0。
a
s
s
i
g
n
c
o
=
a
&
c
i
∣
b
&
c
i
∣
a
&
b
assign \\ co=a\\&ci\\ | \\ b\\&ci\\ | \\ a\\&b
assign co=a&ci ∣ b&ci ∣ a&b
但是我们可以直接用拼接的方法,将和与高位进位分离出来,下面上代码:
module add_1bit(
input a,b,cin,
output s,cout
);
assign cout,s=a+b+cin;
endmodule
因为是1位全加器,所以最多产生两位的结果,我们将高1位赋为cout,低1位赋为s。
我们进行仿真,将上面八种情况一一输出:
module add_1bit_sim();
reg a,b,cin;
wire s,cout;
add_1bit uut(.a(a),
.b(b),
.cin(cin),
.s(s),
.cout(cout));
initial begin
a=0;b=0;cin=0;
begin a=0;b=0;cin=0;#100;end
begin a=0;b=0;cin=1;#100;end
begin a=0;b=1;cin=0;#100;end
begin a=0;b=1;cin=1;#100;end
begin a=1;b=0;cin=0;#100;end
begin a=1;b=0;cin=1;#100;end
begin a=1;b=1;cin=0;#100;end
begin a=1;b=1;cin=1;#100;end
end
endmodule
仿真结果波形所下:
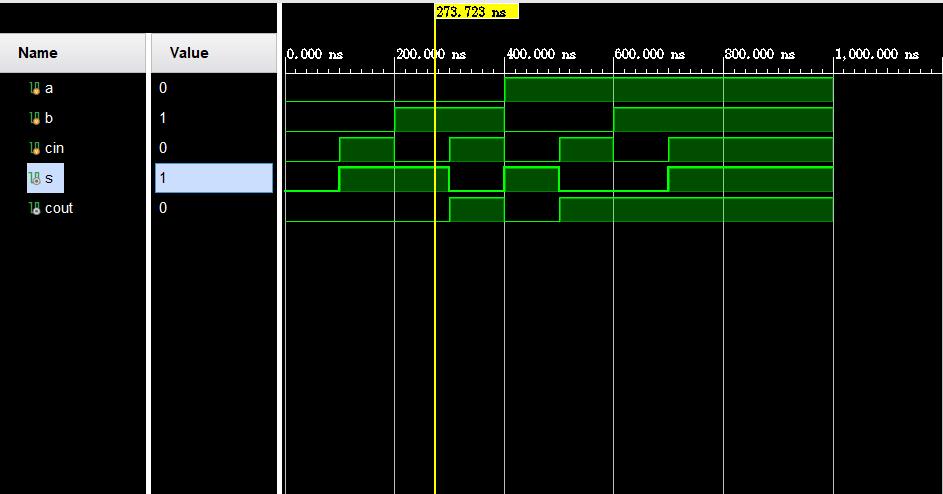
2.N位全加器的设计(无符号)
对于N位全加器,我们只是在1位全加器基础之上的拓展。我们将加数a、被加数b、和s的长度都扩展为N位,进位标识仍然为1位。
同样采用拼接的方法,分离cout、s:
module add_Nbit(a,b,cin,s,cout);
parameter N=8;
input [N-1:0]a,b;
input cin;
output [N-1:0]s;
output cout;
assign cout,s=a+b+cin;
endmodule
仿真代码如下:
module add_Nbit_sim();
reg [7:0]a=8'b00000000;
reg [7:0]b=8'b00000000;
reg cin=0;
wire [7:0]s;
wire cout;
add_Nbit uut(.a(a),
.b(b),
.cin(cin),
.s(s),
.cout(cout));
initial begin
#100 a=8'b00000000;b=8'b10100000;
#100 a=8'b11111110;b=8'b11111110;
#100 a=8'b11111111;b=8'b01111111;
end
endmodule
仿真结果波形如下:
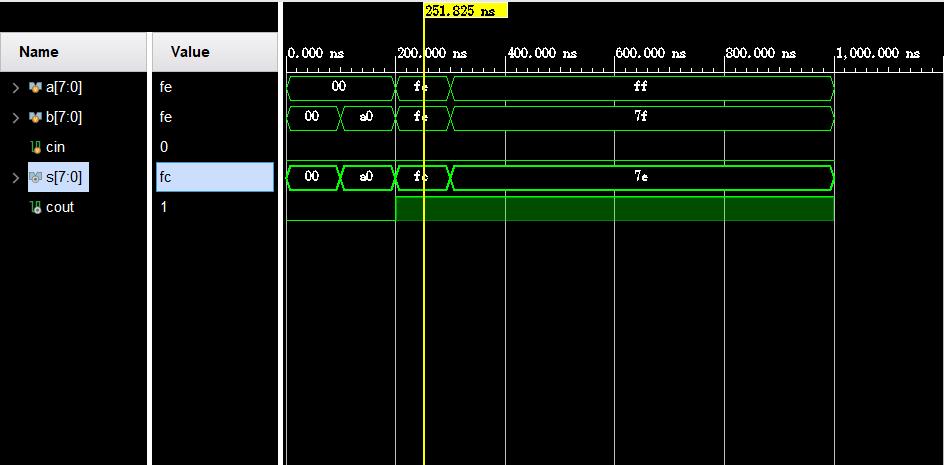
3.N位减法器的设计(无符号)
N位减法器的设计与N位加法器设计基本相同,我们设置一位二进制数a为被减数,减去b和低位的借位cin,输出相减的结果s和向相邻高位的借位cout;
同样采用拼接的方法,分离cout、s:
module sub_Nbit(a,b,cin,s,cout);
parameter N=8;
input [N-1:0]a,b;
input cin;
output [N-1:0]s;
output cout;
assign cout,s=a-b-cin;
endmodule
仿真代码如下:
module sub_Nbit_sim();
reg [7:0]a=8'b11111111;
reg [7:0]b=8'b11111111;
reg cin=0;
wire [7:0]s;
wire cout;
sub_Nbit uut(.a(a),
.b(b),
.cin(cin),
.s(s),
.cout(cout));
initial begin
#100 a=8'b00000000;b=8'b10100000;
#100 a=8'b11111111;b=8'b11111110;
#100 a=8'b11111111;b=8'b01111111;
end
endmodule
仿真结果波形如下:
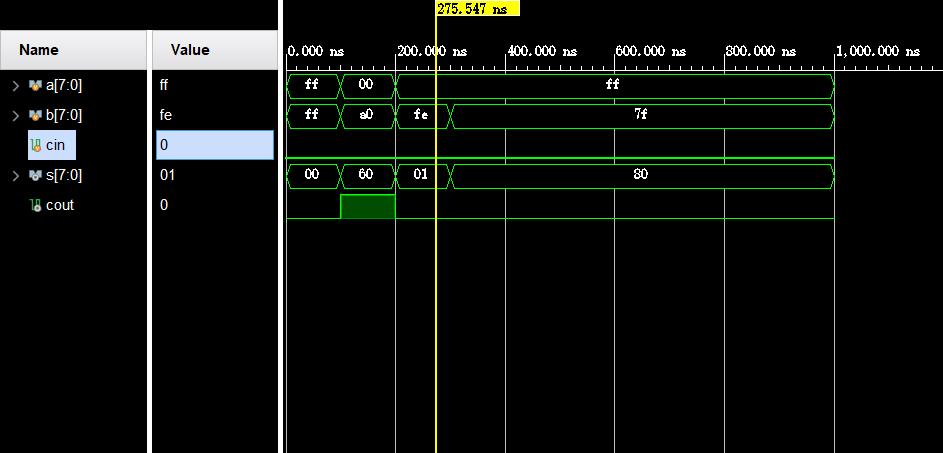
4.N位补码加减法运算器
最后我们设计一个补码的加减法计算器,其中a、b、s均为补码,我们设置一位control用来控制需要进行的操作,其中0为加法,1为减法。
| 变量 | 长度 | 输入/输出 | 含义 |
|---|---|---|---|
| a | N | input | 第一个操作数 |
| b | N | input | 第二个操作数 |
| control | 1 | input | 控制加减法操作 |
| cout | 1 | output | 进位标识 |
| overflow | 1 | output | 溢出标识 |
| s | N | output | 输出结果 |
代码如下:因为采用双符号的做法,所以我们将操作数按符号拓展一位,即现在高两位为符号。两位相异即为溢出。
module add_sub(a,b,control,cout,overflow,s);
parameter N=4;
input [N-1:0]a,b;
input control;
output reg cout,overflow;
output reg [N-1:0]s;
reg [N:0]a2,b2,s2;
always@(*) begin
//符号拓展一位
a2[N]=a[N-1];
a2[N-1:0]=a[N-1:0];
b2[N]=b[N-1];
b2[N-1:0]=b[N-1:0];
//判断运算类型
if(control==0) cout,s2=a2+b2;
else cout,s2=a2+(~b2)+control;
//判断是否溢出
if((s2[N]^s2[N-1])==1) overflow=1;
else overflow=0;
//取出结果
s[N-1:0]=s2[N-1:0];
end
endmodule
仿真代码如下:
module add_sub_sim();
reg [3:0]a=4'b0000;
reg [3:0]b=4'b0000;
reg control=0;
wire [3:0]s;
wire cout,overflow;
add_sub as(.a(a),
.b(b),
.control(control),
.s(s),
.cout(cout),
.overflow(overflow));
initial begin
begin #100 a=4'b1001;b=4'b1000;end
begin #100 a=4'b0010;b=4'b0000;end
begin #100 a=4'b0011;b=4'b1000;end
begin #100 a=4'b1111;b=4'b1111;end
begin #100 a=4'b0001;b=4'b1000;end
control=1;
begin #100 a=4'b0010;b=4'b0000;end
begin #100 a=4'b0011;b=4'b1000;end
begin #100 a=4'b0000;b=4'b1111;end
end
endmodule
仿真结果波形如下:
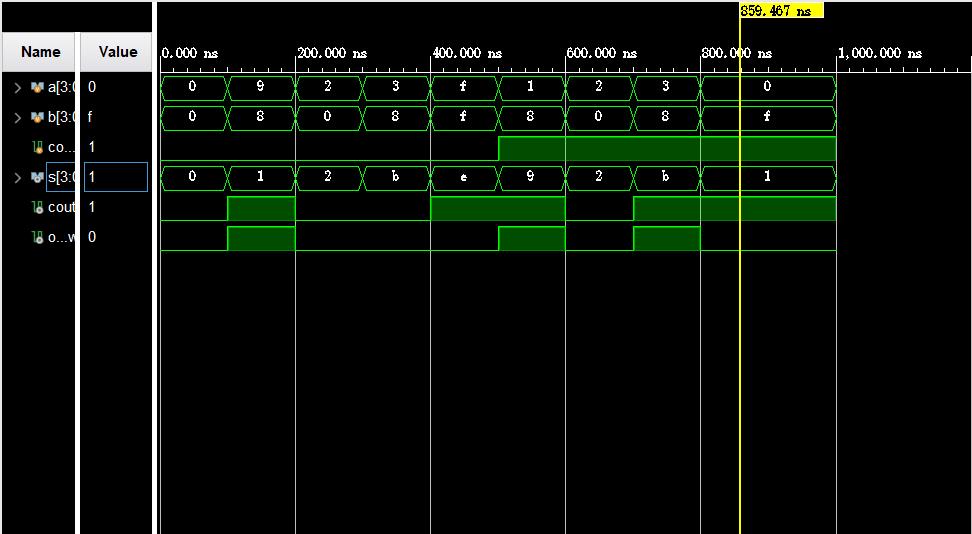
以上是关于N位加减法运算器实现(Verilog HDL)|计算机组成的主要内容,如果未能解决你的问题,请参考以下文章
xilinx /FPGA/ verilog HDL不同位数的数相加,如何进行?
使用74LS83构成4位二进制全加\全减器。 具体要求:1)列出真值表; 2)画出逻辑图; 3)用Verilog HDL仿真