感知机算法
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了感知机算法相关的知识,希望对你有一定的参考价值。
参考技术A 本文主要参考文章 https://www.sohu.com/a/148318381_717210感知机算法主要用来处理二分类问题,并且是线性可分的二分类问题。
感知机算法思想:构造一个超平面,这个超平面可以把空间分为两类,一类的数据是正类,另一类的数据是负类。那么什么是超平面呢。超平面分离定理是应用凸集到最优化理论中的重要结果,这个结果在最优化理论中有重要的位置。所谓两个凸集分离,直观地看是指两个凸集合没有交叉和重合的部分,因此可以用一张超平面将两者隔在两边。
感知机的公式为:f(x) = sign(wx + b) 我们的目的就是要求 w 和 b ,怎样可以完美的划分两类数据。其中w,b为模型参数,w为权值,b为偏置。wx表示w,x的内积。这里sign是激励函数:
我们通过不断的优化这个超平面, wx+b,是的误分类的数据越来越小。主要利用的思想是梯度下降和误分类点到超平面的一个距离。
距离公式如下:
如何判断误分类点呢。误分类点肯定满足如下公式:-yi(wx+b)>0 因为误分类点到超平面距离一定是大于0的,因此我们可以将绝对值去掉。得到损失函数如下:
使用梯度下降法来进行更新:
感知机学习算法(PLA)
Perception Learning Algorithm, PLA
1.感知机
感知机是一种线性分类模型,属于判别模型。
感知机模型给出了由输入空间到输出空间的映射:
f(X) = sign(WTX + b)
简单来说,就是找到一个分类超平面 WTX + b =0,将数据集中的正例和反例完全分开。
2.感知机学习算法(PLA)
感知机学习算法是为了找到 W 和 b 以确定分类超平面。为了减少符号,令 W = [b, W1, W2, ..., Wn], X = [1, X1, X2, ..., Xn],则 f(X) = sign(WTX )。
感知机学习算法是由误分类驱动的:
- 对于实际为正例(y=1)的误分类点,则对 W 进行如下修正:
W = W + X
从而使得 WTX 变大,更接近大于 0, 即更接近正确分类; (W+X)TX = WTX + ||X||2
- 对于实际为正例(y=1)的误分类点,则对 W 进行如下修正:
W = W - X
从而使得 WTX 变小,更接近小于 0, 即更接近正确分类; (W-X)TX = WTX - ||X||2
综上,令 W 初值 W0=0,然后每次选取一个误分类点,更新 W = W + y X ,直到所有点都被正确分类。
PS:不同的初值或者选取不同的误分类点,解可以不同。
具体算法如下:

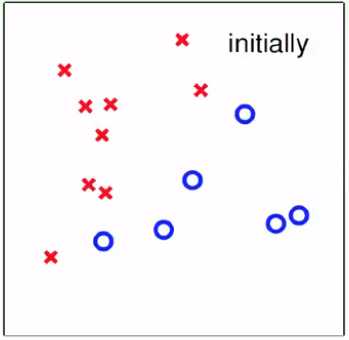
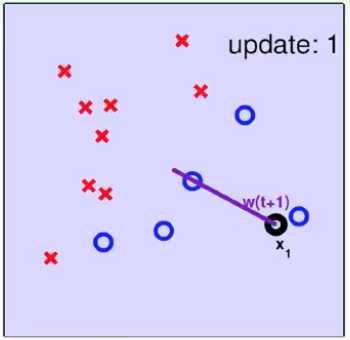
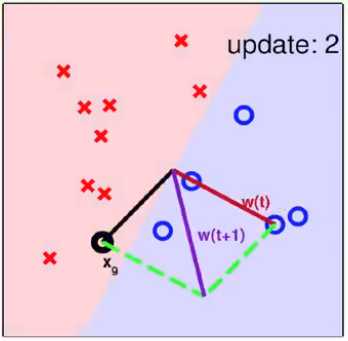
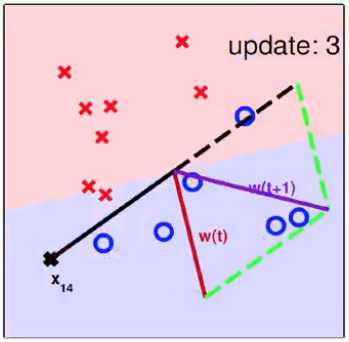
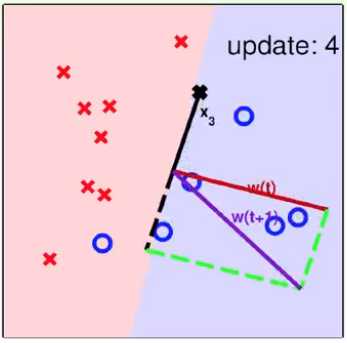
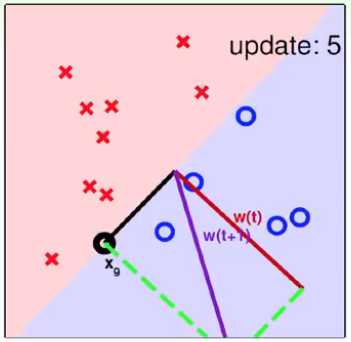
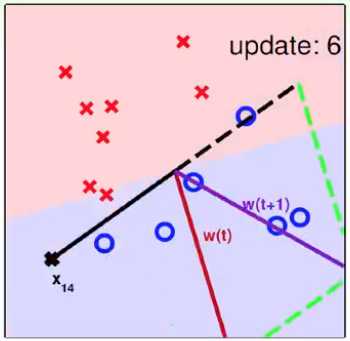
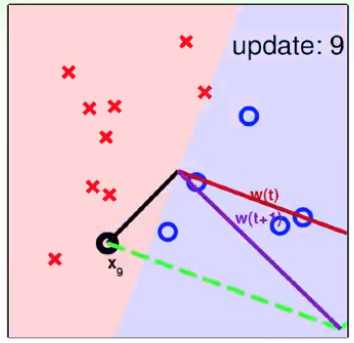
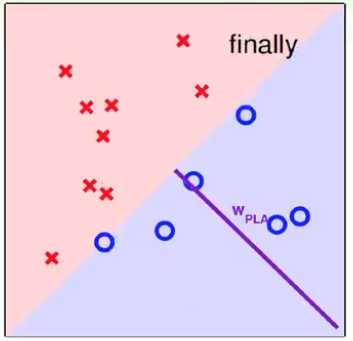
3. PLA算法的收敛性
首先,确定数据集是 线性可分 的,否则,PLA永远不收敛。
假设数据集线性可分,则一定存在一个分类超平面可以将正例负例完全区分。
设最优的参数为 Wf,则:
yi WfTXi ≥ minn(ynWfTXn) > 0
已知 WfTW 越大,则 W 与 Wf 越接近。(联想协方差)
WfTWT = WfT (WT-1+ yT-1 XT-1 )
= WfT WT-1 + yT-1WfTXT-1
≥ WfT WT-1 + minn(ynWfTXn) (1)
> WfT WT-1 + 0
然而,WfTW 越大,也有可能只是 W 的元素值放大,但是W 与 Wf 的角度却没有接近。
所以,我们要讨论 $frac{W_{f}^{T}W_{T}}{left | W_{f} ight |left | W_{T} ight |}$ 是否越来越大,若是,则 W 越来越接近最优值 Wf 。(联想 SVM 中 函数间隔 和 集合间隔 的概念)
我们知道,PLA 是误分类点驱动,所以有:
yi WTXi ≤ 0
又有:
WT = WT-1 + yT-1 XT-1
则:
|| WT ||2 = || WT-1 ||2 + yT-12 || XT-1 ||2 + 2 yT-1 WT-1T XT-1
≤ || WT-1 ||2 + yT-12 || XT-1 ||2 = || WT-1 ||2 + || XT-1 ||2
≤ || WT-1 ||2 + minn|| Xn ||2 (2)
设 W0 = 0
令 ρ = minn(ynWfTXn) ,代入式 (1):
WfTWT ≥ WfT WT-1 + ρ ≥ WfT WT-2 + 2ρ ≥ ... ≥ WfT W0 + Tρ = T