数据结构树 学习笔记随笔

Posted 2022-12-04 Hot Autumn

二叉树的第 i 层上最多有 2^i-1 个结点。

深度为 k 的二叉树最多有 2^k-1 个结点。

对于一颗二叉树，叶子结点（度为0）n₀ 个，度为 2 的结点数为 n₂，则 n₀ = n₂ + 1。

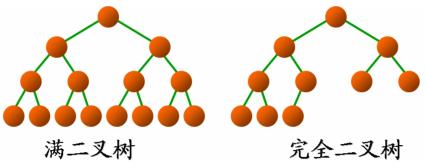
满二叉树：深度为 k 且有 2^k-1 个结点。

完全二叉树：深度为 k 有 n 个结点，当且仅当每个结点都与深度为 k 的满二叉树中编号从 1 到 n 的结点一一对应。

具有 n 个结点的完全二叉树的深度为「log₂n」+ 1。其中用「」表示向下取整。

二叉树转换为森林

1、若节点 x 是双亲 y 的左孩子，则把 x、以及 x 的右孩子，右孩子的右孩子，...，都与 y 用线连起来。

2、去掉所有双亲到右孩子的连线。

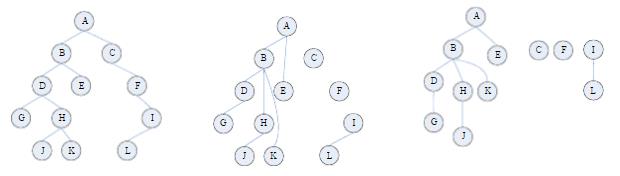
树转换为二叉树

树中每个节点最多只有一个最左边的孩子（长子）和一个右邻的兄弟

1、 在所有兄弟节点之间加一连线

2、 对每个节点，除了保留与其长子之间的连线外，去掉该节点与其他孩子的连线

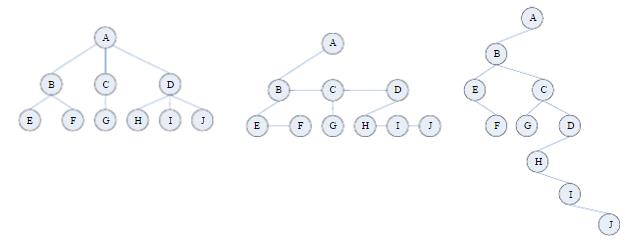
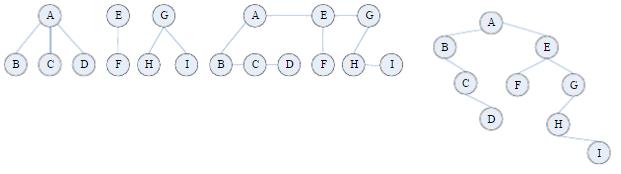
森林转换为二叉树

1、 将森林中的每棵树变为二叉树

2、 将各二叉树的根节点视为兄弟从左到右连接在一起，形成二叉树。

 

哈夫曼树必须是近的权值大，远的权值小。

 

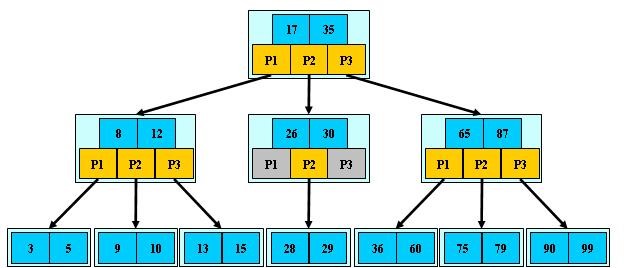
B- 树

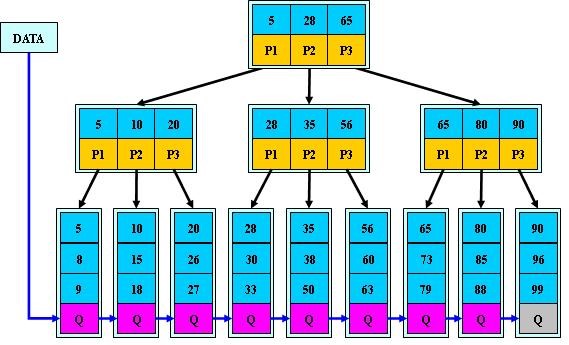
B+ 树

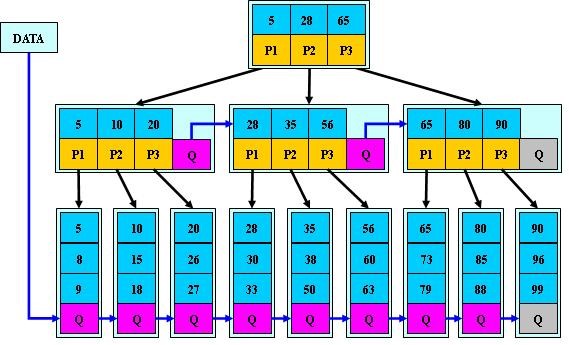
B* 树

它们所有叶子结点位于同一层。

B- 树：多路搜索树，一棵M阶的B- 树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点；所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

1. 树中每个结点至多有M棵子树；
2. 若根不是叶子结点，则至少有2棵子树；

3.除根之外，所有非叶子结点至少有「M/2」棵子树。

B+ 树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

与B- 树的差异在于：

1. 有n棵子树的结点中含有n个关键字；
2. 所有叶子结点中包含全部关键字信息，及指向这些关键字记录的指针，且叶子结点本身依赖关键字的大小自小而大顺序链接；

3.所有非叶子结点可以看成是索引部分，结点中仅含有其子树中最大（或最小）关键字

B* 树：在 B+ 树基础上，为非叶子结点也增加链表指针，将结点的最低利用率从 1/2 提高到 2/3。

为什么说B+树比B-树更适合实际应用中操作系统的文件索引和数据库索引？

1. 所谓索引，即是快速定位与查找，那么索引的结构组织要尽量减少查找过程中磁盘 I/O 的存取次数( B+ 树相比 B- 树，其非叶子节点占用更小的空间，可以有更多非叶子节点存放在再内存中，减少大量的 IO，非叶子节点相当于叶子节点的索引，所以可以将更多的索引存储到内存中)

2. 由于非终结点并不是最终指向文件内容的结点，而只是叶子结点中关键字的索引。所以任何关键字的查找必须走一条从根结点到叶子结点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。

红黑树和 AVL 树

一棵 AVL 树满足以下的条件：

1.  它的左子树和右子树都是 AVL 树；

2. 左子树和右子树的高度差不能超过 1；

从条件1可能看出是个递归定义，如 GNU 一样。是高度平衡的二次树
性质：

1.  一棵 n 个结点的 AVL 树的其高度保持在log n，不会超过3/2log(n+1)；
2.  一棵 n 个结点的 AVL 树的平均搜索长度和最坏情况都是保持在O(logn)；

3. 一棵 n 个结点的 AVL 树删除一个结点做平衡化旋转所需要的时间为O(log n)。

从第1点来看红黑树是牺牲了严格的高度平衡的优越条件为代价，红黑树能够以O(log n)的时间复杂度进行搜索、插入、删除操作。此外，由于它的设计，任何不平衡都会在三次旋转之内解决。当然，还有一些更好的，但实现起来更复杂的数据结构能够做到一步旋转之内达到平衡，但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和 AVL 相同，但统计性能比 AVL 树更高。