二叉树学习笔记

Posted 2021-04-09 爱搭建

二叉树的定义

        在计算机科学中，二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。一棵深度为k，且有2^k-1个节点的二叉树，称为满二叉树。

                                                                ——来源：百度百科

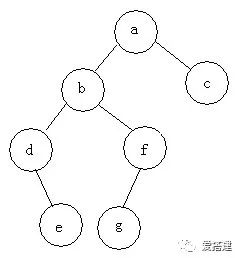
（图1）

咳咳咳......

说人话：

        二叉树就是类似于一个树的东西，就像这样：

      准确说应该倒过来：

    二叉树的根节点就是这棵树的树根（上图最顶端），二叉树的子节点就是树干上的树枝，每一个节点都有它的根节点，除了整棵树的根节点（如图1，a是整棵树的根节点，但相对d来说，b是d的根结点）在二叉树中，每个根节点最多只有两个子节点（每个树枝（树根）最多只能有两个比它本身小的树枝）。每个根结点左边所有节点连成的部分点叫做左子树，右边则相反。

二叉树的遍历

• 前序遍历顺序：根结点->左子树->右子树

  （先读根，然后读左边的树枝，再读右边的树枝）

• 中序遍历顺序：左子树->根结点->右子树

  （先读左边的树枝，然后读根，再读右边的树枝）
  

• 后序遍历顺序：左子树->右子树->根结点

  （先读左边的树枝，然后读右边的树枝，再读根）

  
  

  图1的遍历结果：

  前序遍历：abdefgc
  中序遍历：debgfac
  后序遍历：edgfbca
  

  
  

题目如下：

建立二叉树，然后实现（前序、中序、后序）遍历。

 输入格式：

第一行：结点个数n。n<=100; 以下n行，每行4个数依次是：结点编号，左子树编号，右子树编号。

输出格式：

输出遍历结果。

---

实现将一棵树前序遍历：

#include<bits/stdc++.h>。//万能头文件using namespace std;//做一个结构体struct aaa{      int date; //编号     int left;  //左子树    int right; //右子树}a[1001];//一个递归来遍历void dg(int k){     cout<<a[k].date<<" ";  //访问根节点    if (a[k].left!=0){             dg(a[k].left);   //查找左子树      }      if (a[k].right!=0){                dg(a[k].right);    //查找右子树    }    }//查找根节点函数int find(int n){     int b[1001]={0},cnt;        for (int i=1;i<=n;i++){                b[a[i].left]=1;        //这两个节点不可能是树根        b[a[i].right]=1;        }        for (int i=1;i<=n;i++){                if (b[i]==0){           //找树根          cnt=i;                }     }        return cnt;      //返回出去}int main(){     int n;     cin>>n;        int k;    for (int i=1;i<=n;i++){    cin>>k;     cin>>a[k].date>>a[k].left>>a[k].right;         }         k=find(n);    //查找到树根     dg(k);        //疯狂从树根开始递归！     return 0;     //华华丽丽的结束}

---

实现将一棵树中序遍历:

#include<bits/stdc++.h>。//万能头文件using namespace std;//做一个结构体来存二叉树struct aaa{  int date; //编号  int left; //左子树  int right; //右子树}a[1001];//一个递归来遍历void dg(int k){  if (a[k].left!=0){        dg(a[k].left);  //查找左子树   }  cout<<a[k].date<<" "; //访问根节点 if (a[k].right!=0){  dg(a[k].right); //查找右子树 } }//查找根节点函数int find(int n){  int b[1001]={0},cnt;  for (int i=1;i<=n;i++){  b[a[i].left]=1; //这两个节点不可能是树根 b[a[i].right]=1;  }  for (int i=1;i<=n;i++){  if (b[i]==0){ //找树根  cnt=i;  }  }  return cnt; //返回出去}int main(){  int n;  cin>>n;  int k; for (int i=1;i<=n;i++){ cin>>k; cin>>a[k].date>>a[k].left>>a[k].right;  }  k=find(n); //查找到树根 dg(k); //疯狂从树根开始递归！ return 0; //华华丽丽的结束}

---

实现将一棵树后续遍历：

#include<bits/stdc++.h>。//万能头文件using namespace std;//做一个结构体来存二叉树struct aaa{  int date; //编号  int left; //左子树  int right; //右子树}a[1001];//一个递归来遍历void dg(int k){  if (a[k].left!=0){     dg(a[k].left);  //查找左子树   }   if (a[k].right!=0){  dg(a[k].right); //查找右子树 }  cout<<a[k].date<<" "; //访问根节点}//查找根节点函数int find(int n){  int b[1001]={0},cnt;  for (int i=1;i<=n;i++){  b[a[i].left]=1; //这两个节点不可能是树根 b[a[i].right]=1;  }  for (int i=1;i<=n;i++){  if (b[i]==0){ //找树根  cnt=i;  }  }  return cnt; //返回出去}int main(){  int n;  cin>>n;  int k; for (int i=1;i<=n;i++){ cin>>k; cin>>a[k].date>>a[k].left>>a[k].right;  }  k=find(n); //查找到树根 dg(k); //疯狂从树根开始递归！ return 0; //华华丽丽的结束}

尾声

这次讲了二叉树的定义与遍历，如果讲的不好，请多多指教。大佬勿喷

（图片均来自网络）

扫描二维码

关注更多精彩