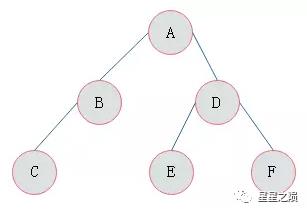
二二叉树

Posted 2021-05-05 星星之陨

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了二二叉树相关的知识，希望对你有一定的参考价值。

2.1、基本定义

二叉树是 n(n>=0)个节点的有限集合，该集合或者为空集（称为空二叉树），或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树组成。

特点：

每个节点最多有两棵子树，所以二叉树中不存在度大于 2 的节点。

左子树和右子树是有顺序的，次序不能任意颠倒。即使树中某节点只有一棵子树，也要区分它是左子树还是右子树。

五种基本形态：

空二叉树

只有一个根节点

根节点只有左子树

根节点只有右子树

根节点既有左子树又有右子树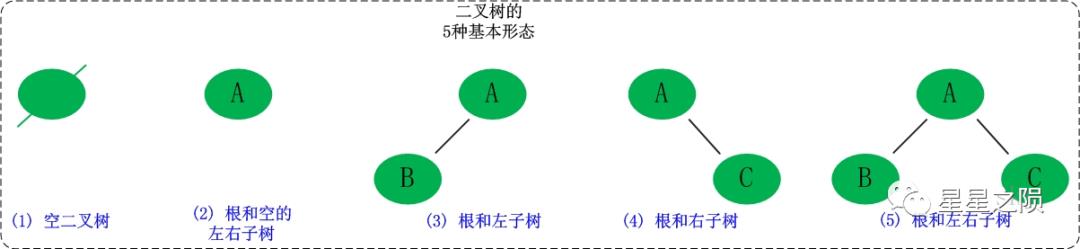

2.2、二叉树类型

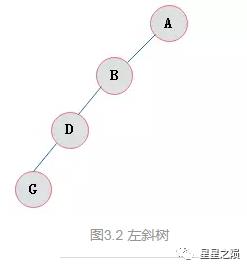
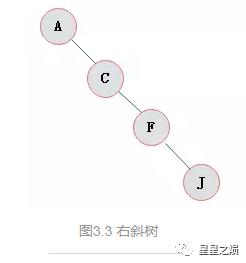
2.2.1、斜树

所有的节点都只有左子树的二叉树叫左斜树。所有节点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。

二、二叉树

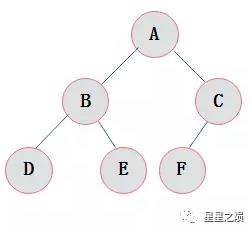
2.2.2、满二叉树

在一棵二叉树中。如果所有分支节点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

满二叉树的特点

叶子只能出现在最下一层。

非叶子节点的度一定是 2。

在同样深度的二叉树中，满二叉树的节点个数最多，叶子数最多。

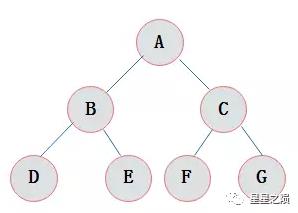
2.2.3、完全二叉树

对一棵具有n个节点的二叉树按层序编号，如果编号为i(1<=i<=n)的节点与同样深度的满二叉树中编号为i的节点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。

完全二叉树特点：

叶子节点只能出现在最下两层，且最下层的叶子节点都集中在二叉树左侧连续位置，倒数第二层若存在叶子节点，一定在右部连续位置。

如果有度为 1 的节点，只可能有 1 个，且该节点只有左子树。

同样节点数目的二叉树，完全二叉树深度最小。

满二叉树一定是完全二叉树，但反过来不一定成立。

完全二叉树与满二叉树：

二、二叉树

2.3、二叉树性质

性质 1

二叉树第层上的节点数目最多为

性质 2

深度为的二叉树至多有 ,个节点，最少有个节点。

性质 3

在一个二叉树中，如果叶子节点的个数为，度为 2 的节点个数为，则

性质 4

具有个节点的完全二叉树的深度为

性质 5

对一棵具有个节点的完全二叉树中的节点从 1 开始按层序编号，则对于任意的编号的节点，有：

(1) 如果 ,则节点的双亲编号为 ;否则节点是根节点。

(2) 如果，则节点的左孩子编号为；否则节点无左孩子。

(3) 如果，则节点的右孩子编号为；否则节点无右孩子。

2.4、二叉树的遍历

2.4.1、前序遍历

基本思想

访问根节点

前序遍历左子树

前序遍历右子树

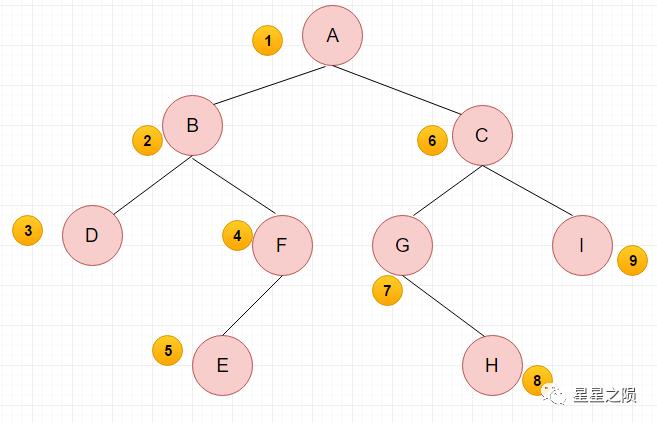
遍历结果：ABDFECGHI

顺序结果

首先访问根节点 A，然后遍历左子树 B A

访问 B，B 作为根节点，遍历其左子树 D AB

访问 D，D 作为根节点，左右子树为空，则遍历 B 的右子树 F ABD

访问 F，F 作为根节点，遍历其左子树 E ABDF

访问 E，E 作为根节点，左右子树为空，向上遍历 A 的右子树 C ABDFE

访问 C，C 作为根节点，遍历其左子树 G ABDFEC

访问 G，G 作为根节点，遍历其左子树，左子树为空，遍历其右子树 H ABDFECG

访问 H，H 作为根节点，左右子树为空，则遍历 C 的右子树 I ABDFECGH

访问 I，I 作为根节点，左右子树为空 ABDFECGHI

方式二

顺序结果

访问 A，依次访问左子树 B，右子树 C，顺序在 A 的后面。 AB_ _ _ C_ _ _

再看 B，访问其左子树 D，右子树 F，顺序在 B 的右面。注意是在上一步 C 的前面
再看 C，访问其左子树 G，右子树 I，顺序在 C 的右面。 ABD* F_C * G_I

再看上一步中的 D、F、G、I，将其左右子树依次排列在节点后面 ABDFEC GH I

顺序	结果
首先访问根节点 A，然后遍历左子树 B	A
访问 B，B 作为根节点，遍历其左子树 D	AB
访问 D，D 作为根节点，左右子树为空，则遍历 B 的右子树 F	ABD
访问 F，F 作为根节点，遍历其左子树 E	ABDF
访问 E，E 作为根节点，左右子树为空，向上遍历 A 的右子树 C	ABDFE
访问 C，C 作为根节点，遍历其左子树 G	ABDFEC
访问 G，G 作为根节点，遍历其左子树，左子树为空，遍历其右子树 H	ABDFECG
访问 H，H 作为根节点，左右子树为空，则遍历 C 的右子树 I	ABDFECGH
访问 I，I 作为根节点，左右子树为空	ABDFECGHI

顺序	结果
访问 A，依次访问左子树 B，右子树 C，顺序在 A 的后面。	AB_ _ _ C_ _ _
再看 B，访问其左子树 D，右子树 F，顺序在 B 的右面。注意是在上一步 C 的前面再看 C，访问其左子树 G，右子树 I，顺序在 C 的右面。	ABD* F_C * G_I
再看上一步中的 D、F、G、I，将其左右子树依次排列在节点后面	ABDFEC GH I

2.4.2、中序遍历

基本思想

中序遍历左子树

访问根节点

中序遍历右子树

遍历结果：DBEFAGHCI

顺序结果

先看 A 节点，因为访问根节点在中间步骤，将 A 放入中间 _ _ _ _ A _ _ _ _

放入 A 的左右子树，左子树 B 在 A 的前面，右子树 C 在 A 的右面
（此时可以看成先访问左子树 B，访问根节点，访问右子树 C） B _ _ _ A _ _ _ C

再看 B，左子树 D 放 B 前面，右子树 F 放在 B 的右边 D _ B _ F _ A _ _C _

同时看 C，左子树 G 放 C 前面，右子树 I 放 C 的右边 D _ B _ F _ A _G _C _ I

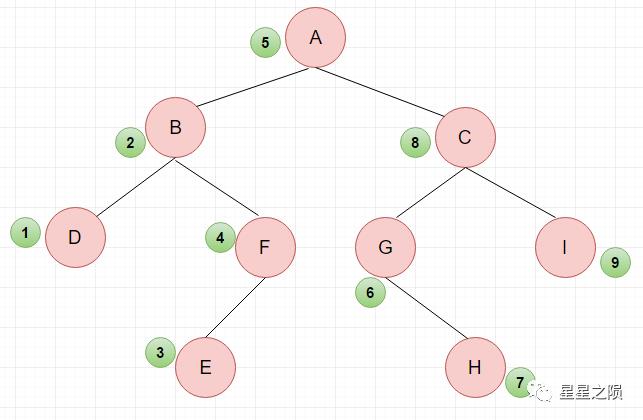
最后将 D、F、G、I 的左右子树分别放在其左右 D _ B E F _ A _GHC _ I

顺序	结果
先看 A 节点，因为访问根节点在中间步骤，将 A 放入中间	_ _ _ _ A _ _ _ _
放入 A 的左右子树，左子树 B 在 A 的前面，右子树 C 在 A 的右面（此时可以看成先访问左子树 B，访问根节点，访问右子树 C）	B _ _ _ A _ _ _ C
再看 B，左子树 D 放 B 前面，右子树 F 放在 B 的右边	D _ B _ F _ A _ _C _
同时看 C，左子树 G 放 C 前面，右子树 I 放 C 的右边	D _ B _ F _ A _G _C _ I
最后将 D、F、G、I 的左右子树分别放在其左右	D _ B E F _ A _GHC _ I

2.4.3、后序遍历

基本思想

后序遍历左子树

后序遍历右子树

访问根节点

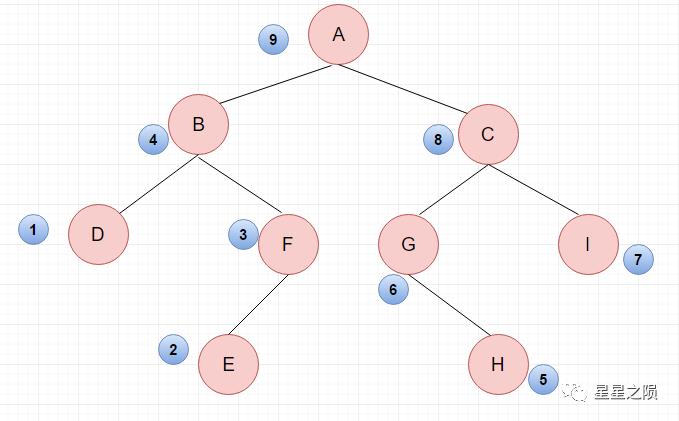
遍历结果：DEFBHGICA

按照前序遍历和中序遍历的思想

顺序结果

先看 A，因为先遍历左子树，再遍历右子树，最后访问根节点。
因此左子树 B 放最左边，右子树 C 放 A 左边。 _ _ __B _ _ C A

再看 B，将 B 的左右子树 D、F 依次放在 B 节点的左边。 _ D _ F _B _ _ C A

再看 C，将 C 的左右子树 G、I 依次放在 C 节点的左边。 _ D _ F _B _ G _I _ C A

再看 D、F、G、I，将其左右子树依次放在对应节点的左边。 D _E _ F _B _H G _I _ C A

顺序	结果
先看 A，因为先遍历左子树，再遍历右子树，最后访问根节点。因此左子树 B 放最左边，右子树 C 放 A 左边。	_ _ __B _ _ C A
再看 B，将 B 的左右子树 D、F 依次放在 B 节点的左边。	_ D _ F _B _ _ C A
再看 C，将 C 的左右子树 G、I 依次放在 C 节点的左边。	_ D _ F _B _ G _I _ C A
再看 D、F、G、I，将其左右子树依次放在对应节点的左边。	D _E _ F _B _H G _I _ C A

2.4.4、层序遍历

基本思想

按照树的层次，自上向下遍历二叉树

每一层次遍历，自左向右遍历。

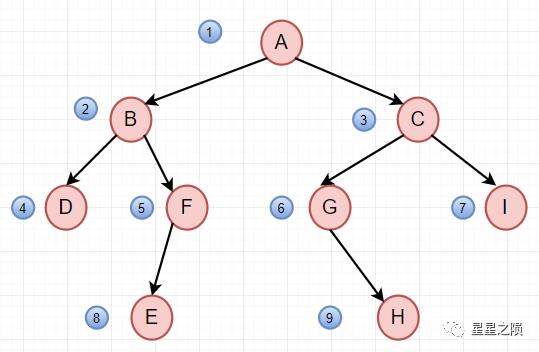
遍历结果：ABCDFGIEH

具体步骤可以省略，即按照顺序遍历即可。

2.5、二叉树的存储结构

2.5.1、顺序存储结构

用一维数组存储二叉树中的节点，并且用节点的存储位置（数组索引）表示节点之间的逻辑关系（父子关系）

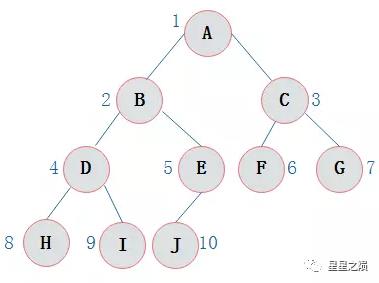
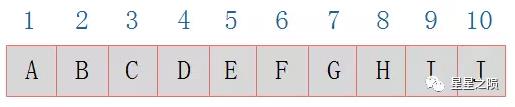
转换为数组存储为：

具体步骤：

将二叉树按照完全二叉树进行编号。根节点的编号为 1，

若某个节点 i 有左孩子，则左孩子的编号为 2i

若某个节点 i 有右孩子，则左孩子的编号为 2i+1

将节点以编号顺序存储到一维数组中。

对于非完全二叉树进行补全子树，空节点也需要进行编号

不完全二叉树

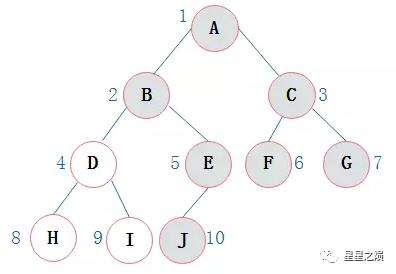
其中浅色结点表示结点不存在。转换成数组后：（∧ 表示数组中此位置没有存储结点。）

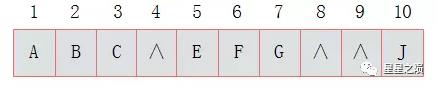
右斜树极端情况：

2.5.2、二叉链表

令二叉树每个节点对应一个链表节点，链表节点除了存放于二叉树节点相关的数据，还有设置指向左右孩子节点的指针。

转换为二叉链表为：

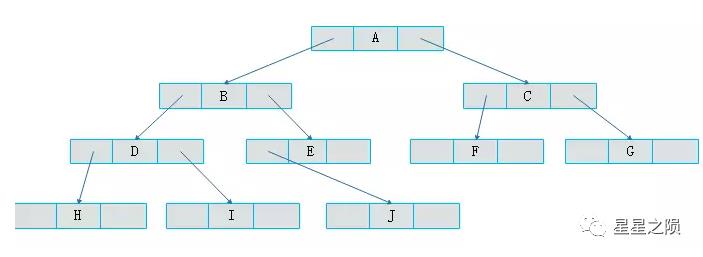
2.6、二叉树创建

二叉树示例：

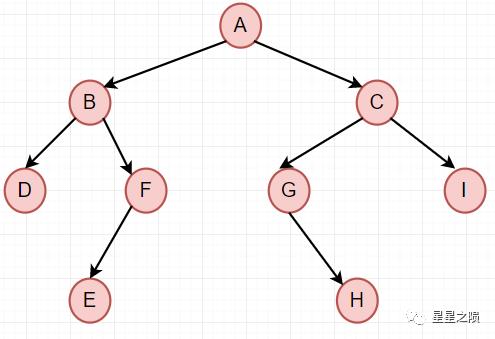
2.6.1、前序遍历创建二叉树

将示例二叉树补全所有节点的左右孩子，空节点使用 null 表示
补全后的二叉树使用前序遍历，转换为一位数组

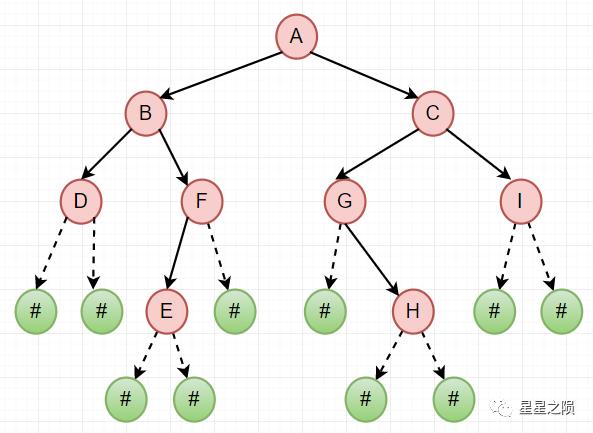
"A", "B", "D", null, null, "F", "E", null, null, null, "C", "G", null, "H",
      null, null, "I", null, null

A	B	D	#	#	F	E	#	#	#	C	G	#	H	#	#	I	#	#
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19

基本思想

创建根节点

取出数组中第一个元素，如果不为空，则 new 一个 TreeNode

如果为空，则该节点为 null，递归结束

递归调用该方法，创建根节点的左孩子，节点数据依次为数组中下一个元素

创建完成后，赋值到根节点的左孩子

递归调用该方法，创建根节点的右孩子，节点数据依次为数组中下一个元素

创建完成后，赋值到根节点的右孩子

全部完成递归，返回值赋值到 root 根节点
public void preCreateTree(List<T> list) {
    this.root = preCreTree(this.root, list);
}
private TreeNode<T> preCreTree(TreeNode<T> node, List<T> list) {
    T t = list.get(LIST_INDEX++);
    if (t == null) {
        node = null;
    } else {
        node = new TreeNode<>(t);
        node.left = preCreTree(node.left, list);
        node.right = preCreTree(node.right, list);
    }
    return node;
}

2.6.2、层序遍历创建二叉树

示例二叉树补全为完全二叉树，完全二叉树的深度与示例二叉树相同，空节点使用 null 表示
补全后的完全二叉树使用层序遍历，转换为一位数组

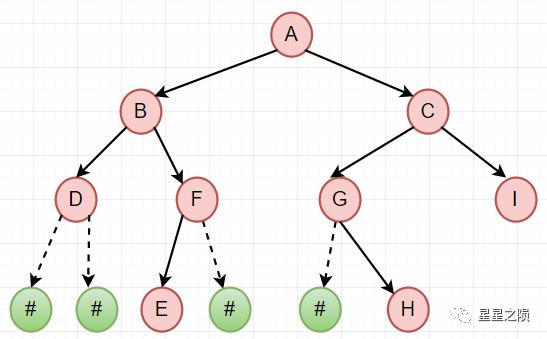
"A", "B", "C", "D", "F", "G", "I", null, null, "E", null, null, "H"

A	B	C	D	F	G	I	#	#	E	#	#	H
1	2	3	4	5	6	7	8	9	10	11	12	13

基本思想

完全二叉树的性质：

对节点数为的完全二叉树进行从上到下按照 1 开始进行层序编号，对应任意节点，

如果节点有左孩子节点，则左孩子节点编号为

如果节点有左孩子节点，则左孩子节点编号为

根据完全二叉树的性质，可以有如下创建步骤：

创建根节点

取出数组中第一个元素，如果不为空，则 new 一个 TreeNode

如果节点下标超出数组长度或者元素为空，则该节点为 null，递归结束

递归调用该方法，创建根节点的左孩子

左孩子节点数据为根节点对应下标的

创建完成后，赋值到根节点的左孩子

递归调用该方法，创建根节点的右孩子

右孩子节点数据为根节点对应下标的

创建完成后，赋值到根节点的右孩子

全部完成递归，返回值赋值到 root 根节点
public void levelCreateTree(List<T> list) {
    this.root = levelCreateTree(this.root, list, LEVEL_LIST_INDEX);
}

private TreeNode<T> levelCreateTree(TreeNode<T> node, List<T> list, int i) {
    if (i > list.size() || list.get(i - 1) == null) {
        node = null;
    } else {
        T t = list.get(i - 1);
        node = new TreeNode<>(t);
        node.left = levelCreateTree(node.left, list, 2 * i);
        node.right = levelCreateTree(node.right, list, 2 * i + 1);
    }
    return node;
}

2.7、二叉树遍历常考考点

对于二叉树的遍历有一类典型题型。

1）已知前序遍历序列和中序遍历序列，确定一棵二叉树。

例题：

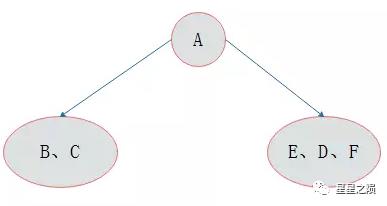
若一棵二叉树的前序遍历为 ABCDEF，中序遍历为 CBAEDF，请画出这棵二叉树。

分析：

前序遍历第一个输出结点为根结点，故 A 为根结点。

而中序遍历中，根结点处于左右子树结点中间，故结点 A 的左子树中结点有 CB，右子树中结点有 EDF。

按照同样的分析方法，对 A 的左右子树进行划分，最后得出二叉树的形态

2）已知后序遍历序列和中序遍历序列，确定一棵二叉树。

后序遍历中最后访问的为根结点，因此可以按照上述同样的方法，找到根结点后分成两棵子树，进而继续找到子树的根结点，一步步确定二叉树的形态。

注：已知前序遍历序列和后序遍历序列，不可以唯一确定一棵二叉树。

2.8、二叉树非递归遍历

2.8.1、前序遍历

基本思路

（1）对于节点 node，判断 node 是否为空。

（2）如果 node 不为空，访问 node 节点数据。

将节点 node 压入栈

将节点 node 的左节点赋值给 node：node=node.left

重复（1）操作，此时（1）中的 node 为之前节点的左节点

（3）如果 node 节点为空，并且栈中有数据

弹出栈顶节点，并赋值到 node

将栈顶节点（node）的右节点赋值到 node：node=node.right

重复（1）操作，此时（1）中的 node 为栈顶节点的右节点

（4）如果 node 节点为空，并且栈中无数据，结束循环遍历。

示例二叉树:

前序遍历结果：ABDFECGHI

针对示例步骤

节点 node=A，node 节点不为空，访问 node 数据 A，压入栈中，赋值 A 的左节点给 node，则 node=B

栈：A

输出：A

节点 node=B，node 节点不为空，访问 node 数据 B，压入栈中，赋值 B 的左节点给 node，则 node=D

栈：BA

输出：AB

节点 node=D，node 节点不为空，访问 node 数据 D，压入栈中，赋值 D 的左节点给 node，则 node=null

栈：DBA

输出：ABD

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=D，栈顶节点（node）的右节点赋值到 node=D.right=null

栈：BA

输出：ABD

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=B，栈顶节点（node）的右节点赋值到 node=B.right=F

栈：A

输出：ABD

节点 node=F，node 节点不为空，访问 node 数据 F，压入栈中，赋值 F 的左节点给 node，则 node=E

栈：FA

输出：ABDF

节点 node=E，node 节点不为空，访问 node 数据 E，压入栈中，赋值 E 的左节点给 node，则 node=null

栈：EFA

输出：ABDFE

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=E，栈顶节点（node）的右节点赋值到 node=E.right=null

栈：FA

输出：ABDFE

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=F，栈顶节点（node）的右节点赋值到 node=F.right=null

栈：A

输出：ABDFE

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=A，栈顶节点（node）的右节点赋值到 node=A.right=C

栈：

输出：ABDFE

节点 node=C，node 节点不为空，访问 node 数据 C，压入栈中，赋值 D 的左节点给 node，则 node=G

栈：C

输出：ABDFEC

节点 node=G，node 节点不为空，访问 node 数据 G，压入栈中，赋值 D 的左节点给 node，则 node=null

栈：GC

输出：ABDFECG

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=G，栈顶节点（node）的右节点赋值到 node=G.right=H

栈：C

输出：ABDFECG

节点 node=H，node 节点不为空，访问 node 数据 H，压入栈中，赋值 H 的左节点给 node，则 node=null

栈：HC

输出：ABDFECGH

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=H，栈顶节点（node）的右节点赋值到 node=H.right=null

栈：C

输出：ABDFECGH

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=C，栈顶节点（node）的右节点赋值到 node=C.right=I

栈：

输出：ABDFECGH

节点 node=I，node 节点不为空，访问 node 数据 I，压入栈中，赋值 H 的左节点给 node，则 node=null

栈：I

输出：ABDFECGHI

节点 node=null，node 节点为空，并且栈中无数据，结束循环遍历。

示例代码：

public void preOrderNoRecursion() {
    if (this.root == null) {
        return;
    }
    TreeNode<T> node = this.root;
    Stack<TreeNode<T>> stack = new Stack<>();
    while (node != null || !stack.empty()) {
        if (node != null) {
            System.out.print(node.data + "\t");
            stack.push(node);
            node = node.left;
        } else {
            node = stack.pop();
            node = node.right;
        }
    }
}

方案二：*参考

public void preOrderNoRecursion2() {
    if (this.root == null) {
        return;
    }
    TreeNode<T> node = this.root;
    Stack<TreeNode<T>> stack = new Stack<>();
    stack.push(node);
    while (!stack.empty() && node != null) {
        System.out.print(node.data + "\t");
        if (node.right != null) {
            stack.push(node.right);
        }
        if (node.left != null) {
            node = node.left;
        } else {
            node = stack.pop();
        }
    }
}

2.8.2、中序遍历

基本思路

（1）对于节点 node，判断 node 是否为空

（2）如果 node 不为空

将 node 节点压入栈

将 node 节点的左节点赋值给 node：node=node.left

重复（1）操作，此时（1）中的 node 为之前节点的左节点。

（3）如果 node 节点为空，兵器栈中有数据

弹出栈顶节点，并赋值到 node

访问栈顶节点（node）的数据

将栈顶节点（node）的右节点赋值给 node：node=node.right

重复（1）操作，此时（1）中的 node 为栈顶节点的右节点

（4）如果 node 节点为空，并且栈中无数据，结束循环遍历。

示例二叉树:

中序遍历结果：DBEFAGHCI

针对示例步骤

节点 node=A，node 节点不为空，压入栈中，赋值 A 的左节点给 node，则 node=A.left=B

栈：A

输出：

节点 node=B，node 节点不为空，压入栈中，赋值 B 的左节点给 node，则 node=B.left=D

栈：BA

输出：

节点 node=D，node 节点不为空，压入栈中，赋值 D 的左节点给 node，则 node=D.left=null

栈：DBA

输出：

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=D，访问栈顶节点数据 D，栈顶节点（node）的右节点赋值到 node=D.right=null

栈：BA

输出：D

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=B，访问栈顶节点数据 B，栈顶节点（node）的右节点赋值到 node=B.right=F

栈：A

输出：DB

节点 node=F，node 节点不为空，压入栈中，赋值 D 的左节点给 node，则 node=F.left=E

栈：FA

输出：DB

节点 node=E，node 节点不为空，压入栈中，赋值 E 的左节点给 node，则 node=E.left=null

栈：EFA

输出：DB

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=E，访问栈顶节点数据 E，栈顶节点（node）的右节点赋值到 node=E.right=null

栈：FA

输出：DBE

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=F，访问栈顶节点数据 F，栈顶节点（node）的右节点赋值到 node=F.right=null

栈：A

输出：DBEF

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=A，访问栈顶节点数据 A，栈顶节点（node）的右节点赋值到 node=A.right=C

栈：

输出：DBEFA

节点 node=C，node 节点不为空，压入栈中，赋值 C 的左节点给 node，则 node=C.left=G

栈：C

输出：DBEFA

节点 node=G，node 节点不为空，压入栈中，赋值 G 的左节点给 node，则 node=G.left=null

栈：GC

输出：DBEFA

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=G，访问栈顶节点数据 G，栈顶节点（node）的右节点赋值到 node=G.right=H

栈：C

输出：DBEFAG

节点 node=H，node 节点不为空，压入栈中，赋值 H 的左节点给 node，则 node=H.left=null

栈：HC

输出：DBEFAG

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=H，访问栈顶节点数据 H，栈顶节点（node）的右节点赋值到 node=H.right=null

栈：C

输出：DBEFAGH

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=C，访问栈顶节点数据 C，栈顶节点（node）的右节点赋值到 node=C.right=I

栈：

输出：DBEFAGHC

节点 node=I，node 节点不为空，压入栈中，赋值 I 的左节点给 node，则 node=I.left=null

栈：I

输出：DBEFAGHC

节点 node=null，node 节点为空，并且栈中有数据。弹栈赋值 node=I，访问栈顶节点数据 I，栈顶节点（node）的右节点赋值到 node=I.right=null

栈：

输出：DBEFAGHCI

节点 node=null，node 节点为空，并且栈中无数据，结束循环遍历。

2.8.3、后序遍历

示例二叉树:

基本思路

思路一

对于任一结点 P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问，因此其右孩子还为被访问。

所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。

这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

（1）判断节点 node 是否为空

（2）如果 node 节点不为空，则压入栈。

赋值左节点给 node：node=node.left

重复（1）操作，此时 node 为上一个节点的左节点。（将 node 的左子树都压入栈）

（3）如果 node 节点为空，即已经将最初 node 的左子树压入栈。在栈不为空的情况下：

此时 node 为遍历到树左侧最后一个左节点的空左节点了。

取出栈顶节点，并非弹栈，赋值给 node

此时 node 为遍历到树左侧最后一个左节点

（4）如果栈顶节点右子树为空，或者栈顶节点的右子树是否已经被访问

访问栈顶节点 node 数据，弹栈。

由（3）可知，节点 node 的左子树为空。此时右子树为空或已经被访问，则可以访问到此 node 节点。

记录被访问的节点 temp = node;

设置 node 为空

（5）如果栈顶节点右子树不为空，并且还未被访问

赋值栈顶节点右节点给 node：node = node.right;

重复（1）接着（2）操作，压入栈。
代码示例：
/**
 * 非递归后序遍历
 */
public void backOrderNoRecursion() {
 if (this.root == null) {
  return;
 }
 System.out.print("[");
 TreeNode<T> node = this.root;
 TreeNode<T> temp = null;
 Stack<TreeNode<T>> stack = new Stack<>();
 while (node != null || !stack.empty()) {
  // 沿左子树一直往下搜索，直至出现没有左子树的结点
  while (node != null) {
   stack.push(node);
   node = node.left;
  }
  if (!stack.empty()) {
   node = stack.peek();
   // 如果栈顶元素的右子树为空，或者栈顶节点的右孩子为刚访问过得节点，则退栈并访问
   if (node.right == null || node.right == temp) {
    System.out.print(node.data + "\t");
    stack.pop();
    // 记录最近访问的节点
    temp = node;
    node = null;
   } else {
    node = node.right;
   }
  }
 }
 System.out.println("]");
}
思路二

要保证根结点在左孩子和右孩子访问之后才能访问，因此对于任一结点 P，先将其入栈。

如果 P 不存在左孩子和右孩子，则可以直接访问它；或者 P 存在左孩子或者右孩子，但是其左孩子和右孩子都已被访问过了，则同样可以直接访问该结点。

若非上述两种情况，则将 P 的右孩子和左孩子依次入栈，这样就保证了每次取栈顶元素的时候，左孩子在右孩子前面被访问，左孩子和右孩子都在根结点前面被访问。

首先将节点 node 压入栈

（1）判断栈是否为空，赋值 node 为栈顶节点，但是不弹栈

（2）如果栈顶节点（node）左右节点为空，或者 node 节点的左右节点中任一个为上一个被访问节点

访问节点 node 数据

弹栈

记录 temp 为本次访问的节点

重复（1）操作

（3）如果 node 左右节点不为空，并且 node 左右节点并非上一次访问的节点

如果 node 右节点不为空，压入栈 node.right

如果 node 左节点不为空，压入栈 node.left

重复（1）操作，此时的栈顶节点为 node 的左右节点。
代码示例：
public void backOrderNoRecursion2() {
 if (this.root == null) {
  return;
 }
 System.out.print("[");
 TreeNode<T> node = this.root;
 TreeNode<T> temp = null;
 Stack<TreeNode<T>> stack = new Stack<>();
 stack.push(node);
 while (!stack.empty()) {
  node = stack.peek();
  if ((node.left == null && node.right == null)
    || (temp != null && (temp == node.left || temp == node.right))) {
   System.out.print(node.data + "\t");
   stack.pop();
   temp = node;
  } else {
   if (node.right != null) {
    stack.push(node.right);
   }
   if (node.left != null) {
    stack.push(node.left);
   }
  }
 }
 System.out.println("]");
}

非递归遍历参考

https://www.cnblogs.com/zl1991/p/6952587.html

https://blog.csdn.net/z_ryan/article/details/80854233

https://www.cnblogs.com/SHERO-Vae/p/5800363.html

专题：https://xiaozhuanlan.com/topic/5036471892

2.9、二叉树 Java 实现

2.9.1、BinaryTree

API：

BinaryTree()：构造方法

BinaryTree(T data)：带参数构造方法

void releaseTree()：释放二叉树

TreeNode getRoot()：获取根节点

BinaryTree getLeftChildTree(T t)：根据节点数据获取该节点的左子树

BinaryTree getRightChildTree(T t)：根据节点数据获取该节点的右子树

BinaryTree getBTree(T t)：根据节点数据获取当前树

int getLeafNum()：获取叶子节点数目

int getNodeNum()：获取节点个数

int getTreeDepth()：获取树的深度

void setLeftTree(BinaryTree tree)：设置左子树

void setRightTree(BinaryTree tree)：设置右子树

void levelCreateTree(List list)：层序遍历创建二叉树

void preCreateTree(List list)：前序创建二叉树

void preOrder()：前序遍历

void midOrder()：中序遍历

void backOrder()：后序遍历

void levelOrder()：层序遍历二叉树

void preOrderNoRecursion()：非递归前序遍历

void preOrderNoRecursion2()：非递归前序遍历 2

void midOrderNoRecursion()：非递归中序遍历

void backOrderNoRecursion()：非递归后序遍历

void backOrderNoRecursion2()：非递归后序遍历 2

source code：

package com.starfall.tree;

import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
import java.util.Stack;

public class BinaryTree<T> {

 private TreeNode<T> root;
 private int LIST_INDEX = 0;

 public BinaryTree() {
  root = new TreeNode<>();
 }

 public BinaryTree(T data) {
  root = new TreeNode<>();
  root.data = data;
 }

 private BinaryTree(TreeNode<T> node) {
  this.root = node;
 }

 /**
  * 释放树
  */
 public void releaseTree() {
  releaseTree(this.root);
 }

 private void releaseTree(TreeNode<T> node) {
  if (node != null) {
   releaseTree(node.left);
   releaseTree(node.right);
   node = null;
  }
 }

 /**
  * 获取根节点
  *
  * @return 根节点
  */
 public TreeNode<T> getRoot() {
  return this.root;
 }

 /**
  * 根据节点数据获取该节点的左子树
  *
  * @param t
  *            节点数据
  * @return 左子树
  */
 public BinaryTree<T> getLeftChildTree(T t) {
  TreeNode<T> node = getNodeByValue(this.root, t);
  if (node == null) {
   return null;
  } else {
   return new BinaryTree<>(node.left);
  }
 }

 /**
  * 根据节点数据获取该节点的右子树
  *
  * @param t
  *            节点数据
  * @return 右子树
  */
 public BinaryTree<T> getRightChildTree(T t) {
  TreeNode<T> node = getNodeByValue(this.root, t);
  if (node == null) {
   return null;
  } else {
   return new BinaryTree<>(node.right);
  }
 }

 /**
  * 根据节点数据获取当前树
  *
  * @param t
  *            节点数据
  * @return 子树
  */
 public BinaryTree<T> getBTree(T t) {
  TreeNode<T> node = getNodeByValue(this.root, t);
  if (node == null) {
   return null;
  } else {
   return new BinaryTree<>(node);
  }
 }

 private TreeNode<T> getNodeByValue(TreeNode<T> node, T t) {
  if (node == null) {
   return null;
  } else if (node.data == t) {
   return node;
  } else {
   return getNodeByValue(node.left, t) == null ? getNodeByValue(node.right, t) : getNodeByValue(node.left, t);
  }
 }

 /**
  * 获取叶子节点数目
  *
  * @return 叶子节点数目
  */
 public int getLeafNum() {
  return getLeafNum(this.root);
 }

 private int getLeafNum(TreeNode<T> node) {
  if (node == null) {
   return 0;
  } else if (node.left == null && node.right == null) {
   return 1;
  } else {
   return getLeafNum(node.left) + getLeafNum(node.right);
  }

 }

 /**
  * 获取节点个数
  *
  * @return 节点个数
  */
 public int getNodeNum() {
  return getNodeNum(this.root);
 }

 private int getNodeNum(TreeNode<T> node) {
  if (node == null) {
   return 0;
  }
  return getNodeNum(node.left) + getNodeNum(node.right) + 1;
 }

 /**
  * 获取树的深度
  *
  * @return 树的深度
  */
 public int getTreeDepth() {
  return getTreeDepth(this.root);
 }

 private int getTreeDepth(TreeNode<T> node) {
  if (node == null) {
   return 0;
  }
  int leftDepth = getTreeDepth(node.left) + 1;
  int rightDepth = getTreeDepth(node.right) + 1;
  return leftDepth > rightDepth ? leftDepth : rightDepth;
 }

 /**
  * 设置左子树
  *
  * @param tree
  *            左子树
  */
 public void setLeftTree(BinaryTree<T> tree) {
  this.root.left = tree.root;
 }

 /**
  * 设置右子树
  *
  * @param tree
  *            右子树
  */
 public void setRightTree(BinaryTree<T> tree) {
  this.root.right = tree.root;
 }

 /**
  * 层序遍历创建二叉树
  *
  * @param list
  *            list参数
  */
 public void levelCreateTree(List<T> list) {
  this.root = levelCreateTree(list, 1);
 }

 private TreeNode<T> levelCreateTree(List<T> list, int i) {
  TreeNode<T> node;
  if (i > list.size() || list.get(i - 1) == null) {
   node = null;
  } else {
   T t = list.get(i - 1);
   node = new TreeNode<>(t);
   node.left = levelCreateTree(list, 2 * i);
   node.right = levelCreateTree(list, 2 * i + 1);
  }
  return node;
 }

 // private TreeNode<T> levelCreateTree(TreeNode<T> node, List<T> list, int i) {
 // if (i > list.size() || list.get(i - 1) == null) {
 // node = null;
 // } else {
 // T t = list.get(i - 1);
 // node = new TreeNode<>(t);
 // node.left = levelCreateTree(node.left, list, 2 * i);
 // node.right = levelCreateTree(node.right, list, 2 * i + 1);
 // }
 // return node;
 // }

 /**
  * 前序创建二叉树
  *
  * @param list
  *            list参数
  */
 public void preCreateTree(List<T> list) {
  this.root = preCreTree(list);
 }

 private TreeNode<T> preCreTree(List<T> list) {
  T t = list.get(LIST_INDEX++);
  TreeNode<T> node;
  if (t == null) {
   node = null;
  } else {
   node = new TreeNode<>(t);
   node.left = preCreTree(list);
   node.right = preCreTree(list);
  }
  return node;
 }

 // private TreeNode<T> preCreTree(TreeNode<T> node, List<T> list) {
 // T t = list.get(LIST_INDEX++);
 // if (t == null) {
 // node = null;
 // } else {
 // node = new TreeNode<>(t);
 // node.left = preCreTree(node.left, list);
 // node.right = preCreTree(node.right, list);
 // }
 // return node;
 // }

 /**
  * 前序遍历
  */
 public void preOrder() {
  System.out.print("[");
  preOrder(this.root);
  System.out.println("]");
 }

 private void preOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  System.out.print(node.data + "\t");
  preOrder(node.left);
  preOrder(node.right);
 }

 /**
  * 中序遍历
  */
 public void midOrder() {
  System.out.print("[");
  midOrder(this.root);
  System.out.println("]");
 }

 private void midOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  midOrder(node.left);
  System.out.print(node.data + "\t");
  midOrder(node.right);
 }

 /**
  * 后序遍历
  */
 public void backOrder() {
  System.out.print("[");
  backOrder(this.root);
  System.out.println("]");
 }

 private void backOrder(TreeNode<T> node) {
  if (node == null) {
   return;
  }
  backOrder(node.left);
  backOrder(node.right);
  System.out.print(node.data + "\t");
 }

 /**
  * 层序遍历二叉树
  */
 public void levelOrder() {
  System.out.print("[");
  levelOrder(this.root);
  System.out.println("]");
 }

 private void levelOrder(TreeNode<T> node) {
  Queue<TreeNode<T>> q = new LinkedList<>();
  q.offer(node);
  while (!q.isEmpty()) {
   TreeNode<T> temp = q.poll();
   if (temp == null) {
    return;
   }
   System.out.print(temp.data + "\t");
   if (temp.left != null) {
    q.offer(temp.left);
   }
   if (temp.right != null) {
    q.offer(temp.right);
   }
  }
 }

 /**
  * 非递归前序遍历
  */
 public void preOrderNoRecursion() {
  if (this.root == null) {
   return;
  }
  System.out.print("[");
  TreeNode<T> node = this.root;
  Stack<TreeNode<T>> stack = new Stack<>();
  while (node != null || !stack.empty()) {
   if (node != null) {
    System.out.print(node.data + "\t");
    stack.push(node);
    node = node.left;
   } else {
    node = stack.pop();
    node = node.right;
   }
  }
  System.out.println("]");
 }

 /**
  * 非递归前序遍历2
  */
 public void preOrderNoRecursion2() {
  if (this.root == null) {
   return;
  }
  System.out.print("[");
  TreeNode<T> node = this.root;
  Stack<TreeNode<T>> stack = new Stack<>();
  stack.push(node);
  while (!stack.empty() && node != null) {
   System.out.print(node.data + "\t");
   if (node.right != null) {
    stack.push(node.right);
   }
   if (node.left != null) {
    node = node.left;
   } else {
    node = stack.pop();
   }
  }
  System.out.println("]");
 }

 /**
  * 非递归中序遍历
  */
 public void midOrderNoRecursion() {
  if (this.root == null) {
   return;
  }
  System.out.print("[");
  TreeNode<T> node = this.root;
  Stack<TreeNode<T>> stack = new Stack<>();
  while (!stack.empty() || node != null) {
   if (node != null) {
    stack.push(node);
    node = node.left;
   } else {
    node = stack.pop();
    System.out.print(node.data + "\t");
    node = node.right;
   }
  }
  System.out.println("]");
 }

 /**
  * 非递归后序遍历
  */
 public void backOrderNoRecursion() {
  if (this.root == null) {
   return;
  }
  System.out.print("[");
  TreeNode<T> node = this.root;
  TreeNode<T> temp = null;
  Stack<TreeNode<T>> stack = new Stack<>();
  while (node != null || !stack.empty()) {
   // 沿左子树一直往下搜索，直至出现没有左子树的结点
   while (node != null) {
    stack.push(node);
    node = node.left;
   }
   if (!stack.empty()) {
    node = stack.peek();
    // 如果栈顶元素的右子树为空，或者栈顶节点的右孩子为刚访问过得节点，则退栈并访问
    if (node.right == null || node.right == temp) {
     System.out.print(node.data + "\t");
     stack.pop();
     // 记录最近访问的节点
     temp = node;
     node = null;
    } else {
     node = node.right;
    }
   }
  }
  System.out.println("]");
 }

 public void backOrderNoRecursion2() {
  if (this.root == null) {
   return;
  }
  System.out.print("[");
  TreeNode<T> node = this.root;
  TreeNode<T> temp = null;
  Stack<TreeNode<T>> stack = new Stack<>();
  stack.push(node);
  while (!stack.empty()) {
   node = stack.peek();
   if ((node.left == null && node.right == null)
     || (temp != null && (temp == node.left || temp == node.right))) {
    System.out.print(node.data + "\t");
    stack.pop();
    temp = node;
   } else {
    if (node.right != null) {
     stack.push(node.right);
    }
    if (node.left != null) {
     stack.push(node.left);
    }
   }
  }
  System.out.println("]");
 }

 public static class TreeNode<T> {
  private TreeNode<T> left;
  private TreeNode<T> right;
  private T data;

  public TreeNode() {

  }

  public TreeNode(T data) {
   this.data = data;
  }

  public TreeNode<T> getLeft() {
   return left;
  }

  public TreeNode<T> getRight() {
   return right;
  }

  public T getData() {
   return data;
  }
 }
}

2.9.3、BinaryTreeTest

示例二叉树:

package com.starfall.tree;

import org.junit.Test;

import java.util.Arrays;
import java.util.List;

public class BinaryTreeTest {

 /**
  * 添加子树创建二叉树
  */
 @Test
 public void test01() {
   System.out.println("添加子树创建二叉树");
  // 层序遍历：ABCDEFG
  // 根节点
  BinaryTree<String> btree = new BinaryTree<>("A");
  // 根节点左右子树
  BinaryTree<String> bt1, bt2;
  bt1 = new BinaryTree<>("B");
  btree.setLeftTree(bt1);
  bt2 = new BinaryTree<>("C");
  btree.setRightTree(bt2);
  // B左右子树
  BinaryTree<String> bt11, bt12;
  bt11 = new BinaryTree<>("D");
  bt1.setLeftTree(bt11);
  bt12 = new BinaryTree<>("E");
  bt1.setRightTree(bt12);
  // C左右子树
  BinaryTree<String> bt21, bt22;
  bt21 = new BinaryTree<>("F");
  bt2.setLeftTree(bt21);
  bt22 = new BinaryTree<>("G");
  bt2.setRightTree(bt22);
  // 遍历
  btree.preOrder();
  btree.midOrder();
  btree.backOrder();
  btree.levelOrder();
  btree.releaseTree();
  System.out.println("**********添加子树创建二叉树**********end");
 }

 /**
  * 前序遍历创建二叉树
  */
 @Test
 public void test02() {
  System.out.println("前序遍历创建二叉树");
  // 补全空节点
  List<String> list = Arrays.asList("A", "B", "D", null, null, "F", "E", null, null, null, "C", "G", null, "H",
    null, null, "I", null, null);
  BinaryTree<String> bt = new BinaryTree<>();
  bt.preCreateTree(list);
  bt.preOrder();
  bt.midOrder();
  bt.backOrder();
  bt.levelOrder();
  bt.releaseTree();
  System.out.println("**********前序遍历创建二叉树**********end");
 }

 /**
  * 层序遍历创建二叉树
  */
 @Test
 public void test03() {
  System.out.println("层序遍历创建二叉树");
  // 补全空节点，转为完全二叉树
  List<String> list = Arrays.asList("A", "B", "C", "D", "F", "G", "I", null, null, "E", null, null, "H");
  BinaryTree<String> bt = new BinaryTree<>();
  bt.levelCreateTree(list);
  bt.preOrder();
  bt.midOrder();
  bt.backOrder();
  bt.levelOrder();
  bt.releaseTree();
  System.out.println("**********层序遍历创建二叉树**********end");
 }

 /**
  * 二叉树其他用法1
  */
 @Test
 public void test04() {
  System.out.println("二叉树其他用法1");
  // 前序遍历创建二叉树
  List<String> list = Arrays.asList("A", "B", "D", null, null, "F", "E", null, null, null, "C", "G", null, "H",
    null, null, "I", null, null);
  BinaryTree<String> bt = new BinaryTree<>();
  bt.preCreateTree(list);
  System.out.println(bt.getNodeNum());
  System.out.println(bt.getTreeDepth());
  System.out.println(bt.getLeafNum());
  bt.preOrder();
  bt.midOrder();
  bt.backOrder();
  bt.levelOrder();
  System.out.println("*******根据节点数据获取当前树*****");
  BinaryTree<String> tree = bt.getBTree("F");
  System.out.println(tree.getNodeNum());
  System.out.println(tree.getTreeDepth());
  System.out.println(tree.getLeafNum());
  System.out.println(tree.getRoot().getData());
  tree.levelOrder();
  bt.releaseTree();
  tree.releaseTree();
  System.out.println("**********二叉树其他用法1**********end");
 }

 /**
  * 二叉树其他用法2
  */
 @Test
 public void test05() {
  System.out.println("二叉树其他用法2");
  // 前序遍历创建二叉树
  List<String> list = Arrays.asList("A", "B", "D", null, null, "F", "E", null, null, null, "C", "G", null, "H",
    null, null, "I", null, null);
  BinaryTree<String> bt = new BinaryTree<>();
  bt.preCreateTree(list);
  System.out.println("*******根据节点数据获取左子树*****");
  BinaryTree<String> leftChildTree = bt.getLeftChildTree("D");
  leftChildTree.preOrder();
  leftChildTree.midOrder();
  leftChildTree.backOrder();
  leftChildTree.levelOrder();
  System.out.println("*******根据节点数据获取右子树*****");
  BinaryTree<String> rightChildTree = bt.getRightChildTree("A");
  rightChildTree.preOrder();
  rightChildTree.midOrder();
  rightChildTree.backOrder();
  rightChildTree.levelOrder();
  System.out.println("**********二叉树其他用法2**********end");
 }

 /**
  * 非递归遍历
  */
 @Test
 public void test06() {
  // 前序遍历创建二叉树
  List<String> list = Arrays.asList("A", "B", "D", null, null, "F", "E", null, null, null, "C", "G", null, "H",
    null, null, "I", null, null);
  BinaryTree<String> bt = new BinaryTree<>();
  bt.preCreateTree(list);
  System.out.println("*******前序遍历******");
  bt.preOrder();
  bt.preOrderNoRecursion();
  bt.preOrderNoRecursion2();
  System.out.println("*******中序遍历******");
  bt.midOrder();
  bt.midOrderNoRecursion();
  System.out.println("*******后序遍历******");
  bt.backOrder();
  bt.backOrderNoRecursion();
  bt.backOrderNoRecursion2();
 }
}

以上是关于二二叉树的主要内容，如果未能解决你的问题，请参考以下文章

树与二叉树

二叉树与链表之间的转换

NC41 最长无重复子数组/NC133链表的奇偶重排/NC116把数字翻译成字符串/NC135 股票交易的最大收益/NC126换钱的最少货币数/NC45实现二叉树先序，中序和后序遍历（递归）(代码片段

osgEarth的Rex引擎原理分析（一二二）着色器程序的opengl过程

北邮数据结构考研——平衡二叉树LR型失衡

数据结构二叉树