非线性整数规划的遗传算法Matlab程序

Posted 2022-08-24 之墨_

非线性整数规划的遗传算法Matlab程序

通常，非线性整数规划是一个具有指数复杂度的NP问题，如果约束较为复杂，Matlab优化工具箱和一些优化软件比如lingo等，常常无法应用，即使能应用也不能给出一个较为令人满意的解。这时就需要针对问题设计专门的优化算法。下面举一个遗传算法应用于非线性整数规划的编程实例，供大家参考！
模型的形式和适应度函数定义如下：

这是一个具有200个01决策变量的多目标非线性整数规划，编写优化的目标函数如下，其中将多目标转化为单目标采用简单的加权处理。

function Fitness=FITNESS(x,FARM,e,q,w)
%% 适应度函数
%  输入参数列表
%  x        决策变量构成的4×50的0-1矩阵
%  FARM     细胞结构存储的当前种群，它包含了个体x
%  e        4×50的系数矩阵
%  q        4×50的系数矩阵
%  w        1×50的系数矩阵
%%
gamma=0.98;
N=length(FARM);%种群规模
F1=zeros(1,N);
F2=zeros(1,N);
for i=1:N
    xx=FARMi;
    ppp=(1-xx)+(1-q).*xx;
    F1(i)=sum(w.*prod(ppp));
    F2(i)=sum(sum(e.*xx));
end
ppp=(1-x)+(1-q).*x;
f1=sum(w.*prod(ppp));
f2=sum(sum(e.*x));
Fitness=gamma*sum(min([sign(f1-F1);zeros(1,N)]))+(1-gamma)*sum(min([sign(f2-F2);zeros(1,N)]));

针对问题设计的遗传算法

其中对模型约束的处理是重点考虑的地方

function [Xp,LC1,LC2,LC3,LC4]=MYGA(M,N,Pm)
%% 求解01整数规划的遗传算法
%% 输入参数列表
%  M     遗传进化迭代次数
%  N     种群规模
%  Pm    变异概率
%% 输出参数列表
%  Xp    最优个体
%  LC1   子目标1的收敛曲线
%  LC2   子目标2的收敛曲线
%  LC3   平均适应度函数的收敛曲线
%  LC4   最优适应度函数的收敛曲线
%% 参考调用格式[Xp,LC1,LC2,LC3,LC4]=MYGA(50,40,0.3)

第一步：载入数据和变量初始化

%% 第一步：载入数据和变量初始化
load eqw;%载入三个系数矩阵e,q,w
%输出变量初始化
Xp=zeros(4,50);
LC1=zeros(1,M);
LC2=zeros(1,M);
LC3=zeros(1,M);
LC4=zeros(1,M);
Best=inf;

%% 第二步：随机产生初始种群
farm=cell(1,N);%用于存储种群的细胞结构
k=0;
while k    %以下是一个合法个体的产生过程
    x=zeros(4,50);%x每一列的1的个数随机决定
    for i=1:50
        R=rand;
        Col=zeros(4,1);
        if R<0.7
            RP=randperm(4);%1的位置也是随机的
            Col(RP(1))=1;
        elseif R>0.9
            RP=randperm(4);
            Col(RP(1:2))=1;
        else
            RP=randperm(4);
            Col(RP(1:3))=1;
        end
        x(:,i)=Col;
    end
    %下面是检查行和是否满足约束的过程，对于不满足约束的予以抛弃
    Temp1=sum(x,2);
    Temp2=find(Temp1>20);
    if length(Temp2)==0
        k=k+1;
        farmk=x;
    end
end

以下是进化迭代过程

第三步：交叉

%% 以下是进化迭代过程

counter=0;%设置迭代计数器
while counter

%% 第三步：交叉
 %交叉采用双亲双子单点交叉
 newfarm=cell(1,2*N);%用于存储子代的细胞结构
 Ser=randperm(N);%两两随机配对的配对表
 A=farmSer(1);%取出父代A
 B=farmSer(2);%取出父代B
 P0=unidrnd(49);%随机选择交叉点
 a=[A(:,1:P0),B(:,(P0+1):end)];%产生子代a
 b=[B(:,1:P0),A(:,(P0+1):end)];%产生子代b
 newfarm2*N-1=a;%加入子代种群
 newfarm2*N=b;
 %以下循环是重复上述过程
 for i=1:(N-1)
     A=farmSer(i);
     B=farmSer(i+1);
     P0=unidrnd(49);
     a=[A(:,1:P0),B(:,(P0+1):end)];
     b=[B(:,1:P0),A(:,(P0+1):end)];
     newfarm2*i-1=a;
     newfarm2*i=b;
 end
 FARM=[farm,newfarm];%新旧种群合并

第四步：选择复制

%% 第四步：选择复制
    FLAG=ones(1,3*N);%标志向量，对是否满足约束进行标记
    %以下过程是检测新个体是否满足约束
    for i=1:(3*N)
        x=FARMi;
        sum1=sum(x,1);
        sum2=sum(x,2);
        flag1=find(sum1==0);
        flag2=find(sum1==4);
        flag3=find(sum2>20);
        if length(flag1)+length(flag2)+length(flag3)>0
            FLAG(i)=0;%如果不满足约束，用0加以标记
        end
    end
    NN=length(find(FLAG)==1);%满足约束的个体数目，它一定大于等于N
    NEWFARM=cell(1,NN);
    %以下过程是剔除不满主约束的个体
    kk=0;
    for i=1:(3*N)
        if FLAG(i)==1
            kk=kk+1;
            NEWFARMkk=FARMi;
        end
    end
    %以下过程是计算并存储当前种群每个个体的适应值
    SYZ=zeros(1,NN);
    syz=zeros(1,N);
    for i=1:NN
        x=NEWFARMi;
        SYZ(i)=FITNESS2(x,NEWFARM,e,q,w);%调用适应值子函数
    end
    k=0;
    %下面是选择复制，选择较优的N个个体复制到下一代
    while k        minSYZ=min(SYZ);
        posSYZ=find(SYZ==minSYZ);
        POS=posSYZ(1);
        k=k+1;
        farmk=NEWFARMPOS;
        syz(k)=SYZ(POS);
        SYZ(POS)=inf;
    end
    %记录和更新，更新最优个体，记录收敛曲线的数据
    minsyz=min(syz);
    meansyz=mean(syz);
    pos=find(syz==minsyz);
    LC3(counter+1)=meansyz;
    if minsyz        Best=minsyz;
        Xp=farmpos(1);
    end
    LC4(counter+1)=Best;
    ppp=(1-Xp)+(1-q).*Xp;
    LC1(counter+1)=sum(w.*prod(ppp));
    LC2(counter+1)=sum(sum(e.*Xp));

第五步：变异

%% 第五步：变异
    for i=1:N
        if Pm>rand%是否变异由变异概率Pm控制
            AA=farmi;%取出一个个体
            POS=unidrnd(50);%随机选择变异位
            R=rand;
            Col=zeros(4,1);
            if R<0.7
                RP=randperm(4);
                Col(RP(1))=1;
            elseif R>0.9
                RP=randperm(4);
                Col(RP(1:2))=1;
            else
                RP=randperm(4);
                Col(RP(1:3))=1;
            end
            %下面是判断变异产生的新个体是否满足约束，如果不满足，此次变异无效
            AA(:,POS)=Col;
            Temp1=sum(AA,2);
            Temp2=find(Temp1>20);
            if length(Temp2)==0
                farmi=AA;
            end
        end
    end
    counter=counter+1
end

第七步：绘收敛曲线图

%第七步：绘收敛曲线图
figure(1);
plot(LC1);
xlabel('迭代次数');
ylabel('子目标1的值');
title('子目标1的收敛曲线');
figure(2);
plot(LC2);
xlabel('迭代次数');
ylabel('子目标2的值');
title('子目标2的收敛曲线');
figure(3);
plot(LC3);
xlabel('迭代次数');
ylabel('适应度函数的平均值');
title('平均适应度函数的收敛曲线');
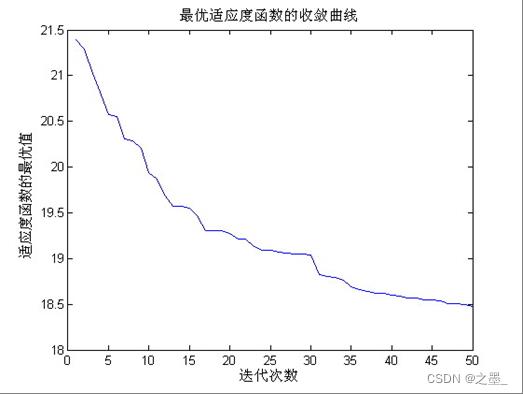
figure(4);
plot(LC4);
xlabel('迭代次数');
ylabel('适应度函数的最优值');
title('最优适应度函数的收敛曲线');

贴出一幅运行得到的收敛曲线