数字信号处理基本序列 ( 实指数序列 | 收敛序列 | 发散序列 )
Posted 韩曙亮
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数字信号处理基本序列 ( 实指数序列 | 收敛序列 | 发散序列 )相关的知识,希望对你有一定的参考价值。
文章目录
一、实指数序列
实指数序列 :
x ( n ) = a n u ( n ) x (n) = a^n u(n) x(n)=anu(n)
上述函数中 , a a a 是实数 ,
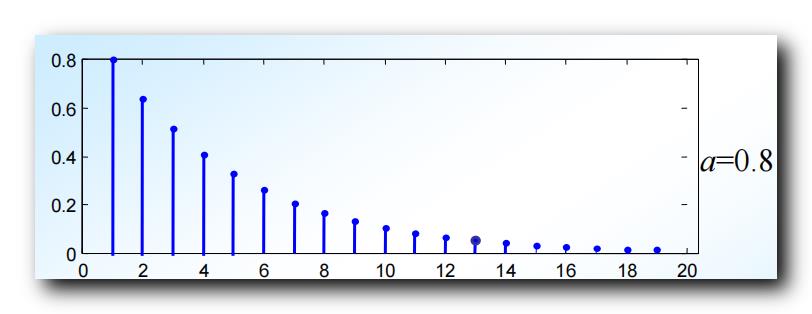
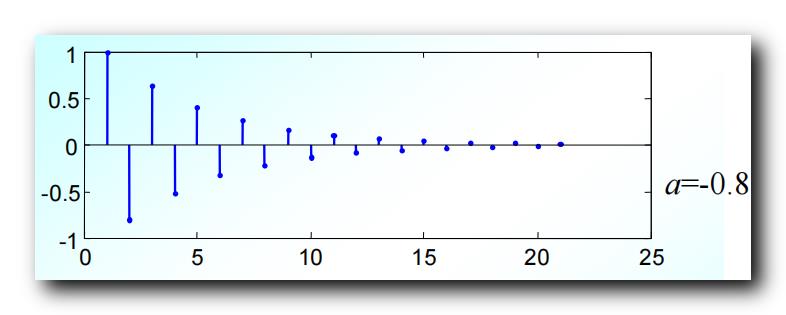
- 当 ∣ a ∣ < 1 |a| <1 ∣a∣<1 时 , x ( n ) x(n) x(n) 会随着 n n n 增大而收敛 , 是 收敛序列 ;
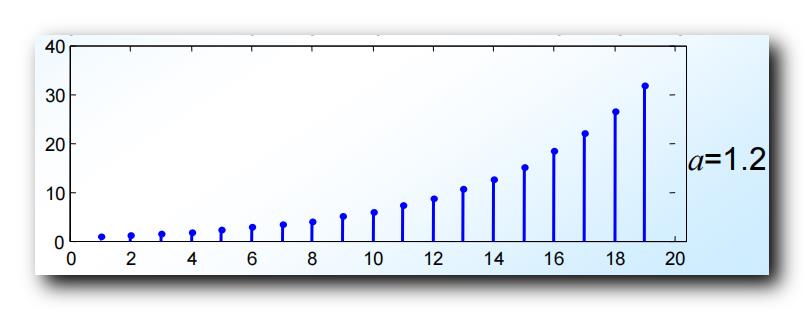
- 当 ∣ a ∣ > 1 |a| >1 ∣a∣>1 时 , x ( n ) x(n) x(n) 会随着 n n n 增大而发散 , 是 发散序列 ;
实指数序列 函数图像 如下图所示 :
∣ a ∣ < 1 |a| <1 ∣a∣<1 时 , 序列收敛 :
∣
a
∣
>
1
|a| >1
∣a∣>1 时 , 序列发散 :

以上是关于数字信号处理基本序列 ( 实指数序列 | 收敛序列 | 发散序列 )的主要内容,如果未能解决你的问题,请参考以下文章
数字信号处理傅里叶变换性质 ( 序列傅里叶变换共轭对称性质 | 序列实偶 傅里叶变换 实偶 | 序列实奇 傅里叶变换 虚奇 | 证明 “ 序列实奇 傅里叶变换 虚奇 “ )
数字信号处理序列傅里叶变换 ( 序列傅里叶变换定义详细分析 | 证明单位复指数序列正交完备性 | 序列存在傅里叶变换的性质 | 序列绝对可和 → 序列傅里叶变换一定存在 )
数字信号处理序列傅里叶变换 ( 序列傅里叶变换定义详细分析 | 证明单位复指数序列正交完备性 | 序列存在傅里叶变换的性质 | 序列绝对可和 → 序列傅里叶变换一定存在 )
数字信号处理傅里叶变换性质 ( 共轭对称与共轭反对称图像示例 | 实序列中共轭对称是偶对称 | 实序列中共轭反对称是奇对称 )
数字信号处理傅里叶变换性质 ( 序列傅里叶变换共轭对称性质示例 | 证明 原序列实部 x_R(n) 的 傅里叶变换 是 原序列傅里叶变换 的 共轭对称序列 )